三角形中位线
图片预览

文档简介
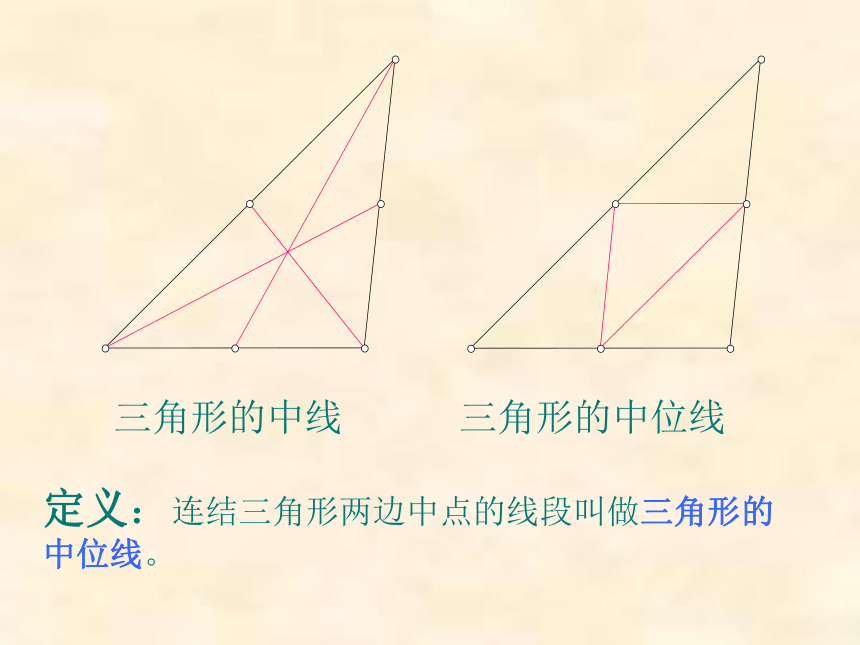
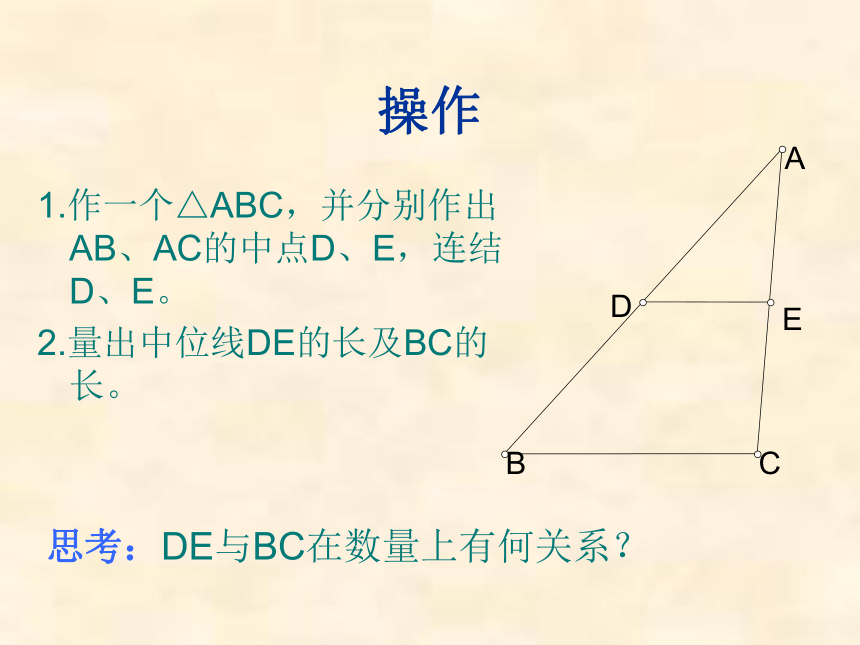
课件10张PPT。三角形的中位线上海民办明珠中学 周雷三角形的中线三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线。操作1.作一个△ABC,并分别作出AB、AC的中点D、E,连结D、E。
2.量出中位线DE的长及BC的长。
思考:DE与BC在数量上有何关系?
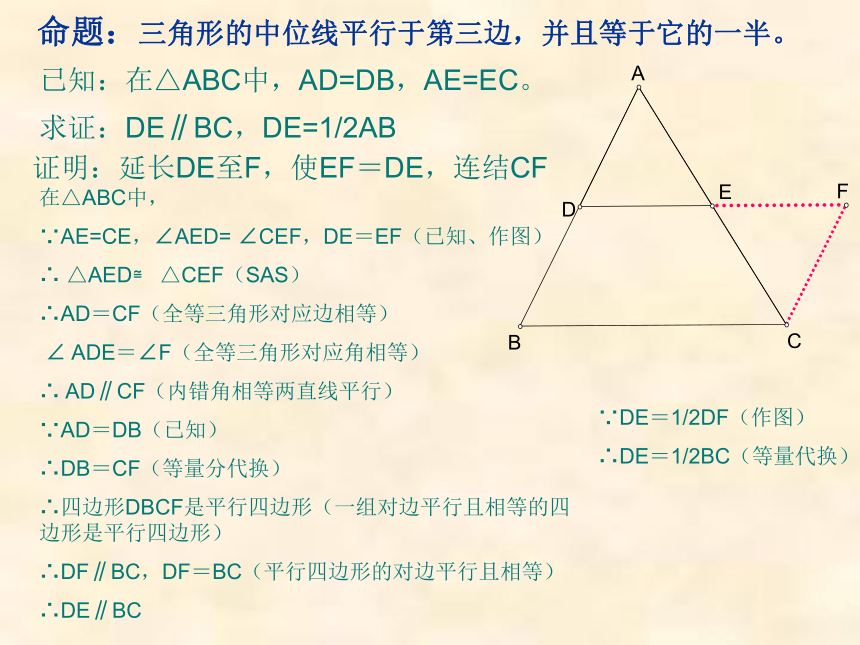
命题:三角形的中位线平行于第三边,并且等于它的一半。ABCDEF已知:在△ABC中,AD=DB,AE=EC。求证:DE∥BC,DE=1/2AB在△ABC中,
∵AE=CE,∠AED= ∠CEF,DE=EF(已知、作图)
∴ △AED≌ △CEF(SAS)
∴AD=CF(全等三角形对应边相等)
∠ ADE=∠F(全等三角形对应角相等)
∴ AD∥CF(内错角相等两直线平行)
∵AD=DB(已知)
∴DB=CF(等量分代换)
∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴DF∥BC,DF=BC(平行四边形的对边平行且相等)
∴DE∥BC证明:延长DE至F,使EF=DE,连结CF∵DE=1/2DF(作图)
∴DE=1/2BC(等量代换)
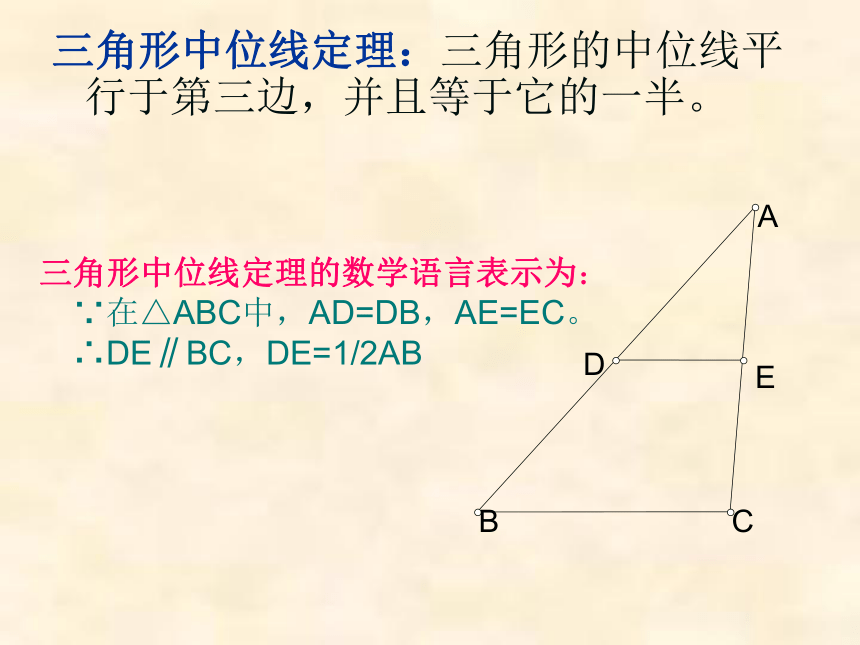
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的数学语言表示为:
∵在△ABC中,AD=DB,AE=EC。
∴DE∥BC,DE=1/2AB
练习1在△ABC中,D、E、F分别是AB、BC、CA中点,若AB=12,BC=8,CA=10,则DE=___,EF=__,FD=__。练习2在△ABC中,M、N分别是AC、BC中点,若MN=20,则AB=___。例1.已知点O是△ABC内一点,D、E、F、G分别是AO、BO、BC、AC的中点。
求证:四边形DEFG是平行四边形。证明:在△ABC中,
∵ D、E分别是AO、BO的中点(已知)
∴DE∥AB,DE=1/2AB(三角形的中位线平行于第三边,并且等于它的一半)
同理:GF∥AB, GF=1/2AB
∴DE∥GF,DE=GF
∴四边形DEFG是平行四边形(一组对边平行且相等的四边形是平行四边形)
例2、求证:顺次连结四边形各边中点所得的四边形是平行四边形。已知:E、F、G、H分别是四边形ABCD各边的中点
求证:四边形EFGH是平行四边形。思考:若连结对角线互相垂直的四边形各边的中点,所得的四边形是什么四边形,为什么?小结1.三角形中位线定义。
2.三角形中位线定理。
3.发现事物的一般规律。
2.量出中位线DE的长及BC的长。
思考:DE与BC在数量上有何关系?
命题:三角形的中位线平行于第三边,并且等于它的一半。ABCDEF已知:在△ABC中,AD=DB,AE=EC。求证:DE∥BC,DE=1/2AB在△ABC中,
∵AE=CE,∠AED= ∠CEF,DE=EF(已知、作图)
∴ △AED≌ △CEF(SAS)
∴AD=CF(全等三角形对应边相等)
∠ ADE=∠F(全等三角形对应角相等)
∴ AD∥CF(内错角相等两直线平行)
∵AD=DB(已知)
∴DB=CF(等量分代换)
∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴DF∥BC,DF=BC(平行四边形的对边平行且相等)
∴DE∥BC证明:延长DE至F,使EF=DE,连结CF∵DE=1/2DF(作图)
∴DE=1/2BC(等量代换)
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的数学语言表示为:
∵在△ABC中,AD=DB,AE=EC。
∴DE∥BC,DE=1/2AB
练习1在△ABC中,D、E、F分别是AB、BC、CA中点,若AB=12,BC=8,CA=10,则DE=___,EF=__,FD=__。练习2在△ABC中,M、N分别是AC、BC中点,若MN=20,则AB=___。例1.已知点O是△ABC内一点,D、E、F、G分别是AO、BO、BC、AC的中点。
求证:四边形DEFG是平行四边形。证明:在△ABC中,
∵ D、E分别是AO、BO的中点(已知)
∴DE∥AB,DE=1/2AB(三角形的中位线平行于第三边,并且等于它的一半)
同理:GF∥AB, GF=1/2AB
∴DE∥GF,DE=GF
∴四边形DEFG是平行四边形(一组对边平行且相等的四边形是平行四边形)
例2、求证:顺次连结四边形各边中点所得的四边形是平行四边形。已知:E、F、G、H分别是四边形ABCD各边的中点
求证:四边形EFGH是平行四边形。思考:若连结对角线互相垂直的四边形各边的中点,所得的四边形是什么四边形,为什么?小结1.三角形中位线定义。
2.三角形中位线定理。
3.发现事物的一般规律。
