梯形的中位线
图片预览

文档简介
课件19张PPT。梯形的中位线上海民办明珠中学 周雷学习目标:学习重点;探索梯形中位线的性质,并会运用性质解决有关问题。
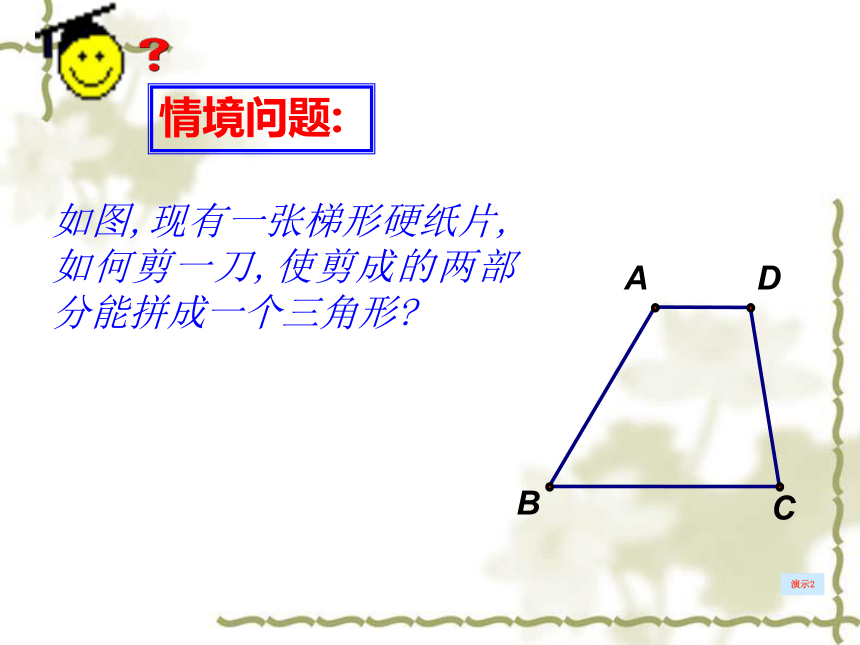
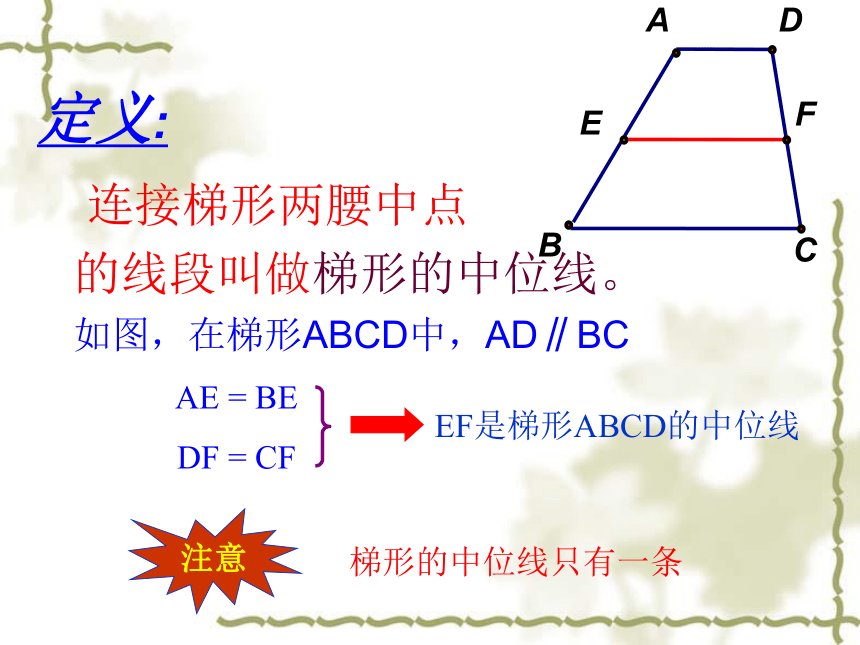
学习难点;探索、推理得出梯形中位线的性质。如图,现有一张梯形硬纸片,如何剪一刀,使剪成的两部分能拼成一个三角形?ADBC演示2情境问题:定义: 连接梯形两腰中点
的线段叫做梯形的中位线。
如图,在梯形ABCD中,AD∥BCEF是梯形ABCD的中位线AE = BE
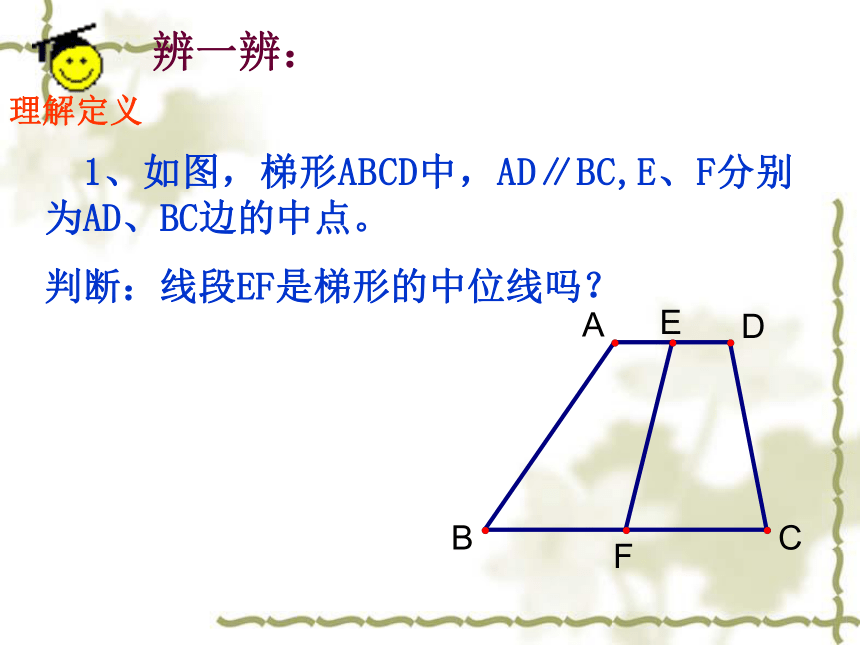
DF = CF梯形的中位线只有一条注意理解定义辨一辨: 1、如图,梯形ABCD中,AD∥BC,E、F分别为AD、BC边的中点。
判断:线段EF是梯形的中位线吗?
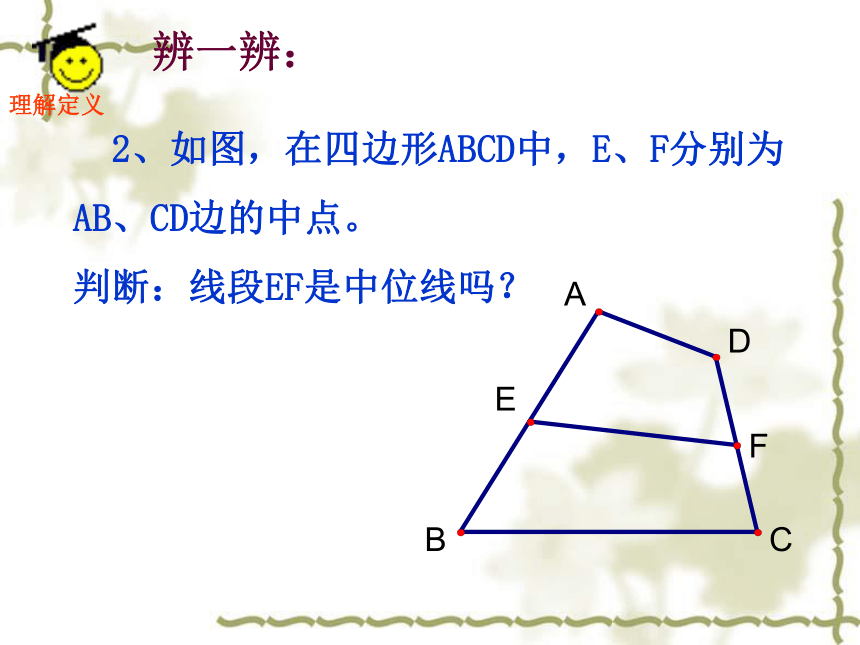
理解定义辨一辨: 2、如图,在四边形ABCD中,E、F分别为
AB、CD边的中点。
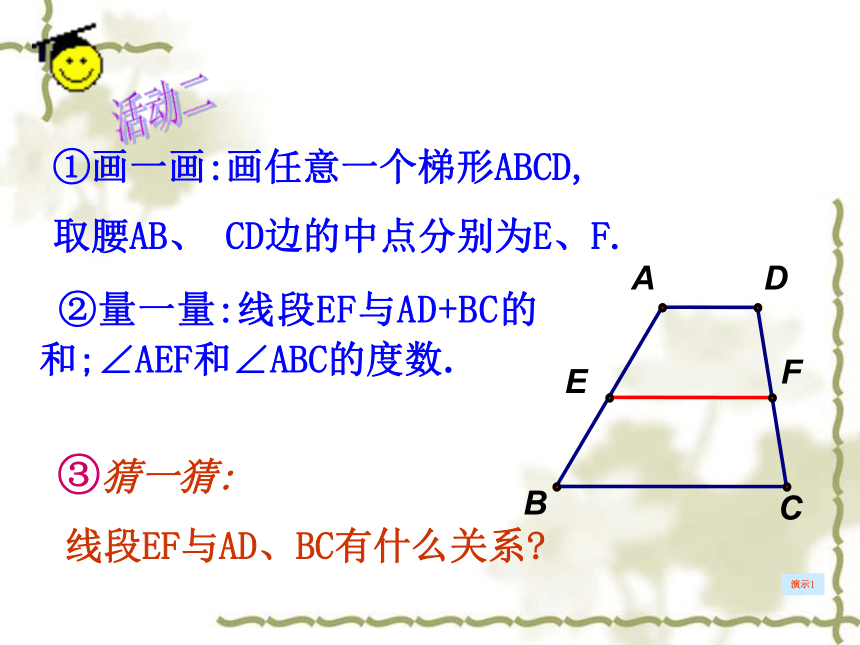
判断:线段EF是中位线吗?①画一画:画任意一个梯形ABCD,
取腰AB、 CD边的中点分别为E、F. ②量一量:线段EF与AD+BC的和;∠AEF和∠ABC的度数. ③猜一猜:
线段EF与AD、BC有什么关系?演示1活动二 梯形
中位线性质 梯形的中位线平行于两底,
并且等于两底和的一半 。已知:梯形ABCD中,AD∥BC,
AE=EB,DF=FC请说明EF∥BC
且GFEADBCEF= (AD+BC)的理由 梯形
中位线性质 梯形的中位线平行于两底,并且等于两底和的一半。FEADBC性质的符号语言:∵在梯形ABCD中,AD∥BC,AE=EB,
DF=FClbah 梯子各横木间互相平行,
且 A1A2= A2A3= A3A4= A4A5,
B1B2=B2B3= B3B4=B4B5.
已知横木A1B1=48cm,
A2 B2=44cm,
求横木A3B3、A4B4、A5B5的长。例题一、填一填 1、梯形上底长为8cm,下底长
为10cm,则中位线长为______cm.
2、梯形的上底长为8cm,中位线长为
10cm,高为6cm,则下底长为________cm;
面积为________cm2.
91260 小试牛刀3、如图,把长为8cm的长方形纸片对折,
按图中的虚线剪出一个梯形并打开,则
打开后梯形中位线的长为_____。1cm4cm5cm小试牛刀 1、一个等腰梯形的周长是80cm,且
它的中位线长与腰长相等,它的高为12cm,
这个梯形的面积是: ( )
A.60cm2 B.120cm2 C.240cm2 D.300cm2 各显身手二、选一选CABCDEFH 2.如图,在梯形ABCD中,AD∥EF ∥ GH ∥ BC,
AE=EG=GB,DF=FH=HC,AD=18, BC=32,
则EF+GH=( )
(A)48
(B)49
(C)50
(D)52ABCDEGFH各显身手C三、算一算EABCDMN如图,在△ABC中,M、N分别是AB、AC的四分之一点,BC=8cm求MN的长。ABCMN巧妙运用这节课,你有什么感受?★知道了梯形中位线的定义和性质;
★会用转化的思想来推理梯形中位线性质;
★梯形的第二种面积公式:中位线长×高
★会用梯形中位线性质解决一些数学问题。
数学是思维的体操!勇于尝试,敢于探索,我们就能学到更多,做得更好! ——与同学们共勉谢谢!再见
学习难点;探索、推理得出梯形中位线的性质。如图,现有一张梯形硬纸片,如何剪一刀,使剪成的两部分能拼成一个三角形?ADBC演示2情境问题:定义: 连接梯形两腰中点
的线段叫做梯形的中位线。
如图,在梯形ABCD中,AD∥BCEF是梯形ABCD的中位线AE = BE
DF = CF梯形的中位线只有一条注意理解定义辨一辨: 1、如图,梯形ABCD中,AD∥BC,E、F分别为AD、BC边的中点。
判断:线段EF是梯形的中位线吗?
理解定义辨一辨: 2、如图,在四边形ABCD中,E、F分别为
AB、CD边的中点。
判断:线段EF是中位线吗?①画一画:画任意一个梯形ABCD,
取腰AB、 CD边的中点分别为E、F. ②量一量:线段EF与AD+BC的和;∠AEF和∠ABC的度数. ③猜一猜:
线段EF与AD、BC有什么关系?演示1活动二 梯形
中位线性质 梯形的中位线平行于两底,
并且等于两底和的一半 。已知:梯形ABCD中,AD∥BC,
AE=EB,DF=FC请说明EF∥BC
且GFEADBCEF= (AD+BC)的理由 梯形
中位线性质 梯形的中位线平行于两底,并且等于两底和的一半。FEADBC性质的符号语言:∵在梯形ABCD中,AD∥BC,AE=EB,
DF=FClbah 梯子各横木间互相平行,
且 A1A2= A2A3= A3A4= A4A5,
B1B2=B2B3= B3B4=B4B5.
已知横木A1B1=48cm,
A2 B2=44cm,
求横木A3B3、A4B4、A5B5的长。例题一、填一填 1、梯形上底长为8cm,下底长
为10cm,则中位线长为______cm.
2、梯形的上底长为8cm,中位线长为
10cm,高为6cm,则下底长为________cm;
面积为________cm2.
91260 小试牛刀3、如图,把长为8cm的长方形纸片对折,
按图中的虚线剪出一个梯形并打开,则
打开后梯形中位线的长为_____。1cm4cm5cm小试牛刀 1、一个等腰梯形的周长是80cm,且
它的中位线长与腰长相等,它的高为12cm,
这个梯形的面积是: ( )
A.60cm2 B.120cm2 C.240cm2 D.300cm2 各显身手二、选一选CABCDEFH 2.如图,在梯形ABCD中,AD∥EF ∥ GH ∥ BC,
AE=EG=GB,DF=FH=HC,AD=18, BC=32,
则EF+GH=( )
(A)48
(B)49
(C)50
(D)52ABCDEGFH各显身手C三、算一算EABCDMN如图,在△ABC中,M、N分别是AB、AC的四分之一点,BC=8cm求MN的长。ABCMN巧妙运用这节课,你有什么感受?★知道了梯形中位线的定义和性质;
★会用转化的思想来推理梯形中位线性质;
★梯形的第二种面积公式:中位线长×高
★会用梯形中位线性质解决一些数学问题。
数学是思维的体操!勇于尝试,敢于探索,我们就能学到更多,做得更好! ——与同学们共勉谢谢!再见
