角平分线性质学案
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
《角平分线的性质》学案
学习目标:
1.初步掌握角平分线的性质和几何语言,能够进行简单的计算与证明。
2.能够从复杂图形中提炼出基本图形,体会构造基本图形是添加辅助线解题的基本原则。
3.通过实验,讨论,研究,归纳等过程,体会先猜想后推理验证的学习方法,感受学习中自主发现,探索的乐趣,培养良好的学习习惯。
学习重点:求角平分线的性质。
学习难点:角平分线的性质及应用。
【活动一】猜想结论:折纸实验
小组讨论:思考利用折纸实验,不利用画图工具,如何确定角平分线?
思考在角平分线上任意取一点P,过P向两边作垂线段,这两条垂线段的长度有什么关系?
【活动二】证明结论
已知:(如图) OC平分∠AOB, P是OC上一点,PD⊥OA,PE⊥OB
求证:PD=PE
角平分线的性质:
角的平分线上的点到角的两边的距离相等。
你能把文字语言转化成几何语言吗?
几何语言:
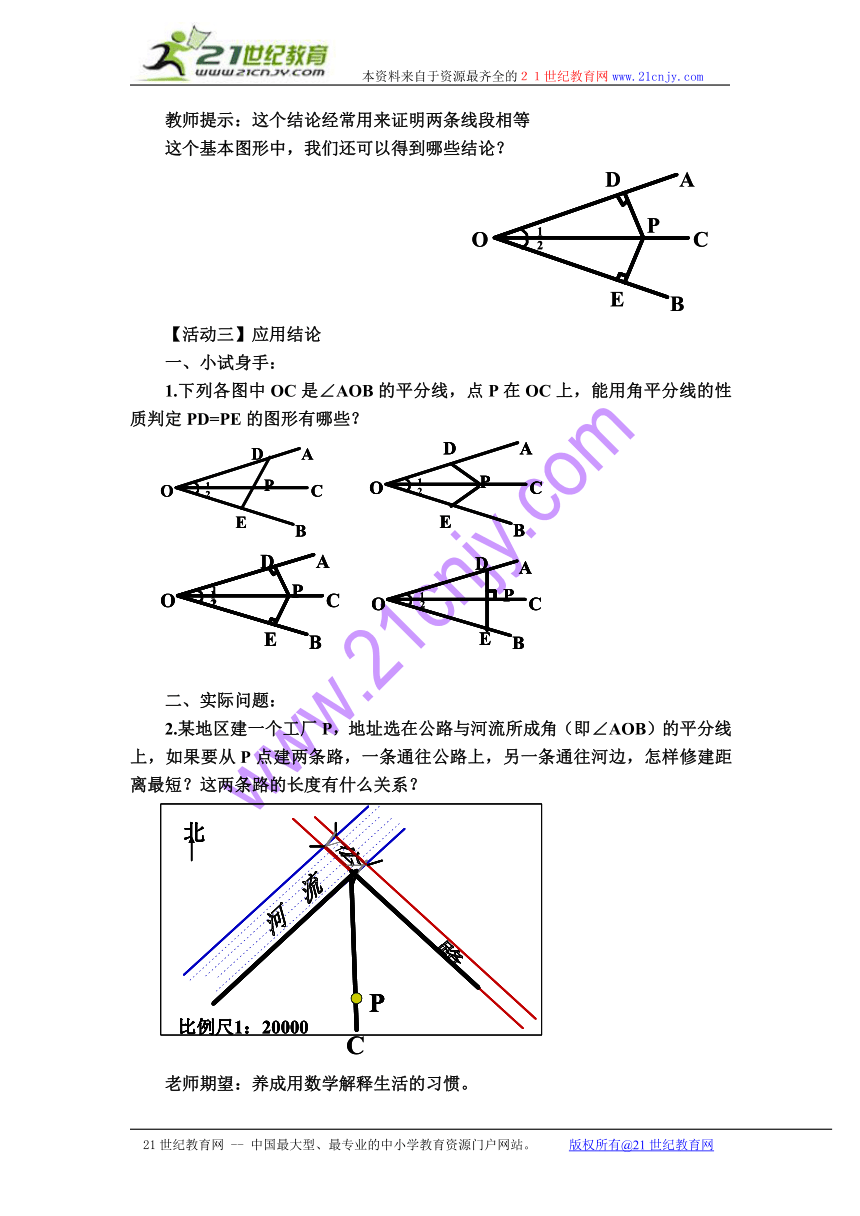
教师提示:这个结论经常用来证明两条线段相等
这个基本图形中,我们还可以得到哪些结论?
【活动三】应用结论
一、小试身手:
1.下列各图中OC是∠AOB的平分线,点P在OC上,能用角平分线的性质判定PD=PE的图形有哪些?
二、实际问题:
2.某地区建一个工厂P,地址选在公路与河流所成角(即∠AOB)的平分线上,如果要从P点建两条路,一条通往公路上,另一条通往河边,怎样修建距离最短?这两条路的长度有什么关系?
老师期望:养成用数学解释生活的习惯。
三、合作交流:
3.如图,在△ABC中,∠C=90 °,AD为∠BAC的平分线,DE⊥AB于E
(1)若BC=7,DE=3。则BD的长为 。
老师期望:从复杂图形中同学们能找出基本图形。
(2)若点F在AC边上,BD=DF,你能得到哪些结论?请说明理由。
老师期望:同学们能写出规范的证明过程。
四、动动脑筋:
4.△ABC中,∠C=90°,AD平分∠CAB,且BC=8,BD=5,
(1)点D到AB的距离为 。
(2)若AB=12,则 = 。
教师期望:同学们能够从这道题中得到些启发。
5.如图,OP平分∠AOB,AC=BD,问:和有什么关系?
五、能力提高
6.如图, 在四边形ABDF中,AD为∠BAC的平分线,BD=DF,
求证:∠B+∠F=180 °
【小结】
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
《角平分线的性质》学案
学习目标:
1.初步掌握角平分线的性质和几何语言,能够进行简单的计算与证明。
2.能够从复杂图形中提炼出基本图形,体会构造基本图形是添加辅助线解题的基本原则。
3.通过实验,讨论,研究,归纳等过程,体会先猜想后推理验证的学习方法,感受学习中自主发现,探索的乐趣,培养良好的学习习惯。
学习重点:求角平分线的性质。
学习难点:角平分线的性质及应用。
【活动一】猜想结论:折纸实验
小组讨论:思考利用折纸实验,不利用画图工具,如何确定角平分线?
思考在角平分线上任意取一点P,过P向两边作垂线段,这两条垂线段的长度有什么关系?
【活动二】证明结论
已知:(如图) OC平分∠AOB, P是OC上一点,PD⊥OA,PE⊥OB
求证:PD=PE
角平分线的性质:
角的平分线上的点到角的两边的距离相等。
你能把文字语言转化成几何语言吗?
几何语言:
教师提示:这个结论经常用来证明两条线段相等
这个基本图形中,我们还可以得到哪些结论?
【活动三】应用结论
一、小试身手:
1.下列各图中OC是∠AOB的平分线,点P在OC上,能用角平分线的性质判定PD=PE的图形有哪些?
二、实际问题:
2.某地区建一个工厂P,地址选在公路与河流所成角(即∠AOB)的平分线上,如果要从P点建两条路,一条通往公路上,另一条通往河边,怎样修建距离最短?这两条路的长度有什么关系?
老师期望:养成用数学解释生活的习惯。
三、合作交流:
3.如图,在△ABC中,∠C=90 °,AD为∠BAC的平分线,DE⊥AB于E
(1)若BC=7,DE=3。则BD的长为 。
老师期望:从复杂图形中同学们能找出基本图形。
(2)若点F在AC边上,BD=DF,你能得到哪些结论?请说明理由。
老师期望:同学们能写出规范的证明过程。
四、动动脑筋:
4.△ABC中,∠C=90°,AD平分∠CAB,且BC=8,BD=5,
(1)点D到AB的距离为 。
(2)若AB=12,则 = 。
教师期望:同学们能够从这道题中得到些启发。
5.如图,OP平分∠AOB,AC=BD,问:和有什么关系?
五、能力提高
6.如图, 在四边形ABDF中,AD为∠BAC的平分线,BD=DF,
求证:∠B+∠F=180 °
【小结】
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
