2011版高三数学一轮精品复习学案命题及其关系
文档属性
| 名称 | 2011版高三数学一轮精品复习学案命题及其关系 |

|
|
| 格式 | rar | ||
| 文件大小 | 191.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-02 00:00:00 | ||
图片预览




文档简介
2011版高三数学一轮精品复习学案:第一章集合与常用逻辑用语
第二节 命题及其关系、充分条件与必要条件
【高考目标定位】
一、考纲点击
1、理解命题的概念;
2、了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系;
3、理解必要条件、充分条件与充要条件的意义。
二、热点、难点提示
1、充分必要条件的判断和四种命题及其关系是本节考查的热点;
2、多以选择题、填空题的形式出现,由于知识载体丰富,具有较强的综合性,属于中、低档题目;有时也在解答题中出现,考查对概念的理解与应用,难度不会太大。
【考纲知识梳理】
1、命题
用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题。
2、四种命题及其关系
(1)四种命题
命题 表述形式
原命题 若p,则q
逆命题 若q,则p
否命题 若,则
逆否命题 若,则
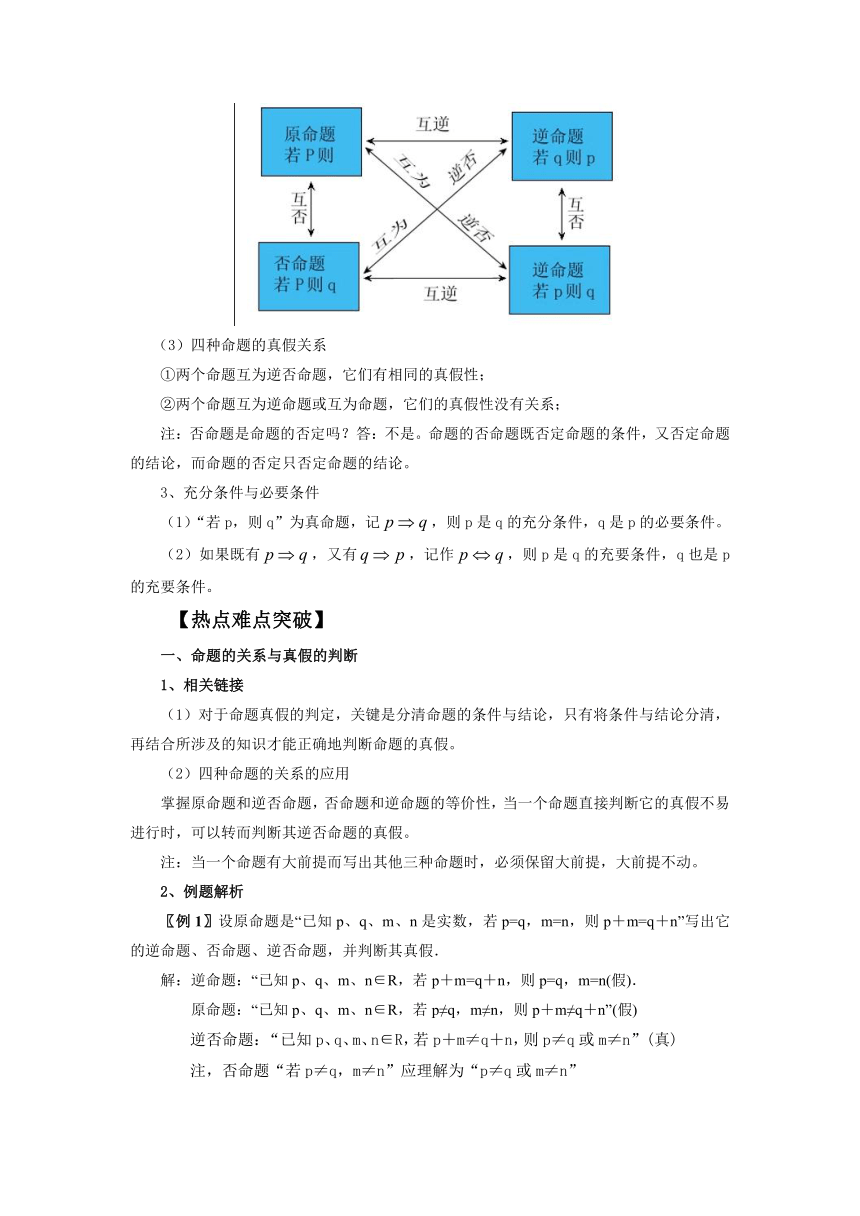
(2)四种命题间的相互关系
(3)四种命题的真假关系
①两个命题互为逆否命题,它们有相同的真假性;
②两个命题互为逆命题或互为命题,它们的真假性没有关系;
注:否命题是命题的否定吗?答:不是。命题的否命题既否定命题的条件,又否定命题的结论,而命题的否定只否定命题的结论。
3、充分条件与必要条件
(1)“若p,则q”为真命题,记,则p是q的充分条件,q是p的必要条件。
(2)如果既有,又有,记作,则p是q的充要条件,q也是p的充要条件。
【热点难点突破】
一、命题的关系与真假的判断
1、相关链接
(1)对于命题真假的判定,关键是分清命题的条件与结论,只有将条件与结论分清,再结合所涉及的知识才能正确地判断命题的真假。
(2)四种命题的关系的应用
掌握原命题和逆否命题,否命题和逆命题的等价性,当一个命题直接判断它的真假不易进行时,可以转而判断其逆否命题的真假。
注:当一个命题有大前提而写出其他三种命题时,必须保留大前提,大前提不动。
2、例题解析
〖例1〗设原命题是“已知p、q、m、n是实数,若p=q,m=n,则p+m=q+n”写出它的逆命题、否命题、逆否命题,并判断其真假.
解:逆命题:“已知p、q、m、n∈R,若p+m=q+n,则p=q,m=n(假).
原命题:“已知p、q、m、n∈R,若p≠q,m≠n,则p+m≠q+n”(假)
逆否命题:“已知p、q、m、n∈R,若p+m≠q+n,则p≠q或m≠n”(真)
注,否命题“若p≠q,m≠n”应理解为“p≠q或m≠n”
即是指:①p≠q,但m=n,②p=q但m≠n,而不含p≠q且m≠n.因为原命题中的条件:“若p=q,m=n.”应理解为“若p=q且m=n,”而这一语句的否定应该是“p≠q或m≠n”.
〖例2〗写出下列命题的逆命题、否命题、逆否命题并判断其真假。
(1)等底等高的两个三角形是全等三角形;
(2)若ab=0,则a=0或b=0。
解:(1)逆命题:若两个三角形全等,则这两个三角形等底等高。真命题;
否命题:若两个三角形不等底或不等高,则这两个三角形不全等。真命题;
逆否命题:若两个三角形不全等,则这两个三角形不等或不等高。假命题。
(2)逆命题:若a=0或b=0,则ab=0。真命题;
否命题:若ab≠0,则a≠0且b≠0.真命题;
逆否命题:若a≠0且b≠0,则ab≠0。真命题。
二、充分条件与必要条件的判定
1、相关链接
(1)利用定义判断
①若,则p是q的充分条件;
注:“p是q的充分条件”是指有p就有q,但无p也可能有q.如“两个三角形全等”是“两个三角形面积相等”的一个充分(不必要)条件,但无“两个三角形全等”也可推出“两个三角形面积相等”,如“两个三角形同底等高”就又是“两个三角形面积相等”的另一个充分(不必要)条件.
②若,则p是q的必要条件;
注:ⅰ “q是p的必要条件”是指有q才能有p,但有q未必有p.如,一个偶数未必能被6整除(q:为偶数,p:能被6整除).
ⅱ
③若且,p是q的充要条件;
④
⑤p是q的必要而不充分条件.
⑥
(2)利用集合判断
记条件p、q对应的集合分别为A、B,则:
若
若,则p是q的充分不必要条件;
若
若,则p是q的必要不充分条件;
若A=B,则p是q的充要条件;
注:p与q之间的关系的方向性,充分条件与必要条件方向正好相反,不要混淆。
2、例题解析
〖例1〗 “”是“直线相互垂直”的( )
A.充分必要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
答案:B;
解析:当时两直线斜率乘积为从而可得两直线垂直,当时两直线一条斜率为0一条斜率不存在,但两直线仍然垂直.因此是题目中给出的两条直线垂直的充分但不必要条件。
注:对于两条直线垂直的充要条件①都存在时②中有一个不存在另一个为零对于②这种情况多数考生容易忽略。
〖例2〗指出下列各组命题中,p是q的什么条件?
(1)p:a,b不全是偶数;q:a+b不是偶数.
(2)p:a,b,c∈R,b2-4ac≥0;q:关于x的二次方程ax2+bx+c=0有实数根.
(3)p:两个三角形相似;q:两个三角形等积.
解析: (1)a,b不全是偶数,即a,b二数“一奇一偶”或“同奇”,所以a
所以p是q的既不充分又不必要条件.
三、充要条件的证明
〖例〗(12分)求证方程ax2+2x+1=0有且只有一个负数根的充要条件为a≤0或a=1.
分析:(1)讨论a 的不同取值情况;
(2)利用根的判别式求a的取值范围.
解答:充分性:当a=0时,方程变为2x+1=0,其根为x=,方程只有一个负根;
当a=1时,方程为x2+2x+1=0.其根为x=-1,
方程只有一个负根。
当a<0时,Δ=4(1-a)>0,方程有两个不相等的根,且<0,方程有一正一负根。
必要性:若方程ax2+2x+1=0有且仅有一个负根。
当a=0时,适合条件。
当a≠0时,方程ax2+2x+1=0有实根,
则Δ=4(1-a)≥0,∴a≤1,
当a=1时,方程有一个负根x=-1.
若方程有且仅有一负根,则 ∴a<0
综上方程ax2+2x+1=0有且仅有一负根的充要条件为a≤0或a=1
注:(1)条件已知证明结论成立是充分性,结论已知证明条件成立是必要性;
(2)证明分为两个环节,一是充分性;二是必要性。证明时,不要认为它是推理过程的“双向书写”,而应该进行由条件到结论,由结论到条件下的两次证明;
(3)证明条件时易出现必要性与充分性混淆的情形,这就要分清哪是条件,哪是结论。
【感悟高考真题】
〖例1〗(2009浙江理)已知是实数,则“且”是“且”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:C
解析:对于“且”可以推出“且”,反之也是成立的
〖例2〗5.(2009浙江理)已知是实数,则“且”是“且”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:C
解析:对于“且”可以推出“且”,反之也是成立的
〖例3〗(2009浙江文)“”是“”的( A )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
A 【命题意图】本小题主要考查了命题的基本关系,题中的设问通过对不等关系的分析,考查了命题的概念和对于命题概念的理解程度
【解析】对于“”“”;反之不一定成立,因此“”是“”的充分而不必要条件.
〖例4〗16.(2009安徽卷文)“”是“且”的
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 既不充分也不必要条件
解析:易得时必有.若时,则可能有,选A。
【答案】A
〖例5〗19.(2009天津卷文)设的
A 充分不必要条件 B 必要不充分条件 C充要条件 D既不充分也不必要条件
【答案】A
解析:(本试题考察了充分条件的判定以及一元高次方程的求解问题。考查逻辑推理能力。)
因为,显然条件的集合小,结论表示的集合大,由集合的包含关系,我们不难得到结论。
〖例6〗(2010上海文数)16.“”是“”成立的 [答]( A )
(A)充分不必要条件. (B)必要不充分条件.
(C)充分条件. (D)既不充分也不必要条件.
解析:,所以充分;但反之不成立,如
〖例7〗(2010湖南文数)2. 下列命题中的假命题是
A. B.
C. D.
【答案】C
【解析】对于C选项x=1时,,故选C
〖例8〗(2010陕西文数)6.“a>0”是“>0”的 [A]
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
解析:本题考查充要条件的判断
, a>0”是“>0”的充分不必要条件
〖例9〗(2010浙江文数)(6)设0<x<,则“x sin2x<1”是“x sinx<1”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
解析:因为0<x<,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
【考点精题精练】
(1)(黑龙江庆安三中·2010届高三月考)3.对于非零向量“”是“”的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
(2)(湖北部分高中·2010届高三联考)4. 若不等式
的取值范围是( )
A. B. C. D.
(3)(湖北黄冈中学·2010届高三月考) 4.记等比数列的公比为,则“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4答案:D
解析:可以借助反例说明:①如数列: 公比为,但不是增数列;
②如数列: 是增数列,但是公比为.
(4)(安徽·合肥168中高三段考(理)) 2已知条件:,条件:,且是的充分不必要条件,则的取值范围可以是( A )
A.; B.; C.; D.;
答案:A
(5)(安徽·合肥168中高三段考(理))2.“”是 “”的 ( B )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案:B
(6)(黑龙江省双鸭山一中·2010届高三期中考试(文))11. 已知,。若p是q的充分不必要条件,则实数a的取值范围是( C )
(A) (B) (C) (D)
(7)(湖北同升湖实验学校·2010届高三月考(文))6.已知命题:不等式的解集为R;命题:为减函数.
则是成立的( B )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
(8)已知,,,为实数,且>.则“>”是“->-”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
【解析】显然,充分性不成立.又,若->-和>都成立,则同向不等式相加得>
即由“->-”“>”
(9)是“实系数一元二次方程有虚根”的
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)既不充分也不必要条件
【答案】A
解析:△=-4<0时,-2<<2,因为是“-2<<2”的必要不充分条件,故选A
(10)下列命题中不成立的命题是 ( C )
(A) 若则a=b=0.
(B) 等腰三角形有两个角相等.
(C) 关于x的方程ax2+bx+c=0中,若b2-4ac>0则方程有两个不等实根.
(D) 菱形既是轴对称图形,又是中心对称图形.
(11)x≠0是xy≠0的 ( B )
(A) 充要条件 (B) 必要而不充分条件
(C) 充分而不必要条件 (D) 既不充分也不必要条件
(12)下列说法中正确的是 ( C )
(A) x>4是x≥3的必要而不充分条件. (B) a2>b2是|a|>|b|的充分而不必要条件.
(C) A∪B=B的充要条件是. (D) ab≥0是的充要条件.
二、填空题
(1)(湖北同升湖实验学校·2010届高三月考(理))10.若不等式成立的充分不必要条件是,则实数的取值范围是
(2)如果是pq是真命题,那么q是p的____充分__条件.
(3)p:平行四边形是轴对称图形.则p的否定命题p是:_平行四边形不都是轴对称图形__.
(4)命题pq的逆否命题是___qp__.
三、解答题
(1)写出方程:ax2+bx+c=0(a<0)有两个正根的充要条件.
解:要使方程ax2+bx+c=0(a<0=有两个正根.
b2≥2ac且b>0,c<0.
(2)设方程x2-5x+3+a=0在区间(1,3)上有实根,求实数a的取值范围.
解答:
方法1:其充要条件是
方法2:利用函数思想和数形结合思想充要条件
方法3:原命题在区间(1,3)上求函数a=-x2+5x-3的值域.
第二节 命题及其关系、充分条件与必要条件
【高考目标定位】
一、考纲点击
1、理解命题的概念;
2、了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系;
3、理解必要条件、充分条件与充要条件的意义。
二、热点、难点提示
1、充分必要条件的判断和四种命题及其关系是本节考查的热点;
2、多以选择题、填空题的形式出现,由于知识载体丰富,具有较强的综合性,属于中、低档题目;有时也在解答题中出现,考查对概念的理解与应用,难度不会太大。
【考纲知识梳理】
1、命题
用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题。
2、四种命题及其关系
(1)四种命题
命题 表述形式
原命题 若p,则q
逆命题 若q,则p
否命题 若,则
逆否命题 若,则
(2)四种命题间的相互关系
(3)四种命题的真假关系
①两个命题互为逆否命题,它们有相同的真假性;
②两个命题互为逆命题或互为命题,它们的真假性没有关系;
注:否命题是命题的否定吗?答:不是。命题的否命题既否定命题的条件,又否定命题的结论,而命题的否定只否定命题的结论。
3、充分条件与必要条件
(1)“若p,则q”为真命题,记,则p是q的充分条件,q是p的必要条件。
(2)如果既有,又有,记作,则p是q的充要条件,q也是p的充要条件。
【热点难点突破】
一、命题的关系与真假的判断
1、相关链接
(1)对于命题真假的判定,关键是分清命题的条件与结论,只有将条件与结论分清,再结合所涉及的知识才能正确地判断命题的真假。
(2)四种命题的关系的应用
掌握原命题和逆否命题,否命题和逆命题的等价性,当一个命题直接判断它的真假不易进行时,可以转而判断其逆否命题的真假。
注:当一个命题有大前提而写出其他三种命题时,必须保留大前提,大前提不动。
2、例题解析
〖例1〗设原命题是“已知p、q、m、n是实数,若p=q,m=n,则p+m=q+n”写出它的逆命题、否命题、逆否命题,并判断其真假.
解:逆命题:“已知p、q、m、n∈R,若p+m=q+n,则p=q,m=n(假).
原命题:“已知p、q、m、n∈R,若p≠q,m≠n,则p+m≠q+n”(假)
逆否命题:“已知p、q、m、n∈R,若p+m≠q+n,则p≠q或m≠n”(真)
注,否命题“若p≠q,m≠n”应理解为“p≠q或m≠n”
即是指:①p≠q,但m=n,②p=q但m≠n,而不含p≠q且m≠n.因为原命题中的条件:“若p=q,m=n.”应理解为“若p=q且m=n,”而这一语句的否定应该是“p≠q或m≠n”.
〖例2〗写出下列命题的逆命题、否命题、逆否命题并判断其真假。
(1)等底等高的两个三角形是全等三角形;
(2)若ab=0,则a=0或b=0。
解:(1)逆命题:若两个三角形全等,则这两个三角形等底等高。真命题;
否命题:若两个三角形不等底或不等高,则这两个三角形不全等。真命题;
逆否命题:若两个三角形不全等,则这两个三角形不等或不等高。假命题。
(2)逆命题:若a=0或b=0,则ab=0。真命题;
否命题:若ab≠0,则a≠0且b≠0.真命题;
逆否命题:若a≠0且b≠0,则ab≠0。真命题。
二、充分条件与必要条件的判定
1、相关链接
(1)利用定义判断
①若,则p是q的充分条件;
注:“p是q的充分条件”是指有p就有q,但无p也可能有q.如“两个三角形全等”是“两个三角形面积相等”的一个充分(不必要)条件,但无“两个三角形全等”也可推出“两个三角形面积相等”,如“两个三角形同底等高”就又是“两个三角形面积相等”的另一个充分(不必要)条件.
②若,则p是q的必要条件;
注:ⅰ “q是p的必要条件”是指有q才能有p,但有q未必有p.如,一个偶数未必能被6整除(q:为偶数,p:能被6整除).
ⅱ
③若且,p是q的充要条件;
④
⑤p是q的必要而不充分条件.
⑥
(2)利用集合判断
记条件p、q对应的集合分别为A、B,则:
若
若,则p是q的充分不必要条件;
若
若,则p是q的必要不充分条件;
若A=B,则p是q的充要条件;
注:p与q之间的关系的方向性,充分条件与必要条件方向正好相反,不要混淆。
2、例题解析
〖例1〗 “”是“直线相互垂直”的( )
A.充分必要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
答案:B;
解析:当时两直线斜率乘积为从而可得两直线垂直,当时两直线一条斜率为0一条斜率不存在,但两直线仍然垂直.因此是题目中给出的两条直线垂直的充分但不必要条件。
注:对于两条直线垂直的充要条件①都存在时②中有一个不存在另一个为零对于②这种情况多数考生容易忽略。
〖例2〗指出下列各组命题中,p是q的什么条件?
(1)p:a,b不全是偶数;q:a+b不是偶数.
(2)p:a,b,c∈R,b2-4ac≥0;q:关于x的二次方程ax2+bx+c=0有实数根.
(3)p:两个三角形相似;q:两个三角形等积.
解析: (1)a,b不全是偶数,即a,b二数“一奇一偶”或“同奇”,所以a
所以p是q的既不充分又不必要条件.
三、充要条件的证明
〖例〗(12分)求证方程ax2+2x+1=0有且只有一个负数根的充要条件为a≤0或a=1.
分析:(1)讨论a 的不同取值情况;
(2)利用根的判别式求a的取值范围.
解答:充分性:当a=0时,方程变为2x+1=0,其根为x=,方程只有一个负根;
当a=1时,方程为x2+2x+1=0.其根为x=-1,
方程只有一个负根。
当a<0时,Δ=4(1-a)>0,方程有两个不相等的根,且<0,方程有一正一负根。
必要性:若方程ax2+2x+1=0有且仅有一个负根。
当a=0时,适合条件。
当a≠0时,方程ax2+2x+1=0有实根,
则Δ=4(1-a)≥0,∴a≤1,
当a=1时,方程有一个负根x=-1.
若方程有且仅有一负根,则 ∴a<0
综上方程ax2+2x+1=0有且仅有一负根的充要条件为a≤0或a=1
注:(1)条件已知证明结论成立是充分性,结论已知证明条件成立是必要性;
(2)证明分为两个环节,一是充分性;二是必要性。证明时,不要认为它是推理过程的“双向书写”,而应该进行由条件到结论,由结论到条件下的两次证明;
(3)证明条件时易出现必要性与充分性混淆的情形,这就要分清哪是条件,哪是结论。
【感悟高考真题】
〖例1〗(2009浙江理)已知是实数,则“且”是“且”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:C
解析:对于“且”可以推出“且”,反之也是成立的
〖例2〗5.(2009浙江理)已知是实数,则“且”是“且”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:C
解析:对于“且”可以推出“且”,反之也是成立的
〖例3〗(2009浙江文)“”是“”的( A )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
A 【命题意图】本小题主要考查了命题的基本关系,题中的设问通过对不等关系的分析,考查了命题的概念和对于命题概念的理解程度
【解析】对于“”“”;反之不一定成立,因此“”是“”的充分而不必要条件.
〖例4〗16.(2009安徽卷文)“”是“且”的
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 既不充分也不必要条件
解析:易得时必有.若时,则可能有,选A。
【答案】A
〖例5〗19.(2009天津卷文)设的
A 充分不必要条件 B 必要不充分条件 C充要条件 D既不充分也不必要条件
【答案】A
解析:(本试题考察了充分条件的判定以及一元高次方程的求解问题。考查逻辑推理能力。)
因为,显然条件的集合小,结论表示的集合大,由集合的包含关系,我们不难得到结论。
〖例6〗(2010上海文数)16.“”是“”成立的 [答]( A )
(A)充分不必要条件. (B)必要不充分条件.
(C)充分条件. (D)既不充分也不必要条件.
解析:,所以充分;但反之不成立,如
〖例7〗(2010湖南文数)2. 下列命题中的假命题是
A. B.
C. D.
【答案】C
【解析】对于C选项x=1时,,故选C
〖例8〗(2010陕西文数)6.“a>0”是“>0”的 [A]
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
解析:本题考查充要条件的判断
, a>0”是“>0”的充分不必要条件
〖例9〗(2010浙江文数)(6)设0<x<,则“x sin2x<1”是“x sinx<1”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
解析:因为0<x<,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
【考点精题精练】
(1)(黑龙江庆安三中·2010届高三月考)3.对于非零向量“”是“”的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
(2)(湖北部分高中·2010届高三联考)4. 若不等式
的取值范围是( )
A. B. C. D.
(3)(湖北黄冈中学·2010届高三月考) 4.记等比数列的公比为,则“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4答案:D
解析:可以借助反例说明:①如数列: 公比为,但不是增数列;
②如数列: 是增数列,但是公比为.
(4)(安徽·合肥168中高三段考(理)) 2已知条件:,条件:,且是的充分不必要条件,则的取值范围可以是( A )
A.; B.; C.; D.;
答案:A
(5)(安徽·合肥168中高三段考(理))2.“”是 “”的 ( B )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案:B
(6)(黑龙江省双鸭山一中·2010届高三期中考试(文))11. 已知,。若p是q的充分不必要条件,则实数a的取值范围是( C )
(A) (B) (C) (D)
(7)(湖北同升湖实验学校·2010届高三月考(文))6.已知命题:不等式的解集为R;命题:为减函数.
则是成立的( B )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
(8)已知,,,为实数,且>.则“>”是“->-”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
【解析】显然,充分性不成立.又,若->-和>都成立,则同向不等式相加得>
即由“->-”“>”
(9)是“实系数一元二次方程有虚根”的
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)既不充分也不必要条件
【答案】A
解析:△=-4<0时,-2<<2,因为是“-2<<2”的必要不充分条件,故选A
(10)下列命题中不成立的命题是 ( C )
(A) 若则a=b=0.
(B) 等腰三角形有两个角相等.
(C) 关于x的方程ax2+bx+c=0中,若b2-4ac>0则方程有两个不等实根.
(D) 菱形既是轴对称图形,又是中心对称图形.
(11)x≠0是xy≠0的 ( B )
(A) 充要条件 (B) 必要而不充分条件
(C) 充分而不必要条件 (D) 既不充分也不必要条件
(12)下列说法中正确的是 ( C )
(A) x>4是x≥3的必要而不充分条件. (B) a2>b2是|a|>|b|的充分而不必要条件.
(C) A∪B=B的充要条件是. (D) ab≥0是的充要条件.
二、填空题
(1)(湖北同升湖实验学校·2010届高三月考(理))10.若不等式成立的充分不必要条件是,则实数的取值范围是
(2)如果是pq是真命题,那么q是p的____充分__条件.
(3)p:平行四边形是轴对称图形.则p的否定命题p是:_平行四边形不都是轴对称图形__.
(4)命题pq的逆否命题是___qp__.
三、解答题
(1)写出方程:ax2+bx+c=0(a<0)有两个正根的充要条件.
解:要使方程ax2+bx+c=0(a<0=有两个正根.
b2≥2ac且b>0,c<0.
(2)设方程x2-5x+3+a=0在区间(1,3)上有实根,求实数a的取值范围.
解答:
方法1:其充要条件是
方法2:利用函数思想和数形结合思想充要条件
方法3:原命题在区间(1,3)上求函数a=-x2+5x-3的值域.
