人教B版选修1-1椭圆的标准方程
文档属性
| 名称 | 人教B版选修1-1椭圆的标准方程 |

|
|
| 格式 | rar | ||
| 文件大小 | 106.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-03 00:00:00 | ||
图片预览





文档简介
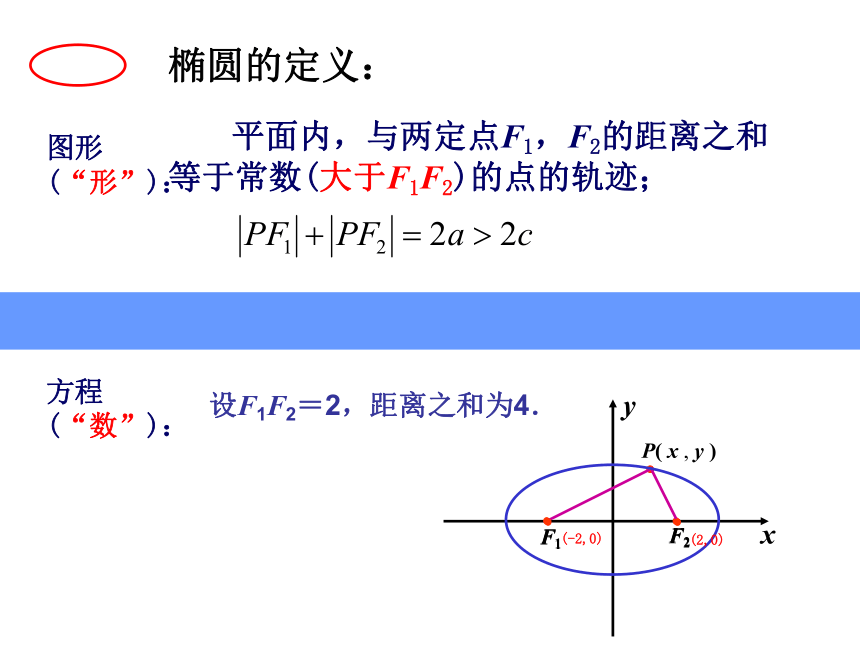
课件14张PPT。椭圆的标准方程第一课时椭圆的定义:
平面内,与两定点F1,F2的距离之和等于常数(大于F1F2)的点的轨迹;图形 (“形”):方程 (“数”):设F1F2=2,距离之和为4.(-2,0)(2,0)xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立平面直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设F1F=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足│PF1┃
+│PF2 │为定值,设为2a,
则2a>2cO标准方程的推导b2x2+a2y2=a2b2焦点在x轴上:
焦点在y轴上:
练习:判定下列椭圆的焦点在哪个坐标轴上,并指明a2、b2,写出焦点坐标 答:在 x轴。(-3,0)和(3,0) 答:在 y 轴。(0,-5)和(0,5) 答:在y 轴。(0,-1)和(0,1)判断椭圆标准方程的焦点在哪个轴上的准则:
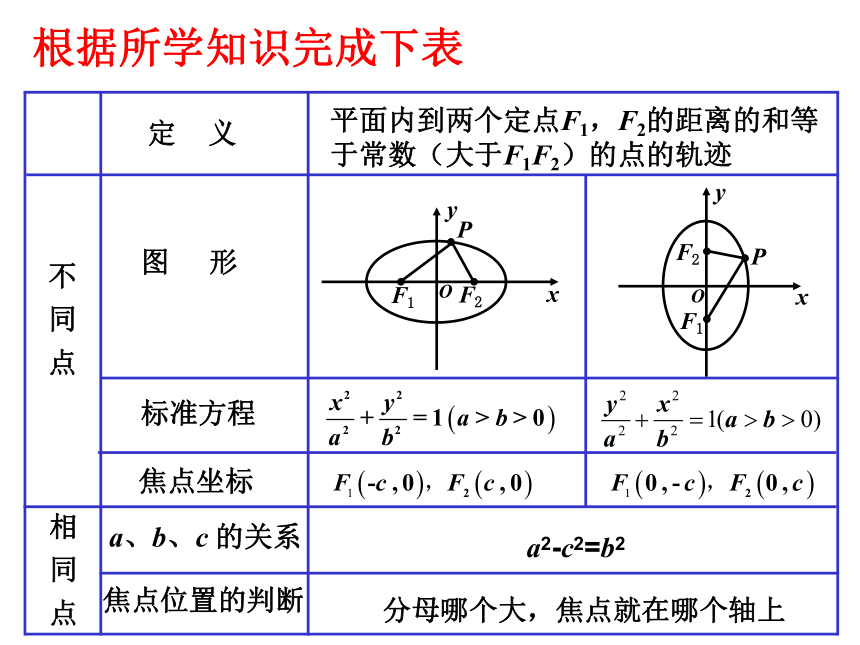
焦点在分母大的那个轴上1、2、3、分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹根据所学知识完成下表a2-c2=b2例1 : 已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.解:以两焦点F1、F2所在直线为x轴,线段F1F2的垂直平分线为
y 轴,建立如图所示的直角坐标系xOy,则这个椭圆的标准
方程可设为根据题意有即因此,这个椭圆的标准方程为例2、写出适合下列条件的椭圆的标准方程 (1) a =4,b=1,焦点在 x 轴上;
(2) a =4,b=1,焦点在坐标轴上;
(3) 两个焦点的坐标是( 0 ,-2)和( 0 ,2),并且经
过点P( -1.5 ,2.5).解: 因为椭圆的焦点在y轴上,
设它的标准方程为 ∵ c=2,且 c2= a2 - b2 ∴ 4= a2 - b2 ……①(法一)(法二) 因为椭圆的焦点在y轴上,所以设它的
标准方程为由椭圆的定义知,所以所求椭圆的标准方程为课堂小结:分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹a2-c2=b22、求椭圆的标准方程(常用待定系数法)
(1)定位
(2)定量
平面内,与两定点F1,F2的距离之和等于常数(大于F1F2)的点的轨迹;图形 (“形”):方程 (“数”):设F1F2=2,距离之和为4.(-2,0)(2,0)xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立平面直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设F1F=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足│PF1┃
+│PF2 │为定值,设为2a,
则2a>2cO标准方程的推导b2x2+a2y2=a2b2焦点在x轴上:
焦点在y轴上:
练习:判定下列椭圆的焦点在哪个坐标轴上,并指明a2、b2,写出焦点坐标 答:在 x轴。(-3,0)和(3,0) 答:在 y 轴。(0,-5)和(0,5) 答:在y 轴。(0,-1)和(0,1)判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上1、2、3、分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹根据所学知识完成下表a2-c2=b2例1 : 已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.解:以两焦点F1、F2所在直线为x轴,线段F1F2的垂直平分线为
y 轴,建立如图所示的直角坐标系xOy,则这个椭圆的标准
方程可设为根据题意有即因此,这个椭圆的标准方程为例2、写出适合下列条件的椭圆的标准方程 (1) a =4,b=1,焦点在 x 轴上;
(2) a =4,b=1,焦点在坐标轴上;
(3) 两个焦点的坐标是( 0 ,-2)和( 0 ,2),并且经
过点P( -1.5 ,2.5).解: 因为椭圆的焦点在y轴上,
设它的标准方程为 ∵ c=2,且 c2= a2 - b2 ∴ 4= a2 - b2 ……①(法一)(法二) 因为椭圆的焦点在y轴上,所以设它的
标准方程为由椭圆的定义知,所以所求椭圆的标准方程为课堂小结:分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹a2-c2=b22、求椭圆的标准方程(常用待定系数法)
(1)定位
(2)定量
