一元二次方程复习（一）

课件20张PPT。一元二次方程复习（1）湖南省新邵县酿溪中学王军旗学习目标1 系统了解本章知识结构，掌握本章知识要点。
2 通过训练，能快速准确的解一元二次方程；
3 会利用根的判别式，判断一元二次方程的根的情况。
重点：本章知识要点、一元二次方程的解法。
难点：一元二次方程的解法及根与系数的关系综合运用。
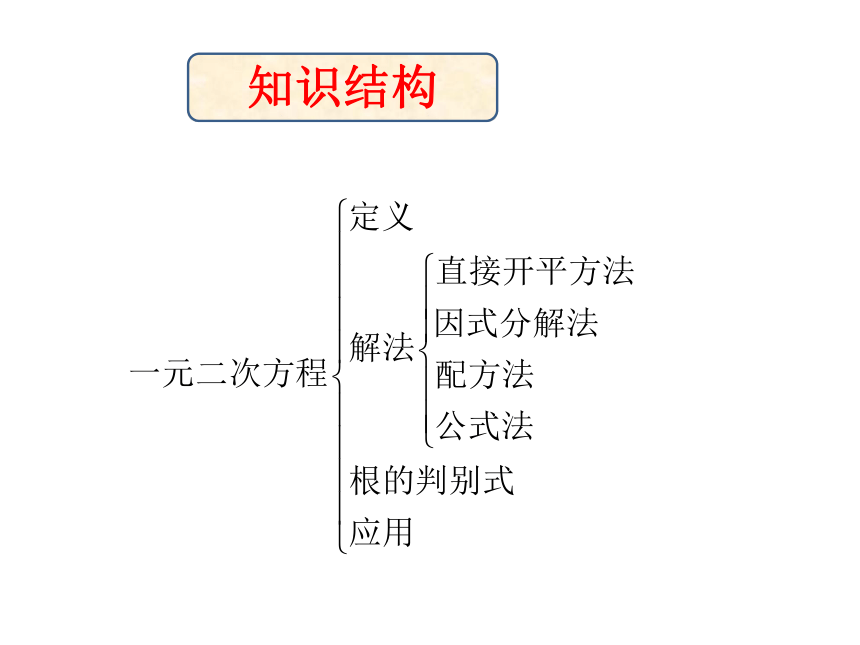
知识结构回顾：本章学习了哪些知识？主题一：一元二次方程的概念【分析】一元二次方程的 三个要素：只含有一个未知数、未知数的最高次数为1、是整式方程2主题二.一元二次方程的解法规律和方法点评：1、形如（x-k）2=h（h ≥ 0）或 x2=h（h ≥ 0）的方程可以用直接开平方法求解
2、千万记住：方程的两边有相同的含有未知数的因式的时候不能两边都除以这个因式，因为这样能把方程的一个根丢失了，要利用因式分解法求解。
3、当方程的左边是二次三项式的时候优先用十字相乘法求解。
当我们不能利用上边的方法求解的时候就就可以用公式法或配方法求解，公式法和配方法是万能的。
【例3】(2010年安徽省芜湖市)关于x的方程(a －5)x2－4x－1＝0有实数根，则a满足（ ）
A．a≥1 B．a＞1且a≠5 C．a≥1且a≠5 D．a≠5
主题三：一元二次方程根的判别式【分析】由于题中“关于x的方程”没有指明已知方程
是一元一次方程还是一元二次方程，因此a-5可以等于0，
也可以不等于0，因此要分情况考虑。解：当a=5时，已知方程是：-4x-1=0,显然这个方程有实数解，x=1
当a≠5时，方程有实数解的条件是：△≥0，即：（-4）2-4（a-5）×(-1) ≥0
16+4(a-5) ≥0,4a-4≥0,a≥1
综上，当a≥1时，已知方程有实数解。故选A.A2010年广东省广州市）已知关于x的一元二次方程
有两个相等的实数根，
求 的值。
强化训练-2解：因为a=6时，方程就是-8x+6=0,显然这个方程有实数根.
当a≠6时，因为方程有实数根，所以△≥0，
即：（-8）2-4（a-6）×6=64-24(a-6) ≥0
8-3（a-6）≥0,-3a+26≥0,a≤ , 则整数a的最大值为8。故选c。
小结：1.一元二次方程的定义要注意隐含条件-----二次项系数不等于零。
2.解一元二次方程要注意选择合适的方法。
3.利用根的判别式解题，要注意二次项系数不为零的条件。作业再见 同学们辛苦了！再见！