2010-2011高一数学集合与函数单元测试
文档属性
| 名称 | 2010-2011高一数学集合与函数单元测试 |
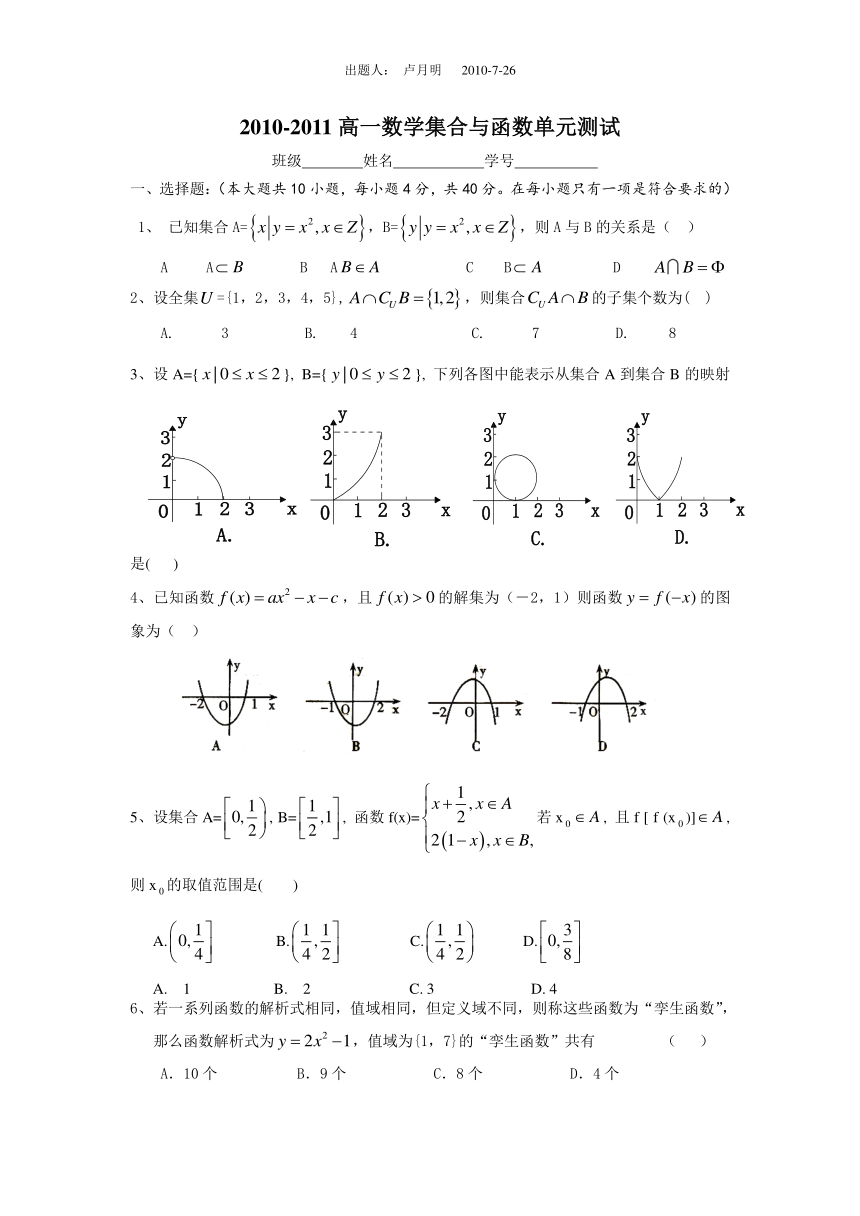
|
|
| 格式 | zip | ||
| 文件大小 | 215.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-06 00:00:00 | ||
图片预览
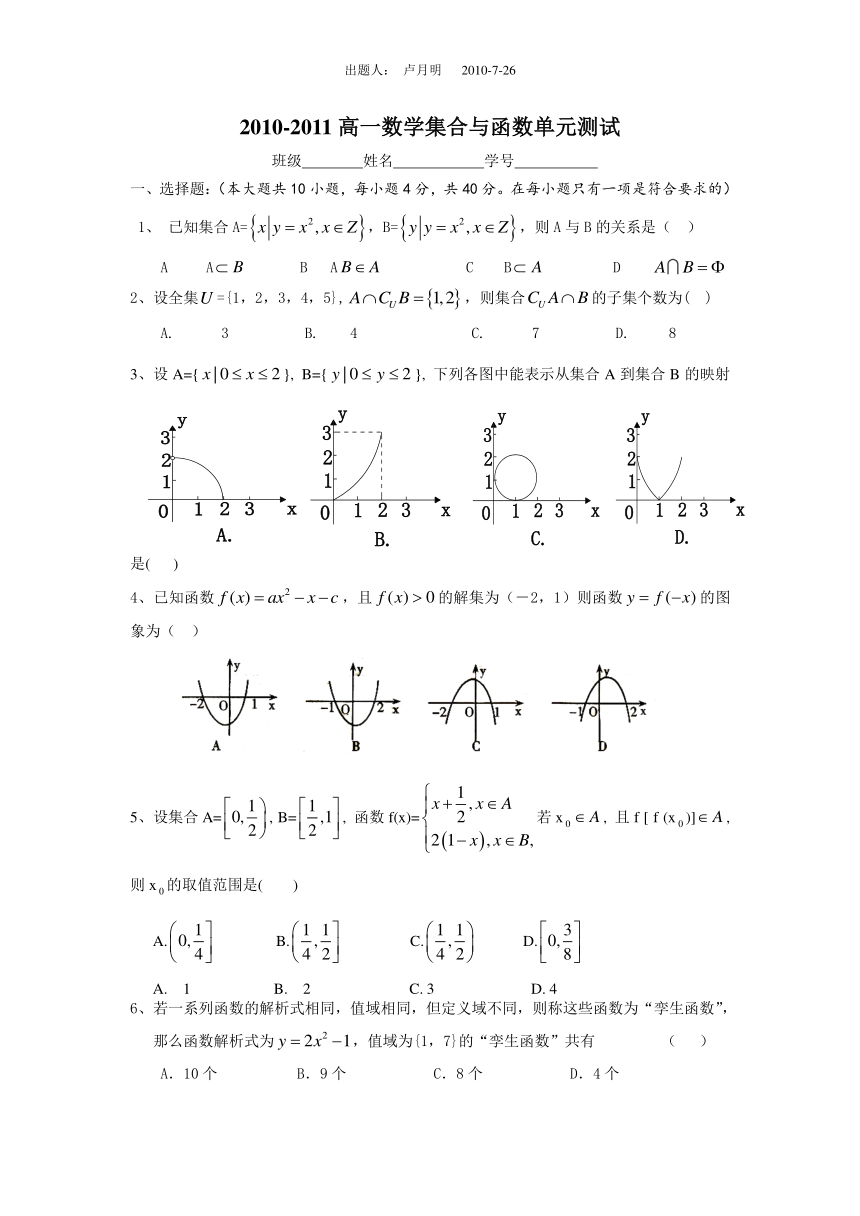



文档简介
出题人: 卢月明 2010-7-26
2010-2011高一数学集合与函数单元测试
班级 姓名 学号
一、选择题:(本大题共10小题,每小题4分,共40分。在每小题只有一项是符合要求的)
1、 已知集合A=,B=,则A与B的关系是( )
A A B A C B D
2、设全集={1,2,3,4,5},,则集合的子集个数为( )
A. 3 B. 4 C. 7 D. 8
3、设A={}, B={}, 下列各图中能表示从集合A到集合B的映射是( )
4、已知函数,且的解集为(-2,1)则函数的图象为( )
5、设集合A=, B=, 函数f(x)=若x, 且f [ f (x)],则x的取值范围是( )
A. B. C. D.
A. 1 B. 2 C. 3 D. 4
6、若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,
那么函数解析式为,值域为{1,7}的“孪生函数”共有 ( )
A.10个 B.9个 C.8个 D.4个
7、函数是 ( )
A.奇函数 B.偶函数 C.非奇非偶函数 D.是奇函数又是偶函数
8、已知 y = f ( x ) 是定义在R 上的偶函数, 且在( 0 , + )上是减函数,如果x1 < 0 , x2 > 0 ,
且| x1 | < | x2 | , 则有( )
A.f (-x1 ) + f (-x2 ) > 0 B. f ( x1 ) + f ( x2 ) < 0
C. f (-x1 ) -f (-x2 ) > 0 D. f ( x1 ) -f ( x2 ) < 0
9、设函数若f(-4)=f(0),f(-2)=-2,则关于x的方程的解的个数为
(A). 1 (B)2 (C)3 (D)4 ( )
10、一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水. 则正确论断的个数是( )
A. 0 B. 1 C. 2 D. 3
二、填空题:本答题共4小题,每小题5分,共20分,把答案填在题中横线上。
11、设f(x)是定义在(0,+)上的减函数,那么f(2)与f(a2+2a+2)的大小关系是_____
12、满足条件{0,1}∪A={0,1}的所有集合A的个数是 个
13、已知,则不等式的解集是
14、 如果函数满足:对任意实数都有,且,则:
______________
15、已知
第一章 《集合与函数概念》单元测试题答卷
选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案
填空题
11、 ; 12 ; 13
14 ; 15
三、解答题:(满分75分,要求写出详细的解题过程)
16、(满分12分)设A={x∈Z| ,,求:
(1); (2)
17、(满分12分)若集合,且,求实数的值。
18、(满分12分)设的解集是(-3,2).
(1)求f(x);
(2)当函数f(x)的定义域是[0,1]时,求函数f(x)的值域.
19、(满分12分)已知奇函数
(1)求实数m的值,并在给出的直角坐标系中画出的图象;
(2)若函数f(x)在区间[-1,|a|-2]上单调递增,试确定a的取值范围.
20、(满分13分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式。
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这
10万元投资,才能是企业获得最大利润,其最大利润约为多少万元。(精确到1万元)。
21、(满分14分)若非零函数对任意实数均有,且当时,;(1)求证: ;(2)求证:为减函数 (3)当时,解不等式
参考答案
一、选择题:CDBDC BBCCB
二、填空题:
11. f(2)> f(a2+2a+2); 12. 4 ; 13. ;
14. 2010 ; 15. 6
三、解答题:
16、解:……………2分
(1)又
……6分
(2)又
得
……………12分
17、解: A={-3, 2}
⑴ 当△<0,即时,B= , B成立 …………………4分
⑵ 当△=0,即时,B={}, B不成立……………8分
⑶ 当△>0,即时,若B成立 则:B={-3, 2}
∴ a= -3x2=-6 ………………………………………12分
18、解:(1)由已知方程f(x)=0的两根为-3和2(a<0)
由韦达定理得
从而…………………………………………6分
(2)=
而对称轴从而上为减函数
所以,当
故所求函数的值域为[12,18]…………………………12分
19、(1)当 x<0时,-x>0,
又f(x)为奇函数,∴,∴ f(x)=x2+2x,∴m=2 ……………4分
y=f(x)的图象如右所示 ……………6分
(2)由(1)知f(x)=,…8分
由图象可知,在[-1,1]上单调递增,要使在[-1,|a|-2]上单调递增,只需 ……………10分
解之得 ……………12分
20、(1)投资为万元,A产品的利润为万元,B产品的利润为万元,
由题设=,=,.
由图知,又
从而=,=, ……………6分
(2)设A产品投入万元,则B产品投入10-万元,设企业的利润为y万元
Y=+=,(),
令
当,,此时=3.75
当A产品投入3.75万元,B产品投入6.25万元时,
企业获得最大利润约为4万元。 ……………12分
21、解:(1)
又若f(x0)=0, 则f(x)=f(x- x0+ x0)=f(x-x0)f(x0)=0与已经矛盾,
故 f(x)> 0 …………………………4分
(2)设则 又 ∵为非零函数
=,
为减函数 …………………………9分
(3)由
原不等式转化为,结合(2)得:
故不等式的解集为; …………………………14分
2010-2011高一数学集合与函数单元测试
班级 姓名 学号
一、选择题:(本大题共10小题,每小题4分,共40分。在每小题只有一项是符合要求的)
1、 已知集合A=,B=,则A与B的关系是( )
A A B A C B D
2、设全集={1,2,3,4,5},,则集合的子集个数为( )
A. 3 B. 4 C. 7 D. 8
3、设A={}, B={}, 下列各图中能表示从集合A到集合B的映射是( )
4、已知函数,且的解集为(-2,1)则函数的图象为( )
5、设集合A=, B=, 函数f(x)=若x, 且f [ f (x)],则x的取值范围是( )
A. B. C. D.
A. 1 B. 2 C. 3 D. 4
6、若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,
那么函数解析式为,值域为{1,7}的“孪生函数”共有 ( )
A.10个 B.9个 C.8个 D.4个
7、函数是 ( )
A.奇函数 B.偶函数 C.非奇非偶函数 D.是奇函数又是偶函数
8、已知 y = f ( x ) 是定义在R 上的偶函数, 且在( 0 , + )上是减函数,如果x1 < 0 , x2 > 0 ,
且| x1 | < | x2 | , 则有( )
A.f (-x1 ) + f (-x2 ) > 0 B. f ( x1 ) + f ( x2 ) < 0
C. f (-x1 ) -f (-x2 ) > 0 D. f ( x1 ) -f ( x2 ) < 0
9、设函数若f(-4)=f(0),f(-2)=-2,则关于x的方程的解的个数为
(A). 1 (B)2 (C)3 (D)4 ( )
10、一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水. 则正确论断的个数是( )
A. 0 B. 1 C. 2 D. 3
二、填空题:本答题共4小题,每小题5分,共20分,把答案填在题中横线上。
11、设f(x)是定义在(0,+)上的减函数,那么f(2)与f(a2+2a+2)的大小关系是_____
12、满足条件{0,1}∪A={0,1}的所有集合A的个数是 个
13、已知,则不等式的解集是
14、 如果函数满足:对任意实数都有,且,则:
______________
15、已知
第一章 《集合与函数概念》单元测试题答卷
选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案
填空题
11、 ; 12 ; 13
14 ; 15
三、解答题:(满分75分,要求写出详细的解题过程)
16、(满分12分)设A={x∈Z| ,,求:
(1); (2)
17、(满分12分)若集合,且,求实数的值。
18、(满分12分)设的解集是(-3,2).
(1)求f(x);
(2)当函数f(x)的定义域是[0,1]时,求函数f(x)的值域.
19、(满分12分)已知奇函数
(1)求实数m的值,并在给出的直角坐标系中画出的图象;
(2)若函数f(x)在区间[-1,|a|-2]上单调递增,试确定a的取值范围.
20、(满分13分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式。
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这
10万元投资,才能是企业获得最大利润,其最大利润约为多少万元。(精确到1万元)。
21、(满分14分)若非零函数对任意实数均有,且当时,;(1)求证: ;(2)求证:为减函数 (3)当时,解不等式
参考答案
一、选择题:CDBDC BBCCB
二、填空题:
11. f(2)> f(a2+2a+2); 12. 4 ; 13. ;
14. 2010 ; 15. 6
三、解答题:
16、解:……………2分
(1)又
……6分
(2)又
得
……………12分
17、解: A={-3, 2}
⑴ 当△<0,即时,B= , B成立 …………………4分
⑵ 当△=0,即时,B={}, B不成立……………8分
⑶ 当△>0,即时,若B成立 则:B={-3, 2}
∴ a= -3x2=-6 ………………………………………12分
18、解:(1)由已知方程f(x)=0的两根为-3和2(a<0)
由韦达定理得
从而…………………………………………6分
(2)=
而对称轴从而上为减函数
所以,当
故所求函数的值域为[12,18]…………………………12分
19、(1)当 x<0时,-x>0,
又f(x)为奇函数,∴,∴ f(x)=x2+2x,∴m=2 ……………4分
y=f(x)的图象如右所示 ……………6分
(2)由(1)知f(x)=,…8分
由图象可知,在[-1,1]上单调递增,要使在[-1,|a|-2]上单调递增,只需 ……………10分
解之得 ……………12分
20、(1)投资为万元,A产品的利润为万元,B产品的利润为万元,
由题设=,=,.
由图知,又
从而=,=, ……………6分
(2)设A产品投入万元,则B产品投入10-万元,设企业的利润为y万元
Y=+=,(),
令
当,,此时=3.75
当A产品投入3.75万元,B产品投入6.25万元时,
企业获得最大利润约为4万元。 ……………12分
21、解:(1)
又若f(x0)=0, 则f(x)=f(x- x0+ x0)=f(x-x0)f(x0)=0与已经矛盾,
故 f(x)> 0 …………………………4分
(2)设则 又 ∵为非零函数
=,
为减函数 …………………………9分
(3)由
原不等式转化为,结合(2)得:
故不等式的解集为; …………………………14分
