九年级上册第19.1~19.3水平测试题
文档属性
| 名称 | 九年级上册第19.1~19.3水平测试题 |

|
|
| 格式 | rar | ||
| 文件大小 | 50.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-06 00:00:00 | ||
图片预览


文档简介
九年级上册第19.1~19.3水平测试题
跟踪反馈 挑战自我(100分)
一、选择题
1、下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d= B.a=4,b=6,c=5,d=10
C.a=2,b=,c=2,d= D.a=2,b=3,c=4,d=1
2、已知,则下列式子中正确的是( )
A.a∶b=c2∶d2 B.a∶d=c∶b
C.a∶b=(a+c)∶(b+d) D.a∶b=(a-d)∶(b-d)
3、已知点M将线段AB黄金分割(AM>BM),则下列各式中不正确的是( )
A.AM∶BM=AB∶AM B.AM=AB
C.BM=AB D.AM≈0.618AB
4、下列结论不正确的是( )
A.所有的矩形都相似 B.所有的正方形都相似
C.所有的等腰直角三角形都相似 D.所有的正八边形都相似
5、如果一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是( )
A.2∶1 B.4∶1
C.∶1 D.1∶
6、梯形ABCD中,AD∥BC,AD=a,BC=b,EF∥AD交AB、CD于E、F,且梯形AEFD与梯形EBCF相似,则EF等于( )
A. B.
C. D.不能确定
7、把ab=cd写成比例式,不正确的写法是( )
A. B.
C. D.
8、有以下命题:
①如果线段d是线段a,b,c的第四比例项,则有
②如果点C是线段AB的中点,那么AC是AB、BC的比例中项
③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB与BC的比例中项
④如果点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC=-1
其中正确的判断有( )
A.1个 B.2个
C.3个 D.4个
二、填空题
1、如果,那么=________.
2、黄金矩形的宽与长的比大约为________(精确到0.001)
3、两个相似多边形的对应边的比是,则这两个多边形的相似比是________.
4、两个相似多边形的相似比是,则这两个多边形的对应对角线的比是________.
5、在菱形ABCD和菱形A′B′C′D′中,∠A=∠A′=60°,若AB∶A′B′=1∶,则BD∶A′C′=________.
6、以下五个命题:①所有的正方形都相似 ②所有的矩形都相似 ③所有的三角形都相似 ④所有的等腰直角三角形都相似 ⑤所有的正五边形都相似.
其中正确的命题有_______
7、相同时刻的物高与影长成比例,如果有一根电线杆在地面上的影长是50米,同时高为1.5米的标竿的影长为2.5米,那么这根电线杆的高为________米.
8、已知三个数1,2,,请你再写一个数,使这四个数能成比例,那么这个数是________(填写一个即可)
三、解答题
1、已知四条线段a、b、c、d的长度,试判断它们是否成比例?
(1)a=16 cm b=8 cm c=5 cm d=10 cm
(2)a=8 cm b=5 cm c=6 cm d=10 cm
2、已知实数a,b,c满足,求的值.
3、如果一个矩形ABCD(AB<BC)中,≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图1),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性.
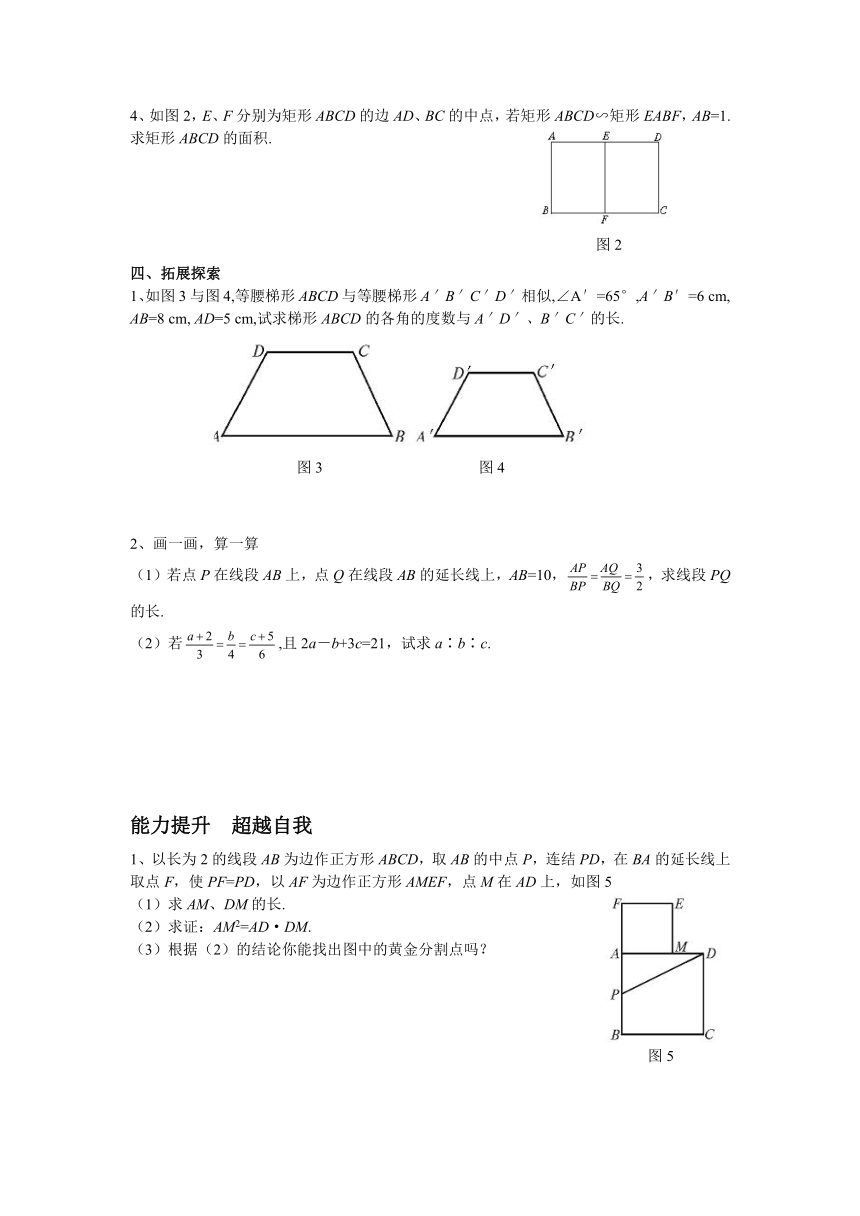
4、如图2,E、F分别为矩形ABCD的边AD、BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD的面积.
四、拓展探索
1、如图3与图4,等腰梯形ABCD与等腰梯形A′B′C′D′相似,∠A′=65°,A′B′=6 cm, AB=8 cm, AD=5 cm,试求梯形ABCD的各角的度数与A′D′、B′C′的长.
2、画一画,算一算
(1)若点P在线段AB上,点Q在线段AB的延长线上,AB=10,,求线段PQ的长.
(2)若,且2a-b+3c=21,试求a∶b∶c.
能力提升 超越自我
1、以长为2的线段AB为边作正方形ABCD,取AB的中点P,连结PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,如图5
(1)求AM、DM的长.
(2)求证:AM2=AD·DM.
(3)根据(2)的结论你能找出图中的黄金分割点吗?
2、如图6,已知A(0,-2),B(-2,1),C(3,2)
(1)求线段AB、BC、AC的长.
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求A′B′、B′C′、A′C′的长.
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
参考答案:
跟踪反馈 挑战自我
一、1、C;2、C;3、C;4、A ;5、C;6、A;7、B;8、C;
二、1、;2、0.618;3、;4、;5、1∶3;6、①④⑤;7、30;8、2或或(填写一个即可)
三、1、(1)=2 =2则 所以a、b、d、c成比例
(2)由已知得:ab≠cd,ac≠bd,ad≠bc,所以a、b、c、d四条线段不成比例
2、解:设=k
则b+c=ak,c+a=bk,a+b=ck
∴2(a+b+c)=k(a+b+c)
当a+b+c≠0时,∴k=2,∴=2
当a+b+c=0时,b=-(b+c), =-1
3、矩形ABFE是黄金矩形 由于,设AB=(-1)k,BC=2k,所以FC=CD=AB,BF=BC-FC=BC-AB=2k-(-1)k=(3-)k,所以,所以矩形ABFE是黄金矩形
4、由矩形ABCD∽矩形EABF可得,设AE=x,则BC=2x,又AB=1,所以,S矩形ABCD=2x·1=
四、1、(1)∵等腰梯形ABCD与A′B′C′D′相似,∠A′=65°,∴∠A=65°,
∠B=65°,∠D=∠C=180°-65°=115°,又,∴,∴A′D′=cm,
∴B′C′=A′D′=cm
2、(1)设AP=3x,BP=2x
∵AB=10
∴AB=AP+BP=3x+2x=5x,即5x=10,
∴x=2 ∴AP=6,BP=4
∵,∴可设BQ=y,则AQ=AB+BQ=10+y
∴,解得:y=20,
∴PQ=PB+BQ=4+20=24
(2)令=m,则a+2=3m,b=4m,c+5=6m
∴a=3m-2,b=4m,c=6m-5
∵2a-b+3c=21
∴2(3m-2)-4m+3(6m-5)=21,即20m=40
解得m=2
∴a=3m-2=4,b=4m=8,c=6m-5=7
∴a∶b∶c=4∶8∶7
能力提升 超越自我
1、解:如图(见原题图)
(1)∵正方形ABCD的边长为2,P是AB中点
∴AB=AD=2,AP=1
在Rt△APD中,PD=
∵PF=PD,
∴AF=PF-AP=-1
∵AMEF是正方形,
∴AM=AF=-1
DM=AD-AM=2-(-1)=3-
(2)由(1)得AM2=(-1)2=6-2
AD·DM=2(3-)=6-2
∴AM2=AD·DM
(3)图中点M是线段AD的黄金分割点.
2、解:如图(见原题图)A(0,-2),B(-2,1),C(3,2)
(1)由勾股定理得:
AB=
BC=
AC==5
(2)由已知得A′(0,-4),B′(-4,2),C′(6,4)
由勾股定理得:
A′B′=
B′C′=
A′C′==10
(3)∵
∴这六条线段成比例
(4)△ABC与△A′B′C′的形状相同.
图1
图2
图4
图3
图5
图6
跟踪反馈 挑战自我(100分)
一、选择题
1、下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d= B.a=4,b=6,c=5,d=10
C.a=2,b=,c=2,d= D.a=2,b=3,c=4,d=1
2、已知,则下列式子中正确的是( )
A.a∶b=c2∶d2 B.a∶d=c∶b
C.a∶b=(a+c)∶(b+d) D.a∶b=(a-d)∶(b-d)
3、已知点M将线段AB黄金分割(AM>BM),则下列各式中不正确的是( )
A.AM∶BM=AB∶AM B.AM=AB
C.BM=AB D.AM≈0.618AB
4、下列结论不正确的是( )
A.所有的矩形都相似 B.所有的正方形都相似
C.所有的等腰直角三角形都相似 D.所有的正八边形都相似
5、如果一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是( )
A.2∶1 B.4∶1
C.∶1 D.1∶
6、梯形ABCD中,AD∥BC,AD=a,BC=b,EF∥AD交AB、CD于E、F,且梯形AEFD与梯形EBCF相似,则EF等于( )
A. B.
C. D.不能确定
7、把ab=cd写成比例式,不正确的写法是( )
A. B.
C. D.
8、有以下命题:
①如果线段d是线段a,b,c的第四比例项,则有
②如果点C是线段AB的中点,那么AC是AB、BC的比例中项
③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB与BC的比例中项
④如果点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC=-1
其中正确的判断有( )
A.1个 B.2个
C.3个 D.4个
二、填空题
1、如果,那么=________.
2、黄金矩形的宽与长的比大约为________(精确到0.001)
3、两个相似多边形的对应边的比是,则这两个多边形的相似比是________.
4、两个相似多边形的相似比是,则这两个多边形的对应对角线的比是________.
5、在菱形ABCD和菱形A′B′C′D′中,∠A=∠A′=60°,若AB∶A′B′=1∶,则BD∶A′C′=________.
6、以下五个命题:①所有的正方形都相似 ②所有的矩形都相似 ③所有的三角形都相似 ④所有的等腰直角三角形都相似 ⑤所有的正五边形都相似.
其中正确的命题有_______
7、相同时刻的物高与影长成比例,如果有一根电线杆在地面上的影长是50米,同时高为1.5米的标竿的影长为2.5米,那么这根电线杆的高为________米.
8、已知三个数1,2,,请你再写一个数,使这四个数能成比例,那么这个数是________(填写一个即可)
三、解答题
1、已知四条线段a、b、c、d的长度,试判断它们是否成比例?
(1)a=16 cm b=8 cm c=5 cm d=10 cm
(2)a=8 cm b=5 cm c=6 cm d=10 cm
2、已知实数a,b,c满足,求的值.
3、如果一个矩形ABCD(AB<BC)中,≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图1),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性.
4、如图2,E、F分别为矩形ABCD的边AD、BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD的面积.
四、拓展探索
1、如图3与图4,等腰梯形ABCD与等腰梯形A′B′C′D′相似,∠A′=65°,A′B′=6 cm, AB=8 cm, AD=5 cm,试求梯形ABCD的各角的度数与A′D′、B′C′的长.
2、画一画,算一算
(1)若点P在线段AB上,点Q在线段AB的延长线上,AB=10,,求线段PQ的长.
(2)若,且2a-b+3c=21,试求a∶b∶c.
能力提升 超越自我
1、以长为2的线段AB为边作正方形ABCD,取AB的中点P,连结PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,如图5
(1)求AM、DM的长.
(2)求证:AM2=AD·DM.
(3)根据(2)的结论你能找出图中的黄金分割点吗?
2、如图6,已知A(0,-2),B(-2,1),C(3,2)
(1)求线段AB、BC、AC的长.
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求A′B′、B′C′、A′C′的长.
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
参考答案:
跟踪反馈 挑战自我
一、1、C;2、C;3、C;4、A ;5、C;6、A;7、B;8、C;
二、1、;2、0.618;3、;4、;5、1∶3;6、①④⑤;7、30;8、2或或(填写一个即可)
三、1、(1)=2 =2则 所以a、b、d、c成比例
(2)由已知得:ab≠cd,ac≠bd,ad≠bc,所以a、b、c、d四条线段不成比例
2、解:设=k
则b+c=ak,c+a=bk,a+b=ck
∴2(a+b+c)=k(a+b+c)
当a+b+c≠0时,∴k=2,∴=2
当a+b+c=0时,b=-(b+c), =-1
3、矩形ABFE是黄金矩形 由于,设AB=(-1)k,BC=2k,所以FC=CD=AB,BF=BC-FC=BC-AB=2k-(-1)k=(3-)k,所以,所以矩形ABFE是黄金矩形
4、由矩形ABCD∽矩形EABF可得,设AE=x,则BC=2x,又AB=1,所以,S矩形ABCD=2x·1=
四、1、(1)∵等腰梯形ABCD与A′B′C′D′相似,∠A′=65°,∴∠A=65°,
∠B=65°,∠D=∠C=180°-65°=115°,又,∴,∴A′D′=cm,
∴B′C′=A′D′=cm
2、(1)设AP=3x,BP=2x
∵AB=10
∴AB=AP+BP=3x+2x=5x,即5x=10,
∴x=2 ∴AP=6,BP=4
∵,∴可设BQ=y,则AQ=AB+BQ=10+y
∴,解得:y=20,
∴PQ=PB+BQ=4+20=24
(2)令=m,则a+2=3m,b=4m,c+5=6m
∴a=3m-2,b=4m,c=6m-5
∵2a-b+3c=21
∴2(3m-2)-4m+3(6m-5)=21,即20m=40
解得m=2
∴a=3m-2=4,b=4m=8,c=6m-5=7
∴a∶b∶c=4∶8∶7
能力提升 超越自我
1、解:如图(见原题图)
(1)∵正方形ABCD的边长为2,P是AB中点
∴AB=AD=2,AP=1
在Rt△APD中,PD=
∵PF=PD,
∴AF=PF-AP=-1
∵AMEF是正方形,
∴AM=AF=-1
DM=AD-AM=2-(-1)=3-
(2)由(1)得AM2=(-1)2=6-2
AD·DM=2(3-)=6-2
∴AM2=AD·DM
(3)图中点M是线段AD的黄金分割点.
2、解:如图(见原题图)A(0,-2),B(-2,1),C(3,2)
(1)由勾股定理得:
AB=
BC=
AC==5
(2)由已知得A′(0,-4),B′(-4,2),C′(6,4)
由勾股定理得:
A′B′=
B′C′=
A′C′==10
(3)∵
∴这六条线段成比例
(4)△ABC与△A′B′C′的形状相同.
图1
图2
图4
图3
图5
图6
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
