(新人教a版必修2)数学:1.3空间几何体的表面积与体积(课件)
文档属性
| 名称 | (新人教a版必修2)数学:1.3空间几何体的表面积与体积(课件) |  | |
| 格式 | rar | ||
| 文件大小 | 150.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-08 09:51:00 | ||
图片预览



文档简介
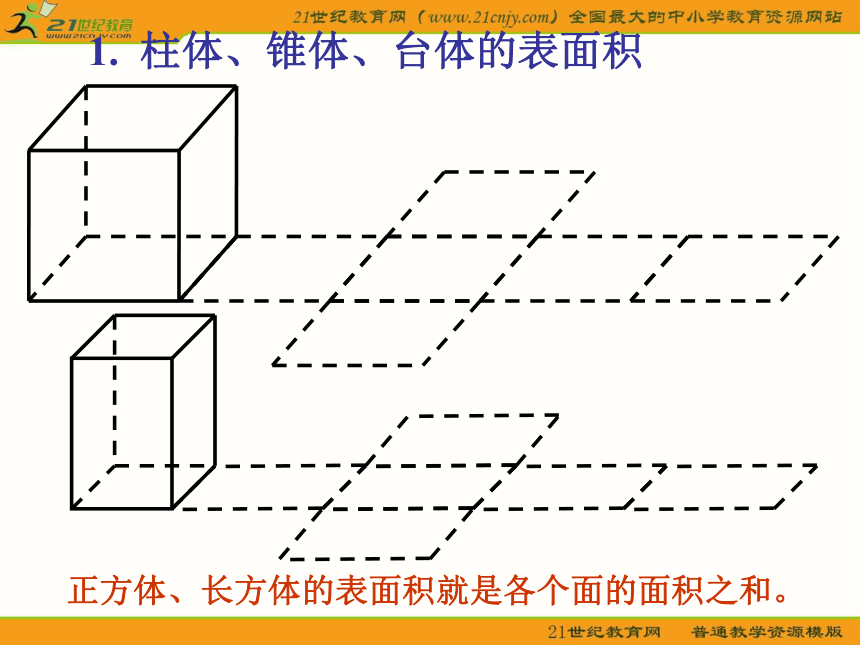
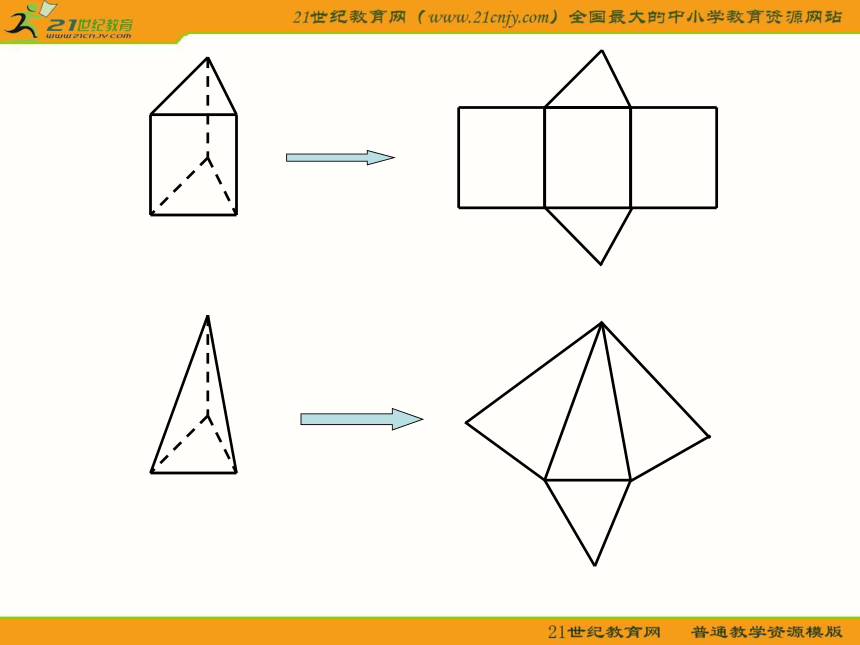
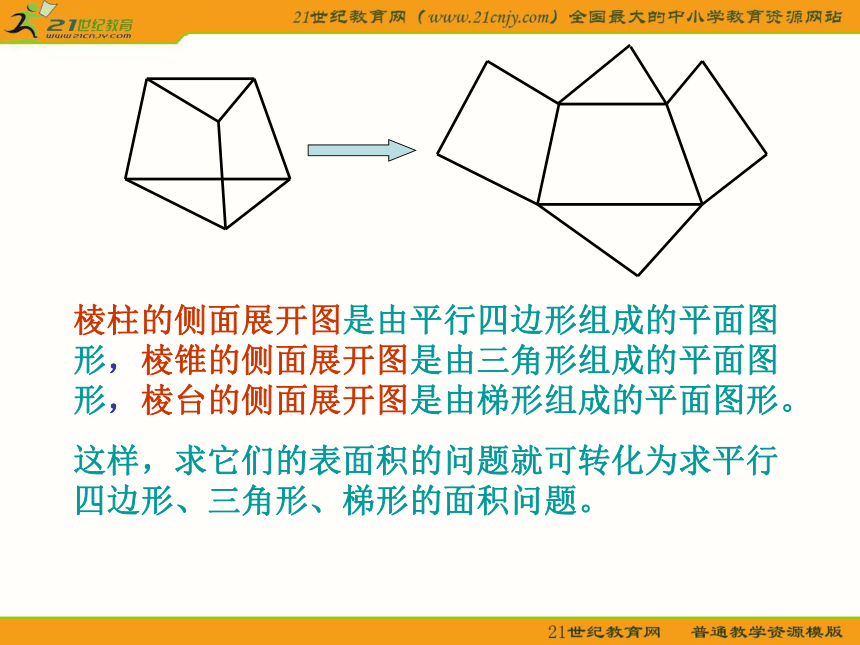
课件26张PPT。1、3 空间几何体的表面积与体积1. 柱体、锥体、台体的表面积正方体、长方体的表面积就是各个面的面积之和。探究 棱柱、棱锥、棱台也是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?棱柱的侧面展开图是由平行四边形组成的平面图形,棱锥的侧面展开图是由三角形组成的平面图形,棱台的侧面展开图是由梯形组成的平面图形。
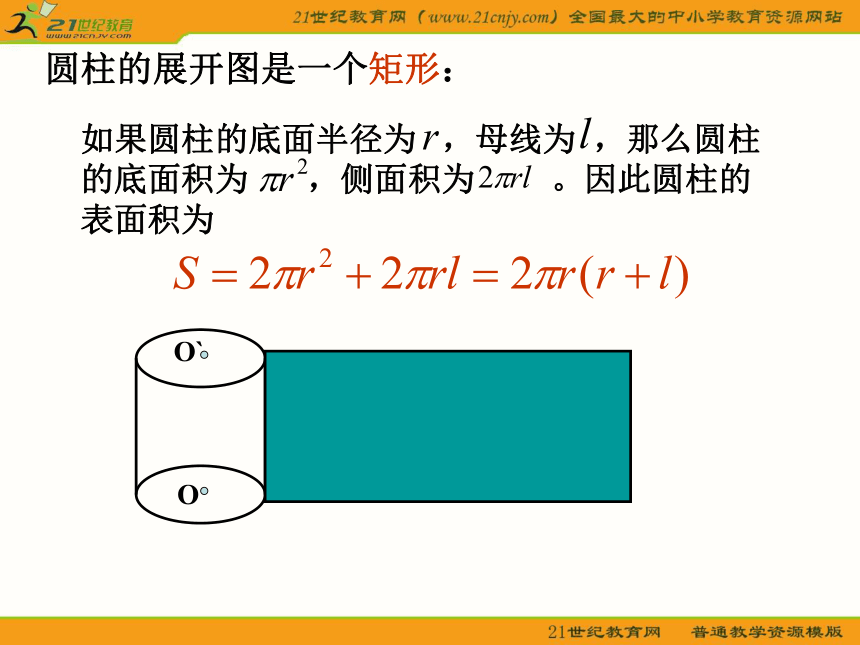
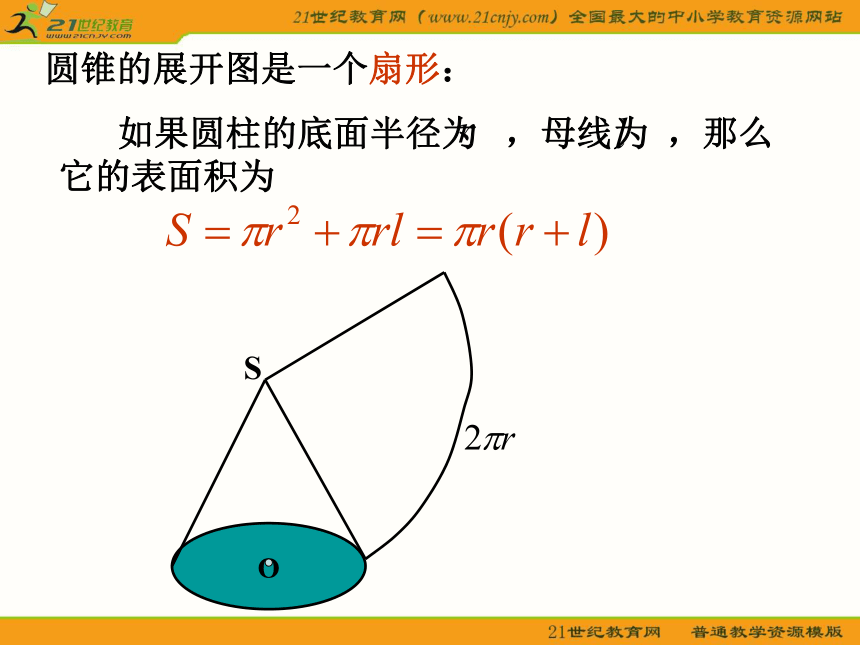
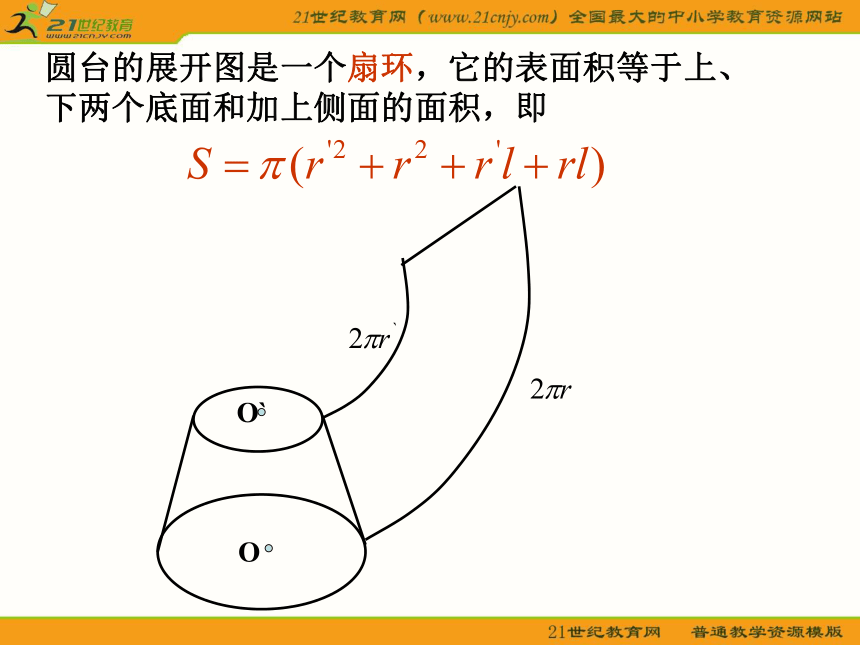
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。D圆柱的展开图是一个矩形:如果圆柱的底面半径为 ,母线为 ,那么圆柱的底面积为 ,侧面积为 。因此圆柱的表面积为圆锥的展开图是一个扇形: 如果圆柱的底面半径为 ,母线为 ,那么它的表面积为圆台的展开图是一个扇环,它的表面积等于上、下两个底面和加上侧面的面积,即柱体、锥体、台体的体积正方体、长方体,以及圆柱的体积公式可以统一为:V = Sh(S为底面面积,h为高)一般棱柱的体积公式也是V = Sh,其中S为底面面积,h为高。棱锥的体积公式也是 ,其中S为底面面积,h为高。
即它是同底同高的圆柱的体积的 。探究探究棱锥与同底等高的棱柱体积之间的关系?圆台(棱台)的体积公式:其是S‘,S分别为上底面面积,h为圆台(棱台)高。练习1 . 若一个圆柱的侧面展开图是一个正方形,
则这个圆柱的全面积与侧面积的比是( )A . B . C . D . A2 . 已知圆锥的全面积是底面积的3倍,那么这个
圆锥的侧面积展开图----扇形的圆心角为____
______度180小结本节课主要介绍了求几何体的表面积的方法:
将空间图形问题转化为平面图形问题,
利用平面图形求面积的方法求立体图
形的表面积球面:半圆以它的直径为旋转轴,旋转所成的曲面。球(即球体):球面所围成的几何体。它包括球面和球面所包围的空间。半径是R的球的体积:推导方法: 分割求近似和化为准确和复习回顾第一步:分割O球面被分割成n个网格,
表面积分别为:则球的表面积:则球的体积为:设“小锥体”的体积为:2、球的表面积O第二步:求近似和O由第一步得:第三步:转化为球的表面积 如果网格分的越细,则:① 由①② 得:(1)若球的表面积变为原来的2倍,则半径变为原来的—倍。
(2)若球半径变为原来的2倍,则表面积变为原来的—倍。
(3)若两球表面积之比为1:2,则其体积之比是———。
(4)若两球体积之比是1:2,则其表面积之比是———。练习一:例1、如图表示一个用鲜花作成的花柱,它的下面是一个直径为1m、高为3m的圆柱形物体,上面是一个半球形体。如果每平方米大约需要鲜花150朵,那么装饰这个花柱大约需要多少朵鲜花(π取3.1)?例2.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O和这个正方体的六个面都相切,则有S=——。
变题2.如果球O和这个正方体的各条棱都相切,则有S=——。关键:找正方体的棱长a与球半径R之间的关系试根据以上数据,判断钢球是实心的还是空心的。如果是空心的,请你计算出它的内径(π取3.14,结果精确到1cm)。例3、有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.作轴截面1.球的直径伸长为原来的2倍,体积变为原来的几倍?
2.一个正方体的顶点都在球面上,它的棱长是4cm,求这个球的体积. 课堂练习8倍小结1.一种方法: “分割,求和,取极限”的数学方法.2.一个观点:在一定条件下,化曲为直的辨证观点.3.二个公式
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。D圆柱的展开图是一个矩形:如果圆柱的底面半径为 ,母线为 ,那么圆柱的底面积为 ,侧面积为 。因此圆柱的表面积为圆锥的展开图是一个扇形: 如果圆柱的底面半径为 ,母线为 ,那么它的表面积为圆台的展开图是一个扇环,它的表面积等于上、下两个底面和加上侧面的面积,即柱体、锥体、台体的体积正方体、长方体,以及圆柱的体积公式可以统一为:V = Sh(S为底面面积,h为高)一般棱柱的体积公式也是V = Sh,其中S为底面面积,h为高。棱锥的体积公式也是 ,其中S为底面面积,h为高。
即它是同底同高的圆柱的体积的 。探究探究棱锥与同底等高的棱柱体积之间的关系?圆台(棱台)的体积公式:其是S‘,S分别为上底面面积,h为圆台(棱台)高。练习1 . 若一个圆柱的侧面展开图是一个正方形,
则这个圆柱的全面积与侧面积的比是( )A . B . C . D . A2 . 已知圆锥的全面积是底面积的3倍,那么这个
圆锥的侧面积展开图----扇形的圆心角为____
______度180小结本节课主要介绍了求几何体的表面积的方法:
将空间图形问题转化为平面图形问题,
利用平面图形求面积的方法求立体图
形的表面积球面:半圆以它的直径为旋转轴,旋转所成的曲面。球(即球体):球面所围成的几何体。它包括球面和球面所包围的空间。半径是R的球的体积:推导方法: 分割求近似和化为准确和复习回顾第一步:分割O球面被分割成n个网格,
表面积分别为:则球的表面积:则球的体积为:设“小锥体”的体积为:2、球的表面积O第二步:求近似和O由第一步得:第三步:转化为球的表面积 如果网格分的越细,则:① 由①② 得:(1)若球的表面积变为原来的2倍,则半径变为原来的—倍。
(2)若球半径变为原来的2倍,则表面积变为原来的—倍。
(3)若两球表面积之比为1:2,则其体积之比是———。
(4)若两球体积之比是1:2,则其表面积之比是———。练习一:例1、如图表示一个用鲜花作成的花柱,它的下面是一个直径为1m、高为3m的圆柱形物体,上面是一个半球形体。如果每平方米大约需要鲜花150朵,那么装饰这个花柱大约需要多少朵鲜花(π取3.1)?例2.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O和这个正方体的六个面都相切,则有S=——。
变题2.如果球O和这个正方体的各条棱都相切,则有S=——。关键:找正方体的棱长a与球半径R之间的关系试根据以上数据,判断钢球是实心的还是空心的。如果是空心的,请你计算出它的内径(π取3.14,结果精确到1cm)。例3、有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.作轴截面1.球的直径伸长为原来的2倍,体积变为原来的几倍?
2.一个正方体的顶点都在球面上,它的棱长是4cm,求这个球的体积. 课堂练习8倍小结1.一种方法: “分割,求和,取极限”的数学方法.2.一个观点:在一定条件下,化曲为直的辨证观点.3.二个公式
