(新人教a版必修2)数学:2.1《空间点、直线与平面的位置关系》课件
文档属性
| 名称 | (新人教a版必修2)数学:2.1《空间点、直线与平面的位置关系》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-08 09:51:00 | ||
图片预览





文档简介
课件23张PPT。2.1《空间点、
直线与平面的位置关系》1、掌握平面的表示法及水平放置的直观图;
2、会用符号表示出点与直线,点与平面,直线和平面以及平面与平面相交的位置关系;
3、掌握平面的基本性质(三个公理)及作用;
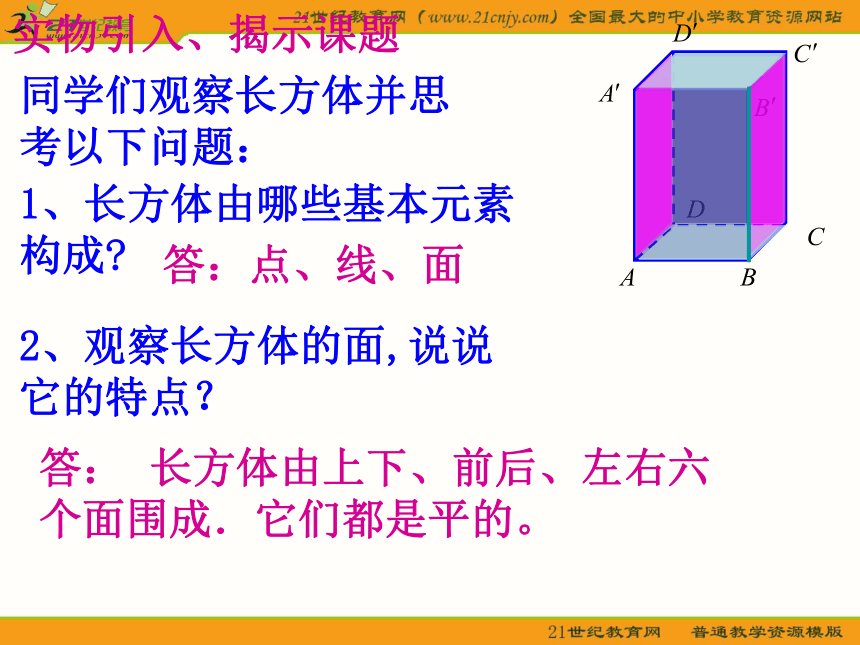
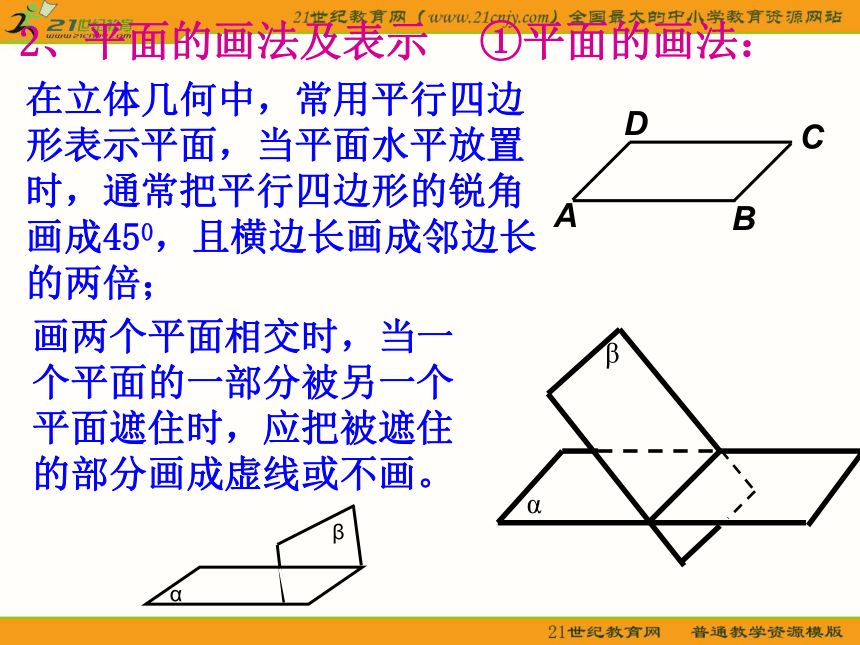
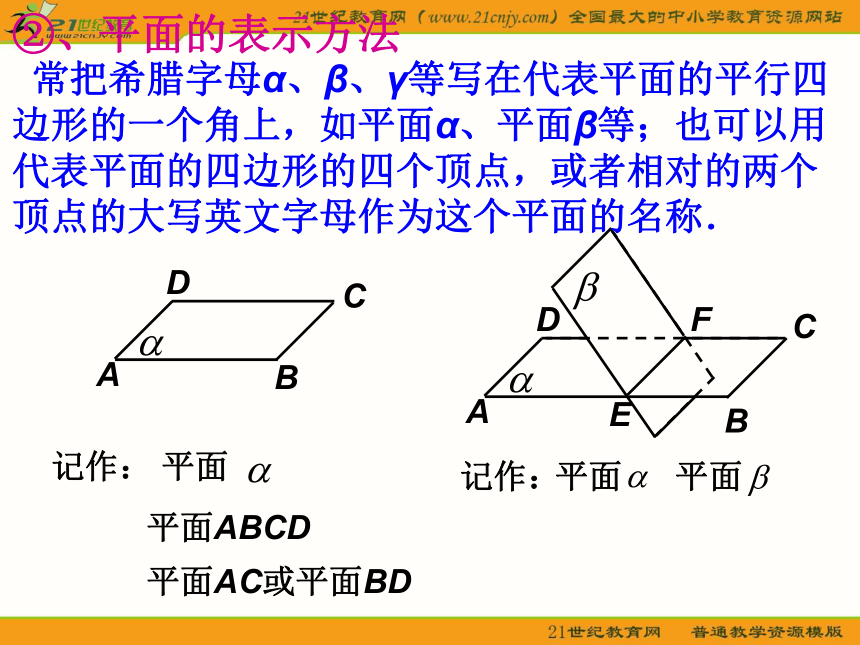
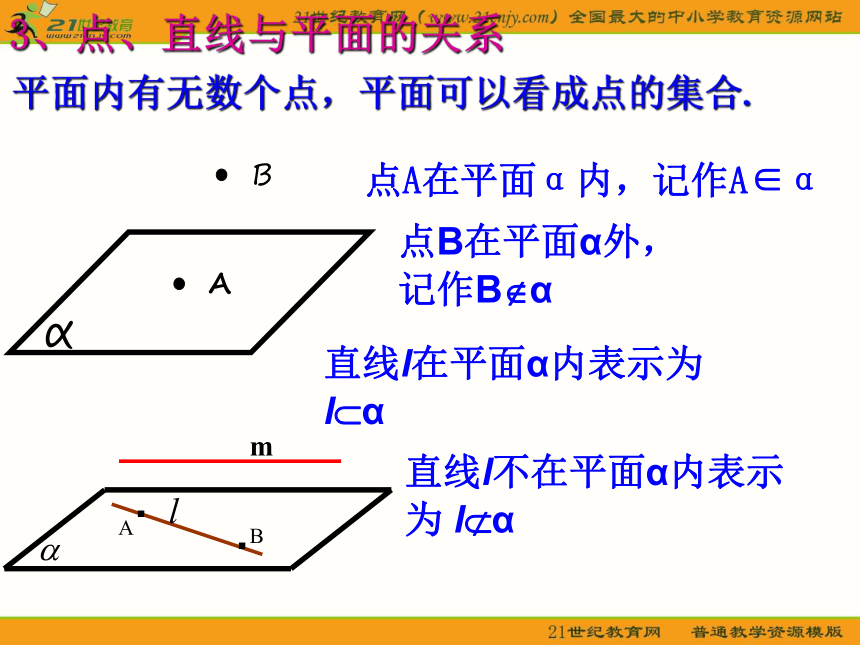
4、培养学生的空间想象能力。教学目标平面实物引入、揭示课题同学们观察长方体并思考以下问题:1、长方体由哪些基本元素构成?2、观察长方体的面,说说它的特点??答:点、线、面答: 长方体由上下、前后、左右六个面围成.它们都是平的。长方体的面给我们以平面的印象;生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的印象。实物引入、揭示课题1、平面的含义以上实物都给我们以平面的印象,几何里所说的平面,就是从这样的一些物体中抽象出来的。平面是没有厚薄的,可以无限延伸,这是平面最基本的属性。常见的桌面,黑板面,平静的水面等都是平面的局部形象;一个平面把空间分成两部分,一条直线把平面分成两部分2、平面的画法及表示①平面的画法:在立体几何中,常用平行四边形表示平面,当平面水平放置时,通常把平行四边形的锐角画成450,且横边长画成邻边长的两倍;画两个平面相交时,当一个平面的一部分被另一个平面遮住时,应把被遮住的部分画成虚线或不画。②、平面的表示方法平面 常把希腊字母α、β、γ等写在代表平面的平行四边形的一个角上,如平面α、平面β等;也可以用代表平面的四边形的四个顶点,或者相对的两个顶点的大写英文字母作为这个平面的名称.3、点、直线与平面的关系平面内有无数个点,平面可以看成点的集合.点A在平面α内,记作A∈α点B在平面α外,
记作B?α 直线l在平面α内表示为
l?α直线l不在平面α内表示为 l?α练习思考4、平面的基本性质如果直线 l 与平面α有一个公共点,直线 l 是否在平面α内?如果直线 l 与
平面α有两个公共点呢?实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.图形语言符号语言B··A·..公理1:如果一条直线上的两点在一个平面内,
那么这条直线在此平面内.用途:可以用来判断直线是否在平面内.4、平面的基本性质 在生产、生活中,人们经过长期观察与实践,总结出关于平面的一些基本性质,我们把它作为公理.这些公理是进一步推理的基础.生活中经常看到用三角架支撑照相机.或测量用的平板仪等等……4、平面的基本性质公理2 过不在一条直线上的三点,有且只有一个平面.存在性唯一性作用:
确定平面的主要依据. 不再一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.4、平面的基本性质补充3个推论:4、平面的基本性质推论1:经过一条直线与直线外一点,有且只有一个平面。
推论2:经过两条平行直线,有且只有一个平面。
推论3:经过两条相交直线,有且只有一个平面。 把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B ?为什么?思考4、平面的基本性质 观察长方体,你能发现长方体的两个相交平面有没有公共直线吗?观察 这条公共直线B’C’叫做这两个平面A’B’C’D’和平面BB’C’C的交线. 另一方面,相邻两个平面有一个公共点,如平面A’B’C’D’和平面BB’C’C有一个公共点B’,经过点B有且只有一条过该点的公共直线B’C’.4、平面的基本性质公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.②判断点在直线上.4、平面的基本性质符号表示为:图形表示为:例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.(1)(2)解:在(1)中,在(2)中,例题示范课堂练习:课本P44?练习1、2、3、4补练:①有三个公共点的两个平面重合
②梯形的四个顶点在同一个平面内
③三条互相平行的直线必共面
④ 四条线段顺次首尾连接,构成平面图形2、下列命题正确的是 ( )A、两条直线可以确定一个平面
B、一条直线和一个点可以确定一个平面
C、空间不同的三点可以确定一个平面
D、两条相交直线可以确定一个平面1、下列命题中,正确的命题是( )A、圆上三点可以确定一个平面
B、圆心和圆上两点可确定一个平面
C、四条平行直线不能确定五个平面
D、空间四点中,若四点不共面,则任意三点不共线4、若给定空间三条直线共面的条件,这四个条
件中不正确的是( )①三条直线两两相交 ② 三条直线两两平行
③三条直线中有两条 ④平行三条直线共点3、在空间中,下列命题错误的是( )5、根据下列条件画出图形:平面α∩平面β=AB
直线a∈α,直线b∈β,a∥AB,b∥AB 6、如图、A∈α,直线AB和AC不在α内,画出AB和AC所确定的平面β,并画出直线BC和平面α的交点. 课时小结:
(师生互动,共同归纳)
(1)本节课我们学习了哪些知识内容?(2)三个公理的内容及作用是什么?
作业布置:
P52???习题2.1A组1、2题
2、会用符号表示出点与直线,点与平面,直线和平面以及平面与平面相交的位置关系;
3、掌握平面的基本性质(三个公理)及作用;
4、培养学生的空间想象能力。教学目标平面实物引入、揭示课题同学们观察长方体并思考以下问题:1、长方体由哪些基本元素构成?2、观察长方体的面,说说它的特点??答:点、线、面答: 长方体由上下、前后、左右六个面围成.它们都是平的。长方体的面给我们以平面的印象;生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的印象。实物引入、揭示课题1、平面的含义以上实物都给我们以平面的印象,几何里所说的平面,就是从这样的一些物体中抽象出来的。平面是没有厚薄的,可以无限延伸,这是平面最基本的属性。常见的桌面,黑板面,平静的水面等都是平面的局部形象;一个平面把空间分成两部分,一条直线把平面分成两部分2、平面的画法及表示①平面的画法:在立体几何中,常用平行四边形表示平面,当平面水平放置时,通常把平行四边形的锐角画成450,且横边长画成邻边长的两倍;画两个平面相交时,当一个平面的一部分被另一个平面遮住时,应把被遮住的部分画成虚线或不画。②、平面的表示方法平面 常把希腊字母α、β、γ等写在代表平面的平行四边形的一个角上,如平面α、平面β等;也可以用代表平面的四边形的四个顶点,或者相对的两个顶点的大写英文字母作为这个平面的名称.3、点、直线与平面的关系平面内有无数个点,平面可以看成点的集合.点A在平面α内,记作A∈α点B在平面α外,
记作B?α 直线l在平面α内表示为
l?α直线l不在平面α内表示为 l?α练习思考4、平面的基本性质如果直线 l 与平面α有一个公共点,直线 l 是否在平面α内?如果直线 l 与
平面α有两个公共点呢?实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.图形语言符号语言B··A·..公理1:如果一条直线上的两点在一个平面内,
那么这条直线在此平面内.用途:可以用来判断直线是否在平面内.4、平面的基本性质 在生产、生活中,人们经过长期观察与实践,总结出关于平面的一些基本性质,我们把它作为公理.这些公理是进一步推理的基础.生活中经常看到用三角架支撑照相机.或测量用的平板仪等等……4、平面的基本性质公理2 过不在一条直线上的三点,有且只有一个平面.存在性唯一性作用:
确定平面的主要依据. 不再一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.4、平面的基本性质补充3个推论:4、平面的基本性质推论1:经过一条直线与直线外一点,有且只有一个平面。
推论2:经过两条平行直线,有且只有一个平面。
推论3:经过两条相交直线,有且只有一个平面。 把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B ?为什么?思考4、平面的基本性质 观察长方体,你能发现长方体的两个相交平面有没有公共直线吗?观察 这条公共直线B’C’叫做这两个平面A’B’C’D’和平面BB’C’C的交线. 另一方面,相邻两个平面有一个公共点,如平面A’B’C’D’和平面BB’C’C有一个公共点B’,经过点B有且只有一条过该点的公共直线B’C’.4、平面的基本性质公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.②判断点在直线上.4、平面的基本性质符号表示为:图形表示为:例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.(1)(2)解:在(1)中,在(2)中,例题示范课堂练习:课本P44?练习1、2、3、4补练:①有三个公共点的两个平面重合
②梯形的四个顶点在同一个平面内
③三条互相平行的直线必共面
④ 四条线段顺次首尾连接,构成平面图形2、下列命题正确的是 ( )A、两条直线可以确定一个平面
B、一条直线和一个点可以确定一个平面
C、空间不同的三点可以确定一个平面
D、两条相交直线可以确定一个平面1、下列命题中,正确的命题是( )A、圆上三点可以确定一个平面
B、圆心和圆上两点可确定一个平面
C、四条平行直线不能确定五个平面
D、空间四点中,若四点不共面,则任意三点不共线4、若给定空间三条直线共面的条件,这四个条
件中不正确的是( )①三条直线两两相交 ② 三条直线两两平行
③三条直线中有两条 ④平行三条直线共点3、在空间中,下列命题错误的是( )5、根据下列条件画出图形:平面α∩平面β=AB
直线a∈α,直线b∈β,a∥AB,b∥AB 6、如图、A∈α,直线AB和AC不在α内,画出AB和AC所确定的平面β,并画出直线BC和平面α的交点. 课时小结:
(师生互动,共同归纳)
(1)本节课我们学习了哪些知识内容?(2)三个公理的内容及作用是什么?
作业布置:
P52???习题2.1A组1、2题
