(新人教a版必修2)数学:3.2直线的方程直线方程ppt
文档属性
| 名称 | (新人教a版必修2)数学:3.2直线的方程直线方程ppt |  | |
| 格式 | rar | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-08 09:51:00 | ||
图片预览








文档简介
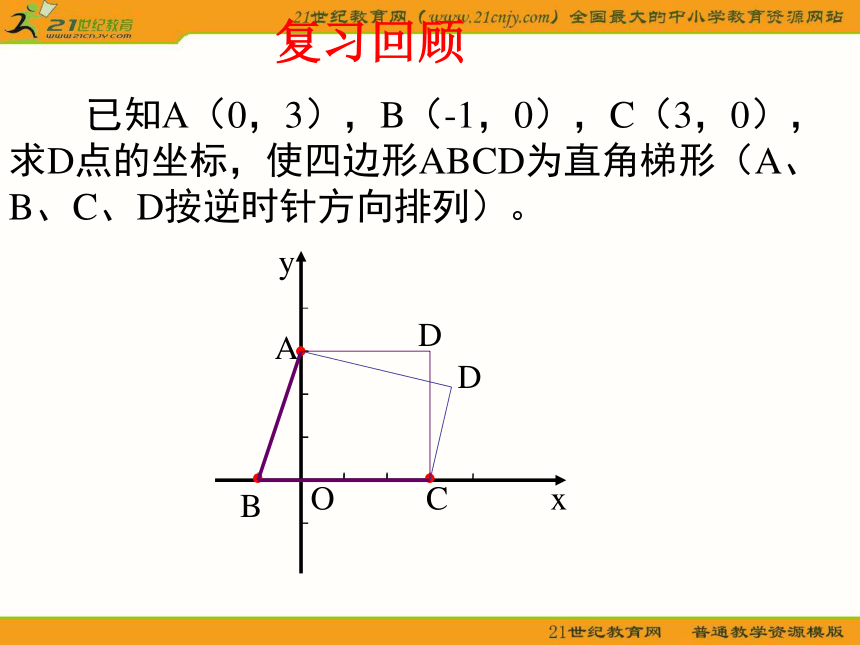
课件23张PPT。3.2.1 直线的点斜式方程复习回顾 已知A(0,3),B(-1,0),C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列)。1、直线的点斜式方程:已知直线l经过已知点P1(x1,y1),并且它的斜率是k
求直线l的方程。Oxyl 设点P(x,y)是直线l上
不同于P1的任意一点。
根据经过两点的直线斜率
公式,得由直线上一点和直线的斜率确定的直线方程,叫直线的点斜式方程。新课:小结:直线上任意一点P与这条直线上
一个定点P1所确定的斜率都相等。⑵当P点与P1重合时,有x=x1,y=y1,此时满足y-y1=k(x
-x1),所以直线l上所有点的坐标都满足y-y1=k(x-x1),
而不在直线l上的点,显然不满足(y-y1)/(x-x1)=k即
不满足y-y1=k(x-x1),因此y-y1=k(x-x1)是直线l的方程。 如果直线l过P1且平行于Y轴,此时它的
倾斜角是900,而它的斜率不存在,它的方程不能用点斜
式表示,但这时直线上任一点的横坐标x都等于P1的横坐
标所以方程为x=x1⑶如直线l过P1且平行于x轴,则它的斜率k=0,由点斜式
知方程为y=y0;⑴P为直线上的任意一点,它的
位置与方程无关Oxy°P1°°°°°°°P°°°°°°应用:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这
条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2, 即x-y + 5 = 0Oxy-55°P1例2:一条直线经过点A(0,5),倾斜角为00,求这直线方程解:这条直线经过点A(0,5)
斜率是k=tan00=0代入点斜式,得y - 5 = 0Oxy5°°②直线的斜截式方程:已知直线l的斜率是k,与y轴的交点是P(0,b),求
直线方程。代入点斜式方程,得l的直线方程:y - b =k ( x - 0)即 y = k x + b 。 (2)例3:斜率是5,在y轴上的截距是4的直线方程。解:由已知得k =5, b= 4,代入斜截式方程y= 5x + 4 即5 x - y + 4 = 0㈢巩固:
①经过点(- ,2)倾斜角是300的直线的方程是
(A)y+ = ( x-2) (B)y+2= (x- )
(C)y-2= (x+ )(D)y-2= (x+ )
②已知直线方程y-3= (x-4),则这条直线经过的已知
点,倾斜角分别是
(A)(4,3);π/ 3 (B)(-3,-4);π/ 6
(C)(4,3);π/ 6 (D)(-4,-3);π/ 3
③直线方程可表示成点斜式方程的条件是
(A)直线的斜率存在 (B)直线的斜率不存在
(C)直线不过原点 (D)不同于上述答案
㈣总结:
①直线的点斜式,斜截式方程在直线
斜率存在时才可以应用。
②直线方程的最后形式应表示成
二元一次方程的一般形式。 §3.2.2 直线的两点式方程课前提问: 若直线l经过点P1(1,2), P2(3,5),
求直线l的方程.直线方程的两点式 已知直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2, y1≠y2 ),如何求出通过这两点的直线方程呢?思考: 经过直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2, y1≠y2 )的直线方程叫做直线的两点式方程,简称两点式。说明(1)这个方程由直线上两点确定;
(2)当直线没有斜率或斜率为0时,不能用
两点式求出它们的方程.(此时方程如何得到?)例题分析例1、已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求这条直线l的方程.说明: (1)直线与x轴的交点(a,0)的横坐标a叫做直线在x轴的截距,此时直线在y轴的截距是b; x l B A O y(3)截距式适用于横、纵截距都存在且都不为0的直线.(2)这个方程由直线在x轴和y轴的截距确定,所以叫做直线方程的截距式方程;例2、三角形的顶点是A(-5,0),B(3,-3),C(0,2),
求BC边所在直线的方程,以及该边上中线所在直线的方程.补充练习 已知两点A(-3,4),B(3, 2),过点P(2,-1)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围
(2)求直线l的倾斜角α的取值范围补充练习 §3.2.3直线的一般式方程温故知新复习回顾①直线方程有几种形式?指明它们的条件及应用范围.点斜式y-y1 = k(x-x1)斜截式y = kx + b两点式截距式②什么叫二元一次方程?直线与二元一次方程有什么关系?例题分析直线的一般式方程:Ax+By+C=0(A,B不同时为0)注意 对于直线方程的一般式,一般作如下约定:x的系数为正,x,y的系数及常数项一般不出现分数,一般按含x项,含y项、常数项顺序排列.例2、把直线l 的方程x –2y+6= 0化成斜截式,求出
直线l 的斜率和它在x轴与y轴上的截距,并画图.例题分析例3、设直线l 的方程为
(m2-2m-3)x+(2m2+m-1)y=2m-6,根据下列
条件确定m的值:
(1) l 在X轴上的截距是-3;
(2)斜率是-1.例4、利用直线方程的一般式,求过点(0,3)并且
与坐标轴围成三角形面积是6的直线方程.练习:
1、直线Ax+By+C=0通过第一、二、三象限,则( )
(A) A·B>0,A·C>0 (B) A·B>0,A·C<0
(C) A·B<0,A·C>0 (D) A·B<0,A·C<0例题分析2、设A、B是x轴上的两点,点P的横坐标为2,且│PA│=│PB│,若直线PA的方程为x-y+1=0,则直线PB的方程是( )
A.2y-x-4=0 B.2x-y-1=0
C.x+y-5=0 D.2x+y-7=0
求直线l的方程。Oxyl 设点P(x,y)是直线l上
不同于P1的任意一点。
根据经过两点的直线斜率
公式,得由直线上一点和直线的斜率确定的直线方程,叫直线的点斜式方程。新课:小结:直线上任意一点P与这条直线上
一个定点P1所确定的斜率都相等。⑵当P点与P1重合时,有x=x1,y=y1,此时满足y-y1=k(x
-x1),所以直线l上所有点的坐标都满足y-y1=k(x-x1),
而不在直线l上的点,显然不满足(y-y1)/(x-x1)=k即
不满足y-y1=k(x-x1),因此y-y1=k(x-x1)是直线l的方程。 如果直线l过P1且平行于Y轴,此时它的
倾斜角是900,而它的斜率不存在,它的方程不能用点斜
式表示,但这时直线上任一点的横坐标x都等于P1的横坐
标所以方程为x=x1⑶如直线l过P1且平行于x轴,则它的斜率k=0,由点斜式
知方程为y=y0;⑴P为直线上的任意一点,它的
位置与方程无关Oxy°P1°°°°°°°P°°°°°°应用:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这
条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2, 即x-y + 5 = 0Oxy-55°P1例2:一条直线经过点A(0,5),倾斜角为00,求这直线方程解:这条直线经过点A(0,5)
斜率是k=tan00=0代入点斜式,得y - 5 = 0Oxy5°°②直线的斜截式方程:已知直线l的斜率是k,与y轴的交点是P(0,b),求
直线方程。代入点斜式方程,得l的直线方程:y - b =k ( x - 0)即 y = k x + b 。 (2)例3:斜率是5,在y轴上的截距是4的直线方程。解:由已知得k =5, b= 4,代入斜截式方程y= 5x + 4 即5 x - y + 4 = 0㈢巩固:
①经过点(- ,2)倾斜角是300的直线的方程是
(A)y+ = ( x-2) (B)y+2= (x- )
(C)y-2= (x+ )(D)y-2= (x+ )
②已知直线方程y-3= (x-4),则这条直线经过的已知
点,倾斜角分别是
(A)(4,3);π/ 3 (B)(-3,-4);π/ 6
(C)(4,3);π/ 6 (D)(-4,-3);π/ 3
③直线方程可表示成点斜式方程的条件是
(A)直线的斜率存在 (B)直线的斜率不存在
(C)直线不过原点 (D)不同于上述答案
㈣总结:
①直线的点斜式,斜截式方程在直线
斜率存在时才可以应用。
②直线方程的最后形式应表示成
二元一次方程的一般形式。 §3.2.2 直线的两点式方程课前提问: 若直线l经过点P1(1,2), P2(3,5),
求直线l的方程.直线方程的两点式 已知直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2, y1≠y2 ),如何求出通过这两点的直线方程呢?思考: 经过直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2, y1≠y2 )的直线方程叫做直线的两点式方程,简称两点式。说明(1)这个方程由直线上两点确定;
(2)当直线没有斜率或斜率为0时,不能用
两点式求出它们的方程.(此时方程如何得到?)例题分析例1、已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求这条直线l的方程.说明: (1)直线与x轴的交点(a,0)的横坐标a叫做直线在x轴的截距,此时直线在y轴的截距是b; x l B A O y(3)截距式适用于横、纵截距都存在且都不为0的直线.(2)这个方程由直线在x轴和y轴的截距确定,所以叫做直线方程的截距式方程;例2、三角形的顶点是A(-5,0),B(3,-3),C(0,2),
求BC边所在直线的方程,以及该边上中线所在直线的方程.补充练习 已知两点A(-3,4),B(3, 2),过点P(2,-1)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围
(2)求直线l的倾斜角α的取值范围补充练习 §3.2.3直线的一般式方程温故知新复习回顾①直线方程有几种形式?指明它们的条件及应用范围.点斜式y-y1 = k(x-x1)斜截式y = kx + b两点式截距式②什么叫二元一次方程?直线与二元一次方程有什么关系?例题分析直线的一般式方程:Ax+By+C=0(A,B不同时为0)注意 对于直线方程的一般式,一般作如下约定:x的系数为正,x,y的系数及常数项一般不出现分数,一般按含x项,含y项、常数项顺序排列.例2、把直线l 的方程x –2y+6= 0化成斜截式,求出
直线l 的斜率和它在x轴与y轴上的截距,并画图.例题分析例3、设直线l 的方程为
(m2-2m-3)x+(2m2+m-1)y=2m-6,根据下列
条件确定m的值:
(1) l 在X轴上的截距是-3;
(2)斜率是-1.例4、利用直线方程的一般式,求过点(0,3)并且
与坐标轴围成三角形面积是6的直线方程.练习:
1、直线Ax+By+C=0通过第一、二、三象限,则( )
(A) A·B>0,A·C>0 (B) A·B>0,A·C<0
(C) A·B<0,A·C>0 (D) A·B<0,A·C<0例题分析2、设A、B是x轴上的两点,点P的横坐标为2,且│PA│=│PB│,若直线PA的方程为x-y+1=0,则直线PB的方程是( )
A.2y-x-4=0 B.2x-y-1=0
C.x+y-5=0 D.2x+y-7=0
