(新人教a版必修2)数学:4.2《直线、圆的位置关系》课件(10)
文档属性
| 名称 | (新人教a版必修2)数学:4.2《直线、圆的位置关系》课件(10) |

|
|
| 格式 | rar | ||
| 文件大小 | 509.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-08 00:00:00 | ||
图片预览







文档简介
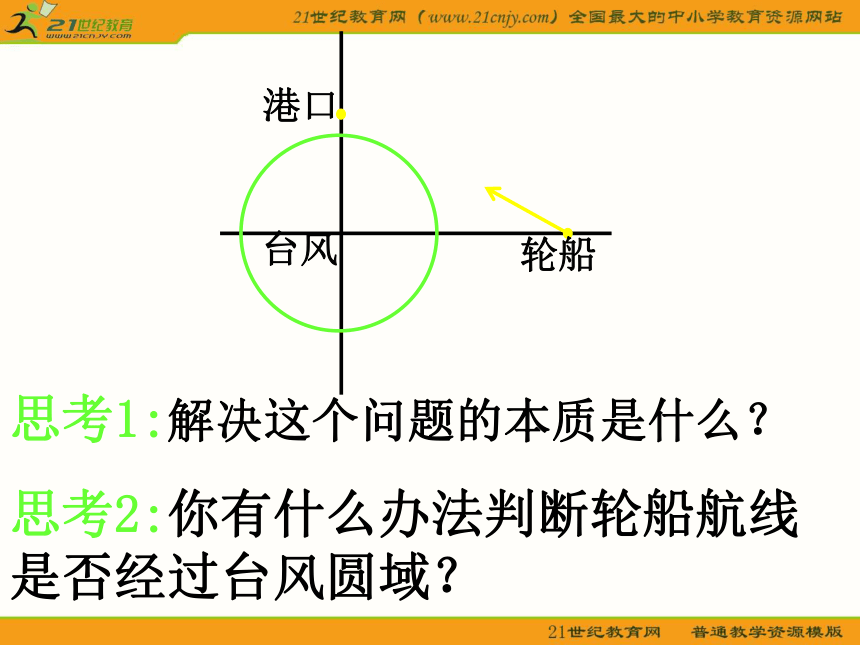
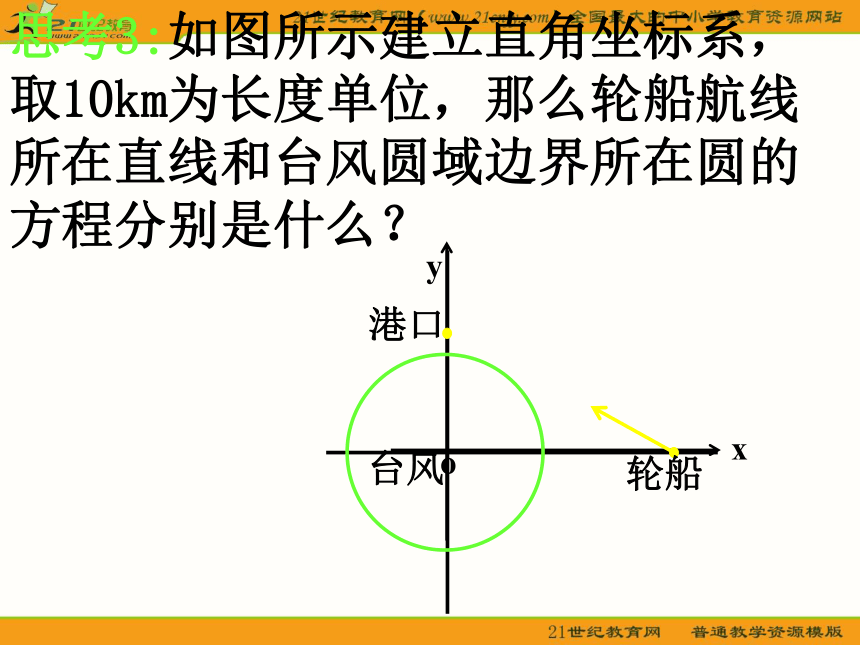
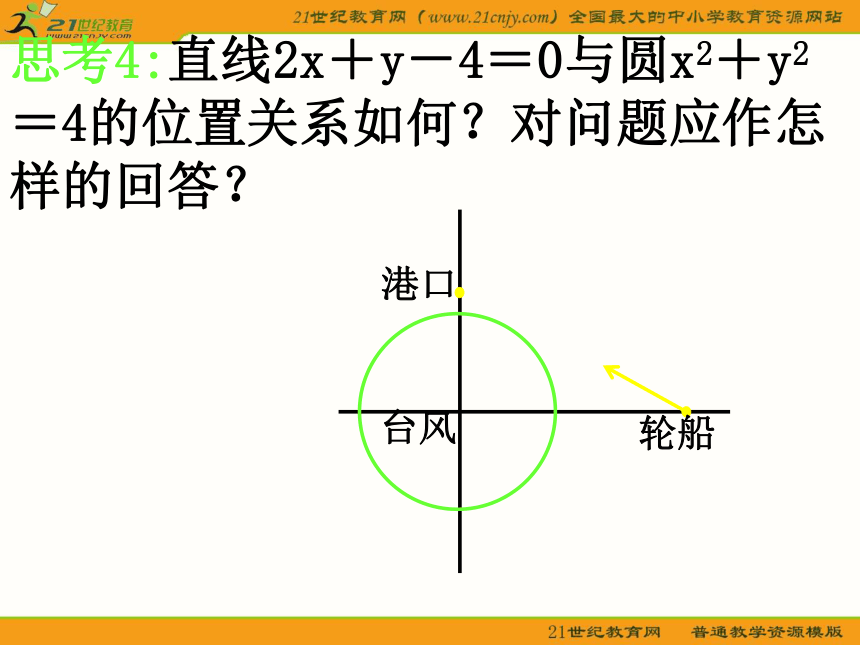
课件53张PPT。 创设情境 引入新课 一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西40 km处, 受影响的范围是半径长为20km的圆形区域. 已知港口位于台风中心正北20 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?思考1:解决这个问题的本质是什么?思考2:你有什么办法判断轮船航线是否经过台风圆域?思考3:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?思考4:直线2x+y-4=0与圆x2+y2=4的位置关系如何?对问题应作怎样的回答?第一课时直线与圆的位置关系直线方程的一般式为:____________________________2.圆的标准方程为______________3.圆的一般方程:__________________________________ 复习圆心为________半径为______Ax+By+C=0(A,B不同时为零)(x-a)2+(y-b)2=r2x2+y2+Dx+Ey+F=0(其中D2+E2-4F>0)
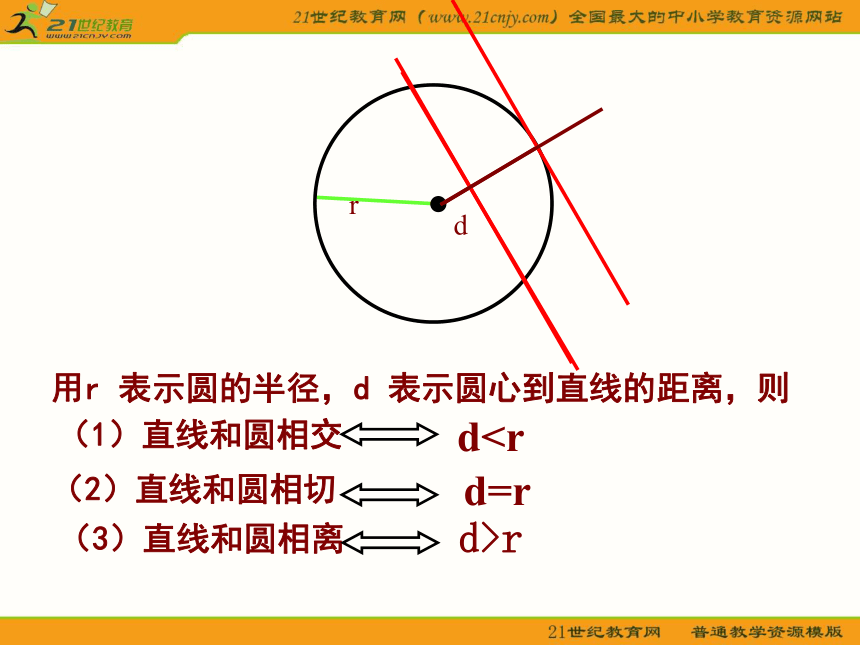
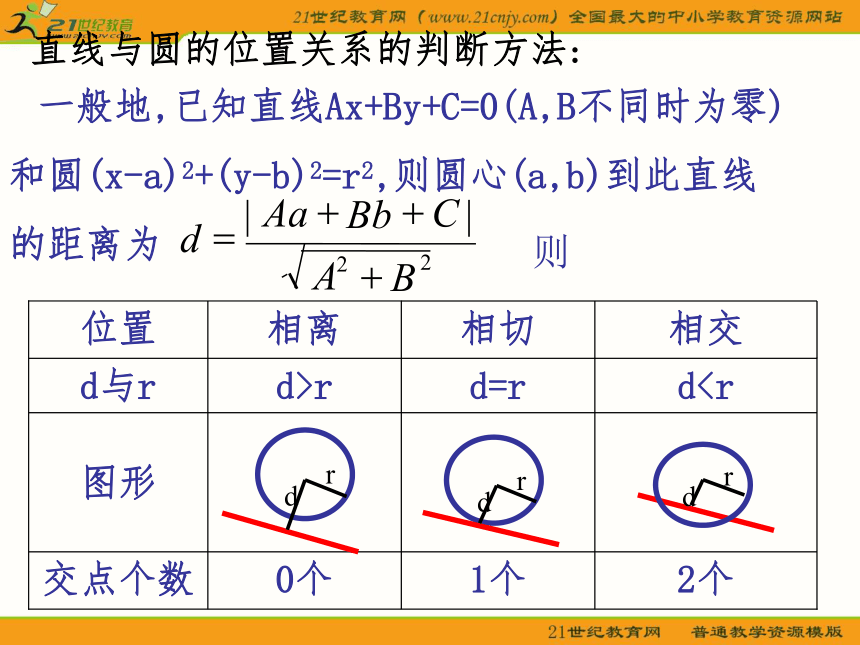
圆心为 半径为(a,b)r问题1:你知道直线和圆的位置关系有几种?演示用r 表示圆的半径,d 表示圆心到直线的距离,则r直线与圆的位置关系的判断方法:则 一般地,已知直线Ax+By+C=0(A,B不同时为零)
和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线
的距离为问题2:平面直角坐标系中,怎样根据方程来判断直线与圆的位置关系?设直线l方程为:Ax+By+C=0,
圆C的方程为: x2+y2+Dx+Ey+F=0例1:直线2x+y-4=0与圆x2+y2=4的位置关系如何?2.直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置是________。相交1.直线x+y-2=0与圆x2+y2=2的位置关系为________。相切尝试一下例2 :求满足下列条件的各圆C的方程:
(1)圆心为(0,0),且与直线4x+3y-15=0相切;
(2)圆心在直线y=x上,与两轴同时相切,半径为2; (3)圆心在y轴上,且与直线x+2y-3=0相切于点(-1,2).(x-2)2+(y-2)2=4 或 (x+2)2+(y+2)2=4(2)求圆心在直线y = x上,与两轴同时相切,半径为2的圆的方程.小结:利用圆的标准方程解题需要确定圆的圆心和半径.(3)求圆心在y轴上,且与直线x+2y-3=0相切于点A(-1,2)的圆的方程.例3:自点A(-3,3)发射的光线l 射到x轴上,被x轴反射,
其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,
求反射光线所在直线的方程
?B(-3,-3)注意:利用斜率研究直线时,要注意直线斜率不存在的情形,应通过检验,判断它是否符合题意。 直线l过点A(1,0)且与圆(x-2)2+(y-3)2=1相切,求直线l的方程。 师生互动小结探究一下巩固练习:练习册P113-11请同学们谈谈这节课学到了什么东西。学完一节课或一个内容,
应当及时小结,梳理知识学习必杀技:小结:判断直线和圆的位置关系几何方法求圆心坐标及半径r(配方法) 圆心到直线的距离d (点到直线距离公式)代数方法 消去y(或x)作业:
P132习题4.2A组:1,2.
P144复习题B组:1,5. 第二课时直线与圆的位置关系1、判定直线 与圆的位置关系的方法有两种
(1)代数方法,由直线 与圆的公共点 的个数来判断
(2)几何方法,由圆心到直线的距离d与半径r的关系判断。
在实际应用中,常采用第二种方法判定。 2、利用斜率研究直线时,要注意直线斜率不存在的情形,应通过检验,判断它是否符合题意。 已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系。(课本P127-例7)师生互动问题:若设直线与圆相交于A,B两点,
求弦长|AB|的值.ABABDrd方法小结求圆的弦长方法
(1)几何法:用弦心距,半径及半弦构成直角三角形的三边
(2)代数法:求交点坐标用距离公式求解 例1:一圆与y轴相切,圆心在直线
x-3y=0上,在y=x上截得弦长为 ,求此圆的方程。解:设该圆的方程是(x-3b)2+(y-b)2=9b2, 圆心(3b,b)到直线x-y=0的距离是故所求圆的方程是(x-3)2+(y-1)2=9
或(x+3)2+(y+1)2=9。r=|3b|1.恒过定点P(3,2)2.直线l过P且垂直于CP时,弦长最小.1.已知直线2x-y+3=0和圆x2+y2+4y-21=0相交于A,B两点,则|AB|=_____.尝试一下2.点(-3,-3)是圆x2+y2+4y-21=0的一条弦的中点,则这条弦所在的直线方程是___.3.已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为 ,则直线l的方程是___________.小结 一只小老鼠在圆(x-5)2+(y-3)2=9上环
行,它走到哪个位置时与直线l :
3x+4y-2=0的距离最短,请你帮小老鼠找
到这个点并计算这个点到直线l的距离。 请你来帮忙小结演
示解探究一下请同学们谈谈这节课学到了什么东西。学完一节课或一个内容,
应当及时小结,梳理知识学习必杀技:作业
P132-133习题4.2A组:5,6.
B组: 4.
P144复习题B组:4,6. 第三课时圆与圆的位置关系 前面我们运用直线与圆的方程,研究了直线与圆的位置关系.现在我们运用圆的方程,研究点与圆,圆与圆的位置关系.OArOA=r 在直角坐标系中,已知点
M(x0,y0)和圆C: ,如何判断点M在圆外、圆上、圆内?(x0-a)2+(y0-b)2>r2时,点M在圆C外;(x0-a)2+(y0-b)2=r2时,点M在圆C上;(x0-a)2+(y0-b)2点M在圆x2+y2-4x+2y+4=0
上运动,求|PM|的最大
值和最小值.圆心C(2,-1),半径r=1|PM|max=|PC|+r=6 |PM|min=|PC|-r=4 外离圆和圆的五种位置关系|O1O2|>|R+r||O1O2|=|R+r||R-r|<|O1O2|<|R+r||O1O2|=|R-r|0≤|O1O2|<|R-r||O1O2|=0外切相交内切内含同心圆(一种特殊的内含)判断两圆位置关系几何方法两圆心坐标及半径(配方法) 圆心距d
(两点间距离公式) 比较d和r1,r2的大小,下结论外离d>R+rd=R+rR-r(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法?判断C1和C2的位置关系判断C1和C2的位置关系解:联立两个方程组得①-②得把上式代入①①
②④所以方程④有两个不相等的实根x1,x2把x1,x2代入方程③得到y1,y2③所以圆C1与圆C2有两个不同的交点A(x1,y1),B(x2,y2)
联立方程组消去二次项消元得一元二次方程用Δ判断两圆的位置关系小结:判断两圆位置关系几何方法两圆心坐标及半径(配方法) 圆心距d
(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法 消去y(或x)判断C1和C2的位置关系解:联立两个方程组得①-②得把上式代入①①
②④所以方程④有两个不相等的实根x1,x2把x1,x2代入方程③得到y1,y2③所以圆C1与圆C2有两个不同的交点A(x1,y1),B(x2,y2)
两圆公共弦所在的直线方程圆系方程
过圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0的交点的圆的方程:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0 (λ≠-1) 当λ=-1时,表示两圆的公共弦所在的直线方程.2. 过圆C:x2+y2+Dx+Ey+F=0与直线l:Ax+By+C=0的交点的圆的方程:x2+y2+Dx+Ey+F+λ(Ax+By+C)=0 例3:
(1) 求圆心在x-y-4=0上,并且经过两圆C1: x2+y2-4x-3=0和C2: x2+y2-4y-3=0的交点的圆的方程;
(3) 经过两圆C1: x2+y2-4x-3=0和C2: x2+y2-4y-3=0的交点的公共弦直线方程
(4)过直线3x-4y-7=0和圆(x-2)2+(y+1)2=4的交点且过点(1,2)的圆的方程 师生互动G 求经过点M(3,-1) ,且与圆
切于点N(1,2)的圆的方程.(课本P133-11)yOCMNxD探究一下类比猜想
作业
P133习题B组: 5.
练习册P116-117:4,7,9,10,13.
圆心为 半径为(a,b)r问题1:你知道直线和圆的位置关系有几种?演示用r 表示圆的半径,d 表示圆心到直线的距离,则r直线与圆的位置关系的判断方法:则 一般地,已知直线Ax+By+C=0(A,B不同时为零)
和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线
的距离为问题2:平面直角坐标系中,怎样根据方程来判断直线与圆的位置关系?设直线l方程为:Ax+By+C=0,
圆C的方程为: x2+y2+Dx+Ey+F=0例1:直线2x+y-4=0与圆x2+y2=4的位置关系如何?2.直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置是________。相交1.直线x+y-2=0与圆x2+y2=2的位置关系为________。相切尝试一下例2 :求满足下列条件的各圆C的方程:
(1)圆心为(0,0),且与直线4x+3y-15=0相切;
(2)圆心在直线y=x上,与两轴同时相切,半径为2; (3)圆心在y轴上,且与直线x+2y-3=0相切于点(-1,2).(x-2)2+(y-2)2=4 或 (x+2)2+(y+2)2=4(2)求圆心在直线y = x上,与两轴同时相切,半径为2的圆的方程.小结:利用圆的标准方程解题需要确定圆的圆心和半径.(3)求圆心在y轴上,且与直线x+2y-3=0相切于点A(-1,2)的圆的方程.例3:自点A(-3,3)发射的光线l 射到x轴上,被x轴反射,
其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,
求反射光线所在直线的方程
?B(-3,-3)注意:利用斜率研究直线时,要注意直线斜率不存在的情形,应通过检验,判断它是否符合题意。 直线l过点A(1,0)且与圆(x-2)2+(y-3)2=1相切,求直线l的方程。 师生互动小结探究一下巩固练习:练习册P113-11请同学们谈谈这节课学到了什么东西。学完一节课或一个内容,
应当及时小结,梳理知识学习必杀技:小结:判断直线和圆的位置关系几何方法求圆心坐标及半径r(配方法) 圆心到直线的距离d (点到直线距离公式)代数方法 消去y(或x)作业:
P132习题4.2A组:1,2.
P144复习题B组:1,5. 第二课时直线与圆的位置关系1、判定直线 与圆的位置关系的方法有两种
(1)代数方法,由直线 与圆的公共点 的个数来判断
(2)几何方法,由圆心到直线的距离d与半径r的关系判断。
在实际应用中,常采用第二种方法判定。 2、利用斜率研究直线时,要注意直线斜率不存在的情形,应通过检验,判断它是否符合题意。 已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系。(课本P127-例7)师生互动问题:若设直线与圆相交于A,B两点,
求弦长|AB|的值.ABABDrd方法小结求圆的弦长方法
(1)几何法:用弦心距,半径及半弦构成直角三角形的三边
(2)代数法:求交点坐标用距离公式求解 例1:一圆与y轴相切,圆心在直线
x-3y=0上,在y=x上截得弦长为 ,求此圆的方程。解:设该圆的方程是(x-3b)2+(y-b)2=9b2, 圆心(3b,b)到直线x-y=0的距离是故所求圆的方程是(x-3)2+(y-1)2=9
或(x+3)2+(y+1)2=9。r=|3b|1.恒过定点P(3,2)2.直线l过P且垂直于CP时,弦长最小.1.已知直线2x-y+3=0和圆x2+y2+4y-21=0相交于A,B两点,则|AB|=_____.尝试一下2.点(-3,-3)是圆x2+y2+4y-21=0的一条弦的中点,则这条弦所在的直线方程是___.3.已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为 ,则直线l的方程是___________.小结 一只小老鼠在圆(x-5)2+(y-3)2=9上环
行,它走到哪个位置时与直线l :
3x+4y-2=0的距离最短,请你帮小老鼠找
到这个点并计算这个点到直线l的距离。 请你来帮忙小结演
示解探究一下请同学们谈谈这节课学到了什么东西。学完一节课或一个内容,
应当及时小结,梳理知识学习必杀技:作业
P132-133习题4.2A组:5,6.
B组: 4.
P144复习题B组:4,6. 第三课时圆与圆的位置关系 前面我们运用直线与圆的方程,研究了直线与圆的位置关系.现在我们运用圆的方程,研究点与圆,圆与圆的位置关系.OA
M(x0,y0)和圆C: ,如何判断点M在圆外、圆上、圆内?(x0-a)2+(y0-b)2>r2时,点M在圆C外;(x0-a)2+(y0-b)2=r2时,点M在圆C上;(x0-a)2+(y0-b)2
上运动,求|PM|的最大
值和最小值.圆心C(2,-1),半径r=1|PM|max=|PC|+r=6 |PM|min=|PC|-r=4 外离圆和圆的五种位置关系|O1O2|>|R+r||O1O2|=|R+r||R-r|<|O1O2|<|R+r||O1O2|=|R-r|0≤|O1O2|<|R-r||O1O2|=0外切相交内切内含同心圆(一种特殊的内含)判断两圆位置关系几何方法两圆心坐标及半径(配方法) 圆心距d
(两点间距离公式) 比较d和r1,r2的大小,下结论外离d>R+rd=R+rR-r
②④所以方程④有两个不相等的实根x1,x2把x1,x2代入方程③得到y1,y2③所以圆C1与圆C2有两个不同的交点A(x1,y1),B(x2,y2)
联立方程组消去二次项消元得一元二次方程用Δ判断两圆的位置关系小结:判断两圆位置关系几何方法两圆心坐标及半径(配方法) 圆心距d
(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法 消去y(或x)判断C1和C2的位置关系解:联立两个方程组得①-②得把上式代入①①
②④所以方程④有两个不相等的实根x1,x2把x1,x2代入方程③得到y1,y2③所以圆C1与圆C2有两个不同的交点A(x1,y1),B(x2,y2)
两圆公共弦所在的直线方程圆系方程
过圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0的交点的圆的方程:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0 (λ≠-1) 当λ=-1时,表示两圆的公共弦所在的直线方程.2. 过圆C:x2+y2+Dx+Ey+F=0与直线l:Ax+By+C=0的交点的圆的方程:x2+y2+Dx+Ey+F+λ(Ax+By+C)=0 例3:
(1) 求圆心在x-y-4=0上,并且经过两圆C1: x2+y2-4x-3=0和C2: x2+y2-4y-3=0的交点的圆的方程;
(3) 经过两圆C1: x2+y2-4x-3=0和C2: x2+y2-4y-3=0的交点的公共弦直线方程
(4)过直线3x-4y-7=0和圆(x-2)2+(y+1)2=4的交点且过点(1,2)的圆的方程 师生互动G 求经过点M(3,-1) ,且与圆
切于点N(1,2)的圆的方程.(课本P133-11)yOCMNxD探究一下类比猜想
作业
P133习题B组: 5.
练习册P116-117:4,7,9,10,13.
