(新人教b版必修2)数学: 第一章 立体几何初步(章综合)
文档属性
| 名称 | (新人教b版必修2)数学: 第一章 立体几何初步(章综合) |  | |
| 格式 | rar | ||
| 文件大小 | 86.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-09 09:11:00 | ||
图片预览


文档简介
新课标苏教版高中数学必修2第一章
《立体几何初步》过关测试卷
( 时间 120分钟 总分 150分)
班级_______________ 姓名______________ 分数_____________
一、选择题(每小题5分,共60分)
1、下列四个结论:⑴两条直线都和同一个平面平行,则这两条直线平行。⑵两条直线没有公共点,则这两条直线平行。⑶两条直线都和第三条直线垂直,则这两条直线平行。⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行。其中正确的个数为
A 0 B 1 C 2 D 3
2、棱台上、下底面面积之比为1∶9,则棱台的中截面分棱台成两部分的体积之比是
A 1∶7 B 2∶7 C 7∶19 D 5∶ 16
3、一个正方体的顶点都在球面上,它的棱长为2cm,则球的表面积是
A B C D
4、已知直线∥平面,,那么过点且平行于的直线
A 只有一条,不在平面内 B 只有一条,在平面内
C 有两条,不一定都在平面内 D 有无数条,不一定都在平面内
5、下列四个命题正确的是
A 两两相交的三条直线必在同一平面内 B 若四点不共面,则其中任意三点都不共线
C 在空间中,四边相等的四边形是菱形 D 在空间中,有三个角是直角的四边形是矩形
6、若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积的比为
A 1:2:3 B 2:3:4 C 3:2:4 D 3:1:2
7、某玻璃制品公司需要生产棱长均为3cm的玻璃三棱柱一批。请问每个三棱柱需要用玻璃多少cm 3 ?
A B C D
8、下列说法中正确的是
A 经过两条平行直线,有且只有一个平面直线
B 如果两条直线同平行于同一个平面,那么这两条直线平行
C 三点唯一确定一个平面
D 不在同一平面内的两条直线相互垂直,则这两个平面也相互垂直
9、把两半径为2的铁球熔化成一个球,则这个大球的半径应为
A 4 B C D
10、线和平面,能得出的一个条件是
A B
C D
11、线a、b和平面,下面推论错误的是
A. B
C D
12、设m、n是两条不同的直线,是三个不同的平面,给出下列四个命题:
①若,,则 ②若,,,则
③若,,则 ④若,,则
其中正确命题的序号是
A ①和② B ②和③ C ③和④ D ①和④
二、填空题(每小题4分,共16分)
13、已知圆锥的表面积为6,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为_______________.
14、用一张圆弧长等于12分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于 ______________立方分米.
15、设是外一点,则使点在此三角形所在平面内的射影是的垂心的条件为________________________(填一种即可).
16、已知直线是直线,是平面,给出下列命题:[来源:21世纪教育网]
① ,则;
② ,则;
③ ,则;
④ ,则.
其中正确命题的序号
选择题答题卡
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
三、解答题(共74分)
17、(本题12分)正四棱台的高是8cm,两底面的边长分别为4cm和16cm,求这个棱台的侧棱的长、斜高、表面积、体积.
18、(本题12分)三棱锥V—ABC中,VO⊥平面ABC, O∈CD , VA=VB,AD=BD.
证明:CD⊥AB且AC=BC .
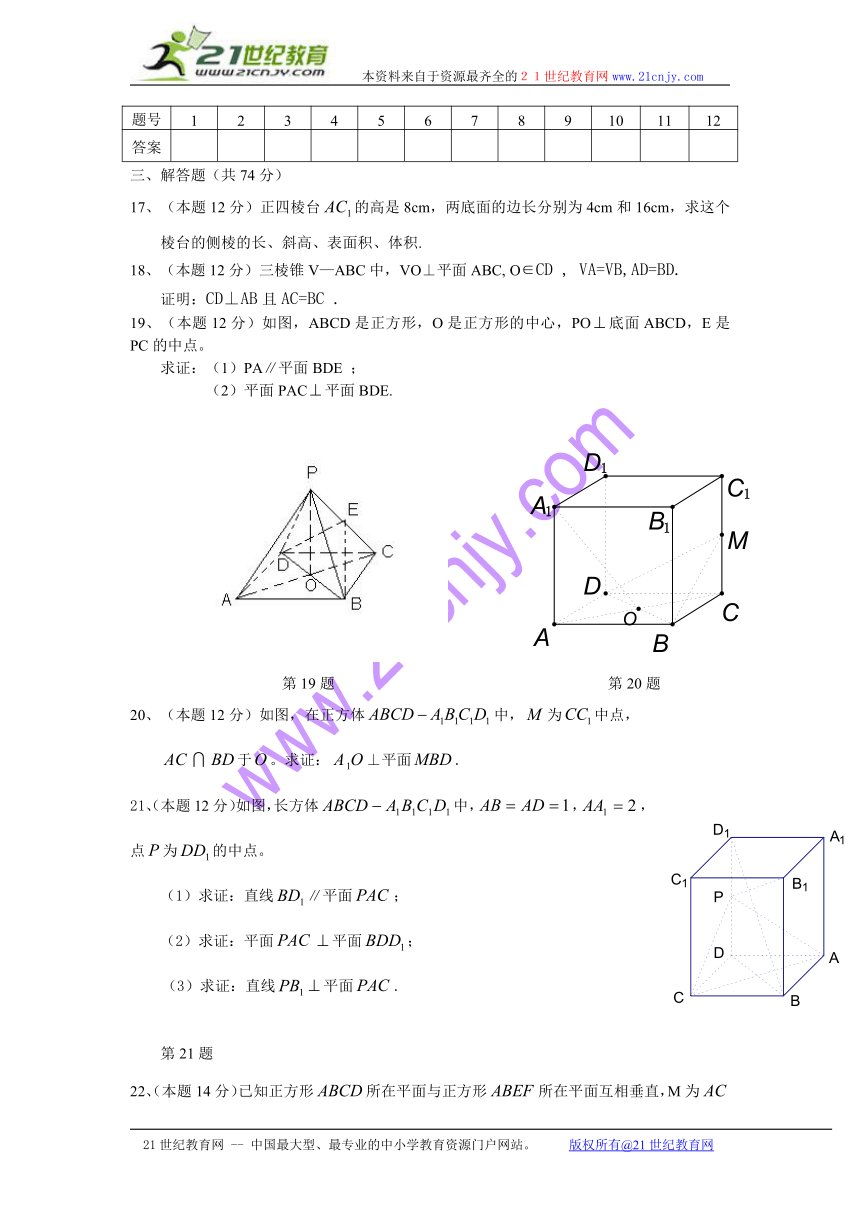
19、(本题12分)如图,ABCD是正方形,O是正方形的中心,PO底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE ;
(2)平面PAC平面BDE.21世纪教育网
第19题 第20题
20、(本题12分)如图,在正方体中,为中点,
于。求证:⊥平面.21世纪教育网
21、(本题12分)如图,长方体中,,,点为的中点。
(1)求证:直线∥平面;
(2)求证:平面平面;
(3)求证:直线平面.
第21题
22、(本题14分)已知正方形所在平面与正方形所在平面互相垂直,M为上一点,N为 上一点,且有,设
(1) 求证:;
(2) 求证: ;
(3) 当为何值时,取最小值?并求出这个最小值.
参考答案
1-12题 ACBBB DDACC DA; 13、;14、96;15、 ; 16、①③④
17、解:如图:连结两底面中心,并连结和,
过作于,则为高,[来源:21世纪教育网]
为斜高,
在中,cm,
在中,cm,
cm
cm
棱台的侧棱长为cm,斜高为10 cm,表面积为672 cm,体积为896 cm
18、证:
19、证明(1)∵O是AC的中点,E是PC的中点,∴OE∥AP,
又∵OE平面BDE,PA平面BDE,∴PA∥平面BDE
(2)∵PO底面ABCD,∴POBD,又∵ACBD,且ACPO=O
∴BD平面PAC,而BD平面BDE,∴平面PAC平面BDE。
20、略
21、解:(1)设AC和BD交于点O,连PO,
由P,O分别是,BD的中点,故PO//,
所以直线∥平面--(4分)
(2)长方体中,,
底面ABCD是正方形,则ACBD
又面ABCD,则AC,
所以AC面,则平面平面
(3)PC2=2,PB12=3,B1C2=5,所以△PB1C是直角三角形。PC,
同理PA,所以直线平面。--(14分)
22、证明:(1) 在平面ABC中,作,在平面BFE中,作,连结GH
MNHG为平行四边形;
又GH面BEC,MN面BEC
MN//面BEC
(2)
AB面BEC
GH面GEC ABGH
MN//GH MNAB21世纪教育网
(3) 面ABCD面ABEF
BE面ABCD BEBC
BG= , BH=
MN=GH==
=()
= 当且仅当时,等号成立;
当时,MN取最小值.
《立体几何初步》过关测试卷
( 时间 120分钟 总分 150分)
班级_______________ 姓名______________ 分数_____________
一、选择题(每小题5分,共60分)
1、下列四个结论:⑴两条直线都和同一个平面平行,则这两条直线平行。⑵两条直线没有公共点,则这两条直线平行。⑶两条直线都和第三条直线垂直,则这两条直线平行。⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行。其中正确的个数为
A 0 B 1 C 2 D 3
2、棱台上、下底面面积之比为1∶9,则棱台的中截面分棱台成两部分的体积之比是
A 1∶7 B 2∶7 C 7∶19 D 5∶ 16
3、一个正方体的顶点都在球面上,它的棱长为2cm,则球的表面积是
A B C D
4、已知直线∥平面,,那么过点且平行于的直线
A 只有一条,不在平面内 B 只有一条,在平面内
C 有两条,不一定都在平面内 D 有无数条,不一定都在平面内
5、下列四个命题正确的是
A 两两相交的三条直线必在同一平面内 B 若四点不共面,则其中任意三点都不共线
C 在空间中,四边相等的四边形是菱形 D 在空间中,有三个角是直角的四边形是矩形
6、若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积的比为
A 1:2:3 B 2:3:4 C 3:2:4 D 3:1:2
7、某玻璃制品公司需要生产棱长均为3cm的玻璃三棱柱一批。请问每个三棱柱需要用玻璃多少cm 3 ?
A B C D
8、下列说法中正确的是
A 经过两条平行直线,有且只有一个平面直线
B 如果两条直线同平行于同一个平面,那么这两条直线平行
C 三点唯一确定一个平面
D 不在同一平面内的两条直线相互垂直,则这两个平面也相互垂直
9、把两半径为2的铁球熔化成一个球,则这个大球的半径应为
A 4 B C D
10、线和平面,能得出的一个条件是
A B
C D
11、线a、b和平面,下面推论错误的是
A. B
C D
12、设m、n是两条不同的直线,是三个不同的平面,给出下列四个命题:
①若,,则 ②若,,,则
③若,,则 ④若,,则
其中正确命题的序号是
A ①和② B ②和③ C ③和④ D ①和④
二、填空题(每小题4分,共16分)
13、已知圆锥的表面积为6,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为_______________.
14、用一张圆弧长等于12分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于 ______________立方分米.
15、设是外一点,则使点在此三角形所在平面内的射影是的垂心的条件为________________________(填一种即可).
16、已知直线是直线,是平面,给出下列命题:[来源:21世纪教育网]
① ,则;
② ,则;
③ ,则;
④ ,则.
其中正确命题的序号
选择题答题卡
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
三、解答题(共74分)
17、(本题12分)正四棱台的高是8cm,两底面的边长分别为4cm和16cm,求这个棱台的侧棱的长、斜高、表面积、体积.
18、(本题12分)三棱锥V—ABC中,VO⊥平面ABC, O∈CD , VA=VB,AD=BD.
证明:CD⊥AB且AC=BC .
19、(本题12分)如图,ABCD是正方形,O是正方形的中心,PO底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE ;
(2)平面PAC平面BDE.21世纪教育网
第19题 第20题
20、(本题12分)如图,在正方体中,为中点,
于。求证:⊥平面.21世纪教育网
21、(本题12分)如图,长方体中,,,点为的中点。
(1)求证:直线∥平面;
(2)求证:平面平面;
(3)求证:直线平面.
第21题
22、(本题14分)已知正方形所在平面与正方形所在平面互相垂直,M为上一点,N为 上一点,且有,设
(1) 求证:;
(2) 求证: ;
(3) 当为何值时,取最小值?并求出这个最小值.
参考答案
1-12题 ACBBB DDACC DA; 13、;14、96;15、 ; 16、①③④
17、解:如图:连结两底面中心,并连结和,
过作于,则为高,[来源:21世纪教育网]
为斜高,
在中,cm,
在中,cm,
cm
cm
棱台的侧棱长为cm,斜高为10 cm,表面积为672 cm,体积为896 cm
18、证:
19、证明(1)∵O是AC的中点,E是PC的中点,∴OE∥AP,
又∵OE平面BDE,PA平面BDE,∴PA∥平面BDE
(2)∵PO底面ABCD,∴POBD,又∵ACBD,且ACPO=O
∴BD平面PAC,而BD平面BDE,∴平面PAC平面BDE。
20、略
21、解:(1)设AC和BD交于点O,连PO,
由P,O分别是,BD的中点,故PO//,
所以直线∥平面--(4分)
(2)长方体中,,
底面ABCD是正方形,则ACBD
又面ABCD,则AC,
所以AC面,则平面平面
(3)PC2=2,PB12=3,B1C2=5,所以△PB1C是直角三角形。PC,
同理PA,所以直线平面。--(14分)
22、证明:(1) 在平面ABC中,作,在平面BFE中,作,连结GH
MNHG为平行四边形;
又GH面BEC,MN面BEC
MN//面BEC
(2)
AB面BEC
GH面GEC ABGH
MN//GH MNAB21世纪教育网
(3) 面ABCD面ABEF
BE面ABCD BEBC
BG= , BH=
MN=GH==
=()
= 当且仅当时,等号成立;
当时,MN取最小值.
