(新人教b版必修2)数学:1.2.1《平面的基本性质及推论》课件
文档属性
| 名称 | (新人教b版必修2)数学:1.2.1《平面的基本性质及推论》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 109.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-09 00:00:00 | ||
图片预览



文档简介
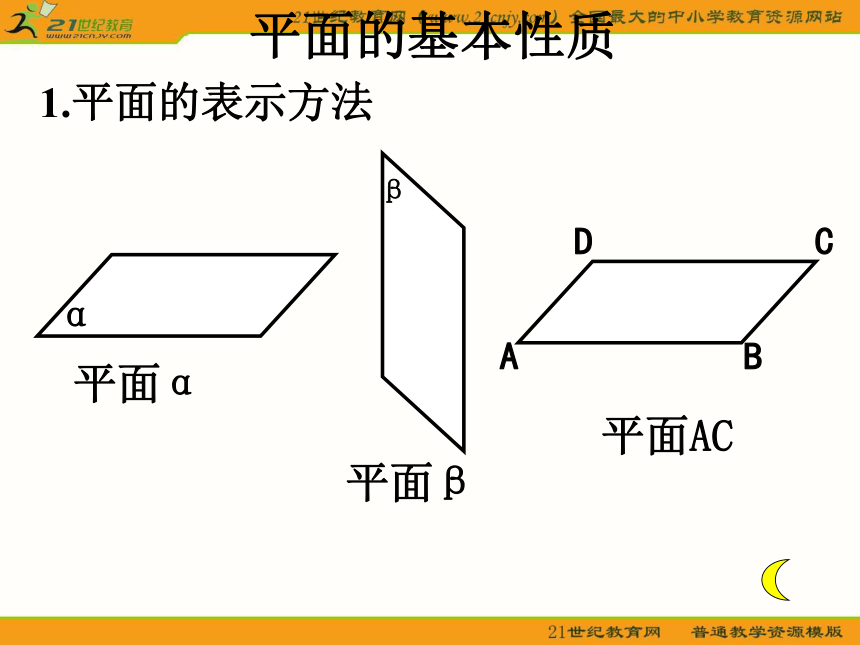
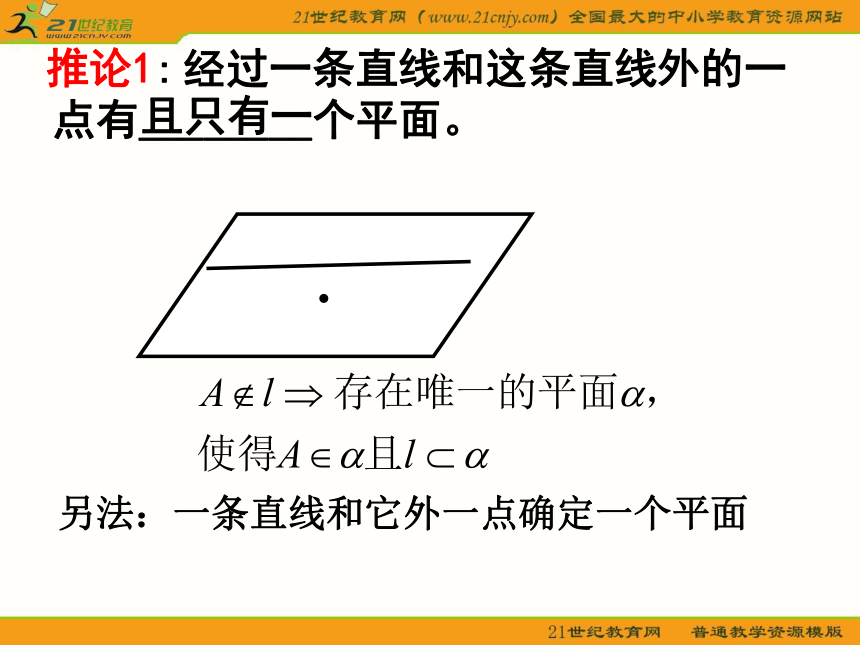
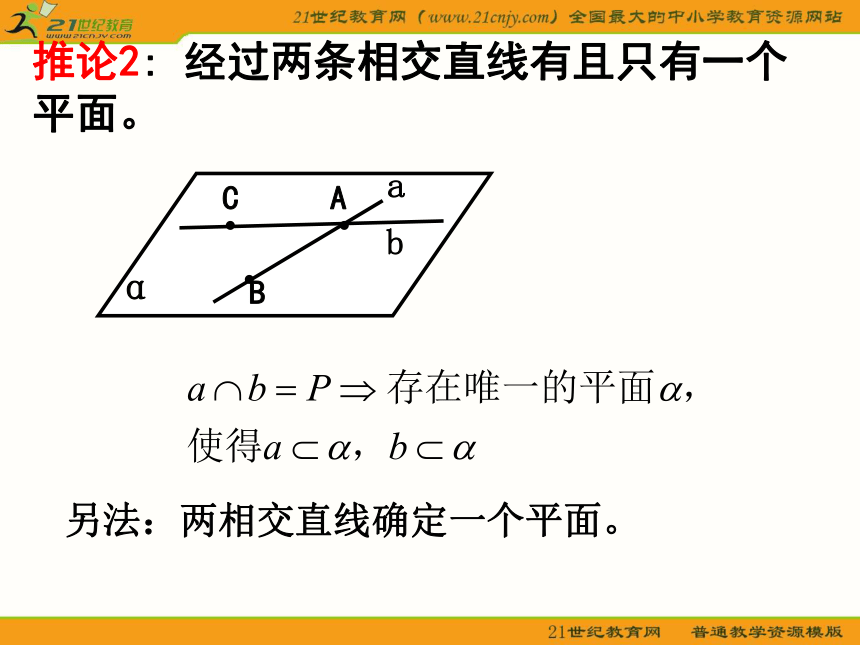
课件19张PPT。1.平面的表示方法平面的基本性质 2.平面的基本性质公理1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。公理3 :如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是一条直线。 公理2:经过不在同一条直线上的三点有且只有一个平面。(即不共线的三点确定一平面)1.平面的表示方法平面的基本性质 推论1: 经过一条直线和这条直线外的一点有________个平面。且只有一另法:一条直线和它外一点确定一个平面AA推论2: 经过两条相交直线有且只有一个 平面。ABC另法:两相交直线确定一个平面。已知:直线a、b且a∩b=P.
求证:过a、b有且只有一个平面。证明:PAC(1)存在性
在直线a上取不同于点P的点A
则点A 直线b.
根据推论1,过点A和直线b有一个平面α。
(2)唯一性。
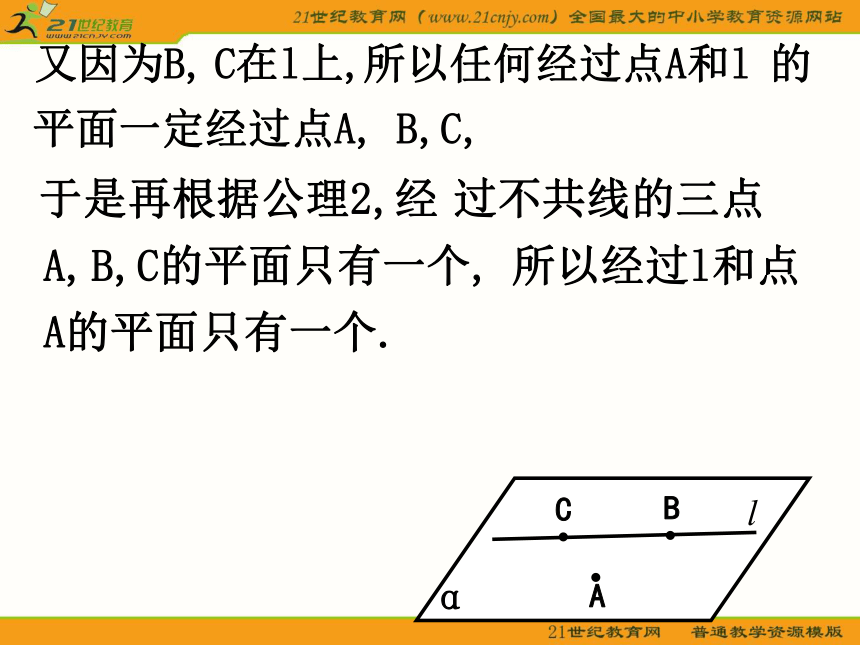
∵经过直线a、b的平面一定经过点A和直线b,
而A b。
根据推论1,经过点A和直线b的平面只有一个.
∴经过a、b的平面只有一个.由(1)(2),可知经过两条相交直线
有且只有一个平面。 推论3:经过两条平行直线有且只有一个平面。C另法:两条平行直线确定一个平面。已知:直线a、b且a∥b.
求证:经过直线a、b有且只有一个平面.B证明:(1)存在性.
∵a∥b,由平行线的定义,
a、b在同一平面内,
∴过直线a、b有一个平面α.
(2)唯一性。在直线b上任取一点B,则B a(否则与a∥b 矛盾)
且B、a在过a、b的平面α内。
又由推论1,过点B和直线a的平面只有一个,
∴过直线a、b的平面只有一个。
由(1)(2),可知经过两条平行直线的平面
有且只有一个。(1)如果空间几个点或几条直线都在同一平面内,那么我们就说它们共面.(2)如果构成图形的所有点都在同一平面内,这个图形叫做平面图形.(3)如果构成图形的点不都在同一平面内,这种图形叫做立体图形.(4)我们在初中学过的平面图形的某些性质,例如全等、平行、相似等,对空间里的平面图形仍然成立。注:公理1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。公理3:如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是一条直线。 公理2:经过不在同一条直线上的三点有且只有一个平面。(即不共线的三点确定一平面)推论1:经过一条直线和这条直线外的一点有且只有一个平面。推论2: 经过两条相交直线有且只有一个 平面。 推论3:经过两条平行直线有且只有一个平面。平面的基本性质公理1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。公理3:如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是一条直线。 公理2:经过不在同一条直线上的三点有且只有一个平面。推论1:经过一条直线和这条直线外的一点有且只有一个平面。推论2: 经过两条相交直线有且只有一个平面。 推论3:经过两条平行直线有且只有一个平面。基本题型证明线共点:先确定两条直线交点,再证交点在第三条直线上。证明点共线:证明这些点同时在两相交平面内证明点共面或线共面:先由一些元素确定一个平面,再证另一些元素也在这个平面内。已知:直线a∥b∥c,a∩l=A,b∩l=B,c∩l=C
求证:a,b,c,l共面aA证明:又∵a∩l=A,b∩l=B, ∵a∥b∴a,b,c,l共面bcBClABCDMOBCDAGHEFM
求证:过a、b有且只有一个平面。证明:PAC(1)存在性
在直线a上取不同于点P的点A
则点A 直线b.
根据推论1,过点A和直线b有一个平面α。
(2)唯一性。
∵经过直线a、b的平面一定经过点A和直线b,
而A b。
根据推论1,经过点A和直线b的平面只有一个.
∴经过a、b的平面只有一个.由(1)(2),可知经过两条相交直线
有且只有一个平面。 推论3:经过两条平行直线有且只有一个平面。C另法:两条平行直线确定一个平面。已知:直线a、b且a∥b.
求证:经过直线a、b有且只有一个平面.B证明:(1)存在性.
∵a∥b,由平行线的定义,
a、b在同一平面内,
∴过直线a、b有一个平面α.
(2)唯一性。在直线b上任取一点B,则B a(否则与a∥b 矛盾)
且B、a在过a、b的平面α内。
又由推论1,过点B和直线a的平面只有一个,
∴过直线a、b的平面只有一个。
由(1)(2),可知经过两条平行直线的平面
有且只有一个。(1)如果空间几个点或几条直线都在同一平面内,那么我们就说它们共面.(2)如果构成图形的所有点都在同一平面内,这个图形叫做平面图形.(3)如果构成图形的点不都在同一平面内,这种图形叫做立体图形.(4)我们在初中学过的平面图形的某些性质,例如全等、平行、相似等,对空间里的平面图形仍然成立。注:公理1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。公理3:如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是一条直线。 公理2:经过不在同一条直线上的三点有且只有一个平面。(即不共线的三点确定一平面)推论1:经过一条直线和这条直线外的一点有且只有一个平面。推论2: 经过两条相交直线有且只有一个 平面。 推论3:经过两条平行直线有且只有一个平面。平面的基本性质公理1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。公理3:如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是一条直线。 公理2:经过不在同一条直线上的三点有且只有一个平面。推论1:经过一条直线和这条直线外的一点有且只有一个平面。推论2: 经过两条相交直线有且只有一个平面。 推论3:经过两条平行直线有且只有一个平面。基本题型证明线共点:先确定两条直线交点,再证交点在第三条直线上。证明点共线:证明这些点同时在两相交平面内证明点共面或线共面:先由一些元素确定一个平面,再证另一些元素也在这个平面内。已知:直线a∥b∥c,a∩l=A,b∩l=B,c∩l=C
求证:a,b,c,l共面aA证明:又∵a∩l=A,b∩l=B, ∵a∥b∴a,b,c,l共面bcBClABCDMOBCDAGHEFM
