(苏教版必修2)数学:2.2.2直线与圆的位置关系
文档属性
| 名称 | (苏教版必修2)数学:2.2.2直线与圆的位置关系 |

|
|
| 格式 | rar | ||
| 文件大小 | 108.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-10 00:00:00 | ||
图片预览







文档简介
课件23张PPT。《直线与圆的位置关系》为了大家能看的更清楚些.
以蓝线为水平线,圆圈为太阳!
注意观察!!请大家把直线和圆的公共点个数情况
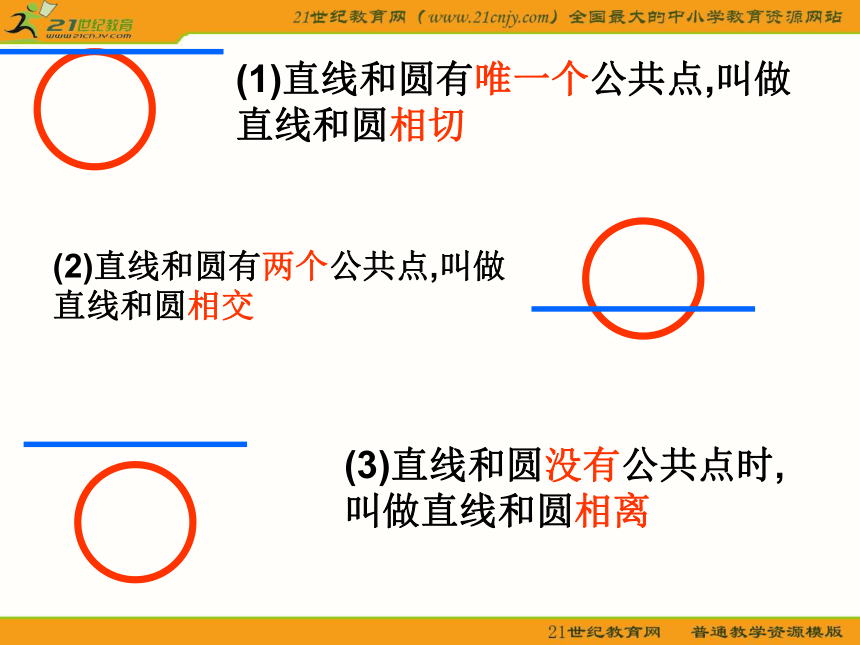
总结一下,并把相应的图形画出来.总体看来应该有下列三种情况:(1)直线和圆有一个公共点(2)直线和圆有两个公共点.(3)直线和圆没有公共点.(1)直线和圆有唯一个公共点,叫做
直线和圆相切(2)直线和圆有两个公共点,叫做
直线和圆相交(3)直线和圆没有公共点时,
叫做直线和圆相离填表大家都知道:点和圆的位置关系可以用圆心到点之间的距离,这一数量关系来刻画他们的位置关系;那么直线和圆的位置关系是否也可以用数量关系来刻画他们三种位置关系呢?下面我们一起来研究一下!
o圆心O到直线L的距离dL半径r(1)直线L和⊙O的相离,此时d与r大小关系为_________d>ro半径r(2)直线L和⊙O相切,此时d与r大小关系为_________d=ro半径r(3)直线L和⊙O相交,此时d与r大小关系为_________dr时,能否得出直线和圆的位置关系为相离.
(2)当d=r时,能否得出直线和圆的位置关系为相切.
(3)当d (d为圆心O到直线L的距离,r为圆O的半径)思考:直线和圆的位置关系:直线L和⊙O相交 d直线L和⊙o相切 d=r
直线L和⊙o相离 d>r注明:符号” “读作”等价于”.它表示从左端可以推出右端,并且从右端也可以推出左端.设直线l和圆C的方程分别为:Ax+By+C=0,X2+y2+Dx+Ey+F=0由方程组的解确定直线与圆的位置关系如果直线l与圆C有公共点,由于公共点同时在l和C上,
所以公共点的坐标一定是这两个
方程的公共解;反之,如果这两个方程有公共解,
那么以公共解为坐标的点必是l与C的公共点.由直线l和圆C的方程联立方程组Ax+By+C=0X2+y2+Dx+Ey+F=0有如下结论:例1求直线4x+3y=40和圆x2+y2=100的公共点坐标,
并判断它们的位置关系.解这个方程组得解:例2:在Rt△ABC,∠C=900,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2 cm ; (2)r=2.4 cm ; (3) r=3 cm.例2:Rt△ABC,∠C=900,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2 cm ; (2)r=2.4 cm ; (3) r=3 cm.(1)当r在什么条件下,直线AB和圆C相交。(2)以B为圆心,以BC为半径画圆,
此时⊙B与AC间的位置关系。思考:例3自点A(-1,4)作圆(x-2)2+(y-3)2=1的切线l,
求切线l的方程.解法1:利用点到直线的距离公式解法2:联立成方程组,应用判别式求解.思考:过A点与圆相切的直线个数?2.在△ABC中,∠C=90,AC=3,AB=5,若以C为圆心、r为半径作圆,那么:
(1)当直线AB与⊙C相切时,r的取值范围是_________;
(2)当直线AB与⊙C相离时,r的取值范围是___________;
(3)当直线AB与⊙C相交时,r的取值范围是___________.
课堂练习1.课本105页练习1.2.3.?
210交点切点dr割线切线课堂小结直线和圆的位置关系主要有三种:相离、相切、相交.
(设⊙o半径为r,圆心到直线L的距离为d,那么:
以蓝线为水平线,圆圈为太阳!
注意观察!!请大家把直线和圆的公共点个数情况
总结一下,并把相应的图形画出来.总体看来应该有下列三种情况:(1)直线和圆有一个公共点(2)直线和圆有两个公共点.(3)直线和圆没有公共点.(1)直线和圆有唯一个公共点,叫做
直线和圆相切(2)直线和圆有两个公共点,叫做
直线和圆相交(3)直线和圆没有公共点时,
叫做直线和圆相离填表大家都知道:点和圆的位置关系可以用圆心到点之间的距离,这一数量关系来刻画他们的位置关系;那么直线和圆的位置关系是否也可以用数量关系来刻画他们三种位置关系呢?下面我们一起来研究一下!
o圆心O到直线L的距离dL半径r(1)直线L和⊙O的相离,此时d与r大小关系为_________d>ro半径r(2)直线L和⊙O相切,此时d与r大小关系为_________d=ro半径r(3)直线L和⊙O相交,此时d与r大小关系为_________d
(2)当d=r时,能否得出直线和圆的位置关系为相切.
(3)当d
直线L和⊙o相离 d>r注明:符号” “读作”等价于”.它表示从左端可以推出右端,并且从右端也可以推出左端.设直线l和圆C的方程分别为:Ax+By+C=0,X2+y2+Dx+Ey+F=0由方程组的解确定直线与圆的位置关系如果直线l与圆C有公共点,由于公共点同时在l和C上,
所以公共点的坐标一定是这两个
方程的公共解;反之,如果这两个方程有公共解,
那么以公共解为坐标的点必是l与C的公共点.由直线l和圆C的方程联立方程组Ax+By+C=0X2+y2+Dx+Ey+F=0有如下结论:例1求直线4x+3y=40和圆x2+y2=100的公共点坐标,
并判断它们的位置关系.解这个方程组得解:例2:在Rt△ABC,∠C=900,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2 cm ; (2)r=2.4 cm ; (3) r=3 cm.例2:Rt△ABC,∠C=900,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2 cm ; (2)r=2.4 cm ; (3) r=3 cm.(1)当r在什么条件下,直线AB和圆C相交。(2)以B为圆心,以BC为半径画圆,
此时⊙B与AC间的位置关系。思考:例3自点A(-1,4)作圆(x-2)2+(y-3)2=1的切线l,
求切线l的方程.解法1:利用点到直线的距离公式解法2:联立成方程组,应用判别式求解.思考:过A点与圆相切的直线个数?2.在△ABC中,∠C=90,AC=3,AB=5,若以C为圆心、r为半径作圆,那么:
(1)当直线AB与⊙C相切时,r的取值范围是_________;
(2)当直线AB与⊙C相离时,r的取值范围是___________;
(3)当直线AB与⊙C相交时,r的取值范围是___________.
课堂练习1.课本105页练习1.2.3.?
210交点切点d
(设⊙o半径为r,圆心到直线L的距离为d,那么:
