一次函数图象的应用（二）

课件24张PPT。一次函数图象的应用（二）
平和广兆中学一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?(1)农民自带的零钱是多少?(2)试求降价前y与x之间的关系式(3)由表达式你能求出降价前每千克的
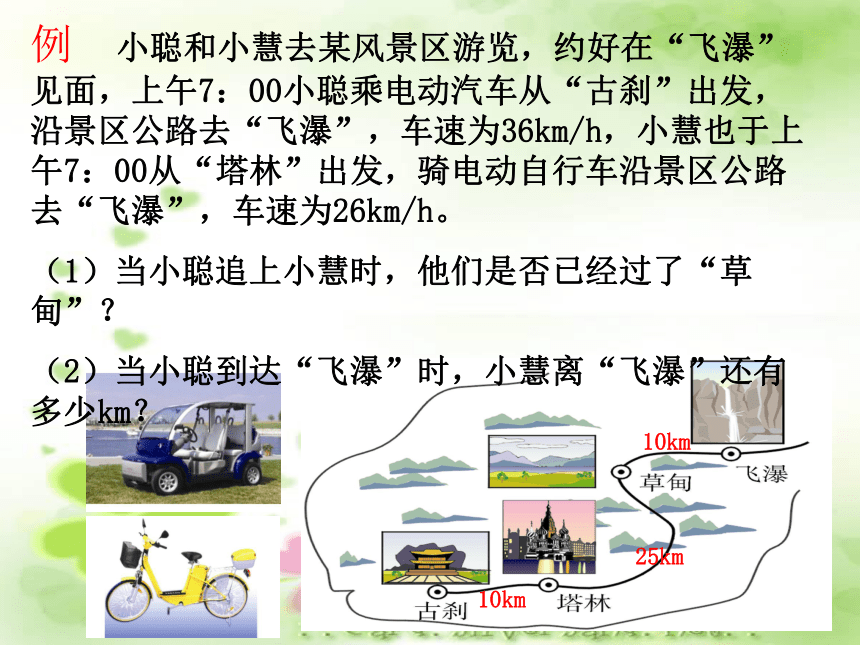
土豆价格是多少?例 小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？10km10km25km例 小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？分析：⑴两个人是否同时起步？ ⑷如果用S表示路程，t表示时间，那么他们的函数解析式是一样？他们各自的解析式分别是什么？小聪的解析式为小慧的解析式为S1=36tS2=26t+10⑶这个问题中的两个变量是什么？它们涉及的是什么函数关系？⑵在两个人到达之前所用时间是否相同？所行驶的路程是否相同？出发地点是否相同？两个人的速度各是多少？例 小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？当小聪追上小慧时，说明他们两个人的什么量是相同的？是否已经过了“草甸”该用什么量来表示？你会选择用哪种方式来解决？图象法？还是解析法？想一想：例 小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
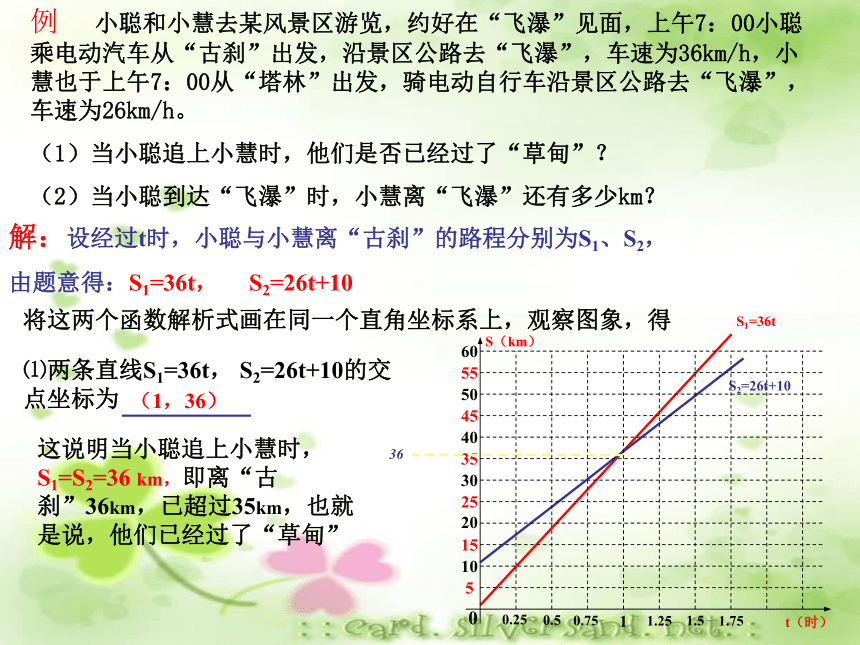
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？解：设经过t时，小聪与小慧离“古刹”的路程分别为S1、S2，
由题意得：S1=36t， S2=26t+10将这两个函数解析式画在同一个直角坐标系上，观察图象，得36S1=36tS2=26t+10⑴两条直线S1=36t， S2=26t+10的交点坐标为（1，36）这说明当小聪追上小慧时，S1=S2=36 km，即离“古刹”36km，已超过35km，也就是说，他们已经过了“草甸”例 小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
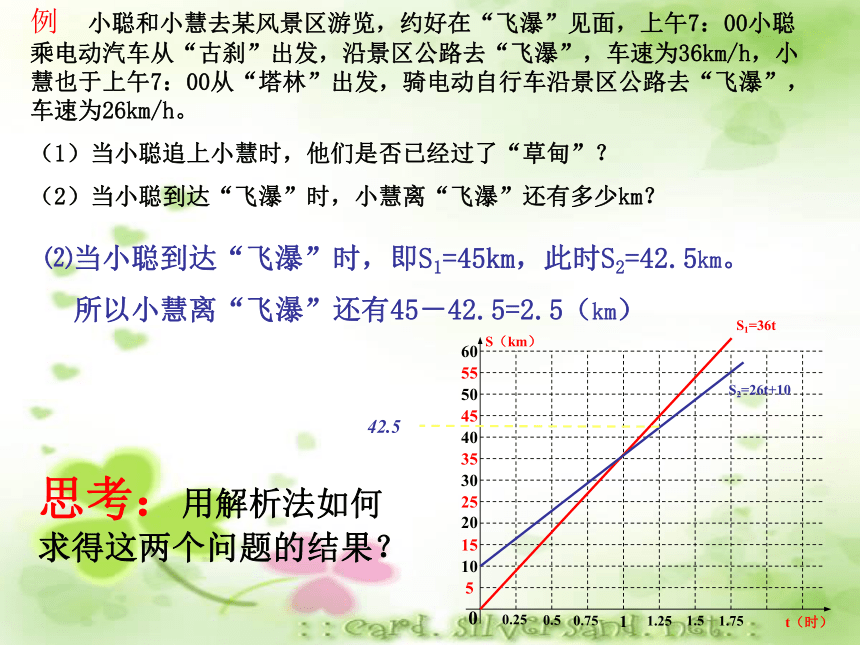
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？S1=36tS2=26t+1042.5⑵当小聪到达“飞瀑”时，即S1=45km，此时S2=42.5km。
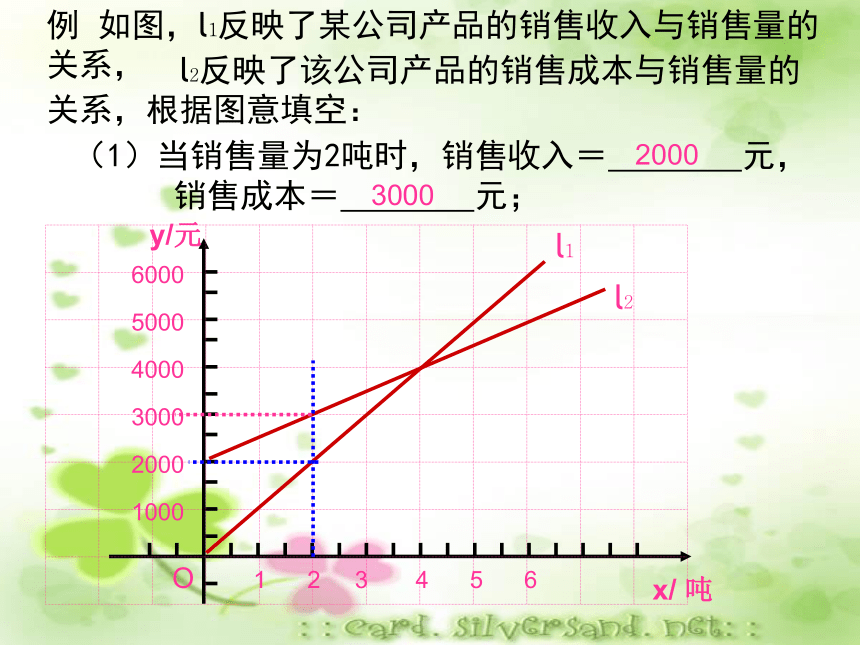
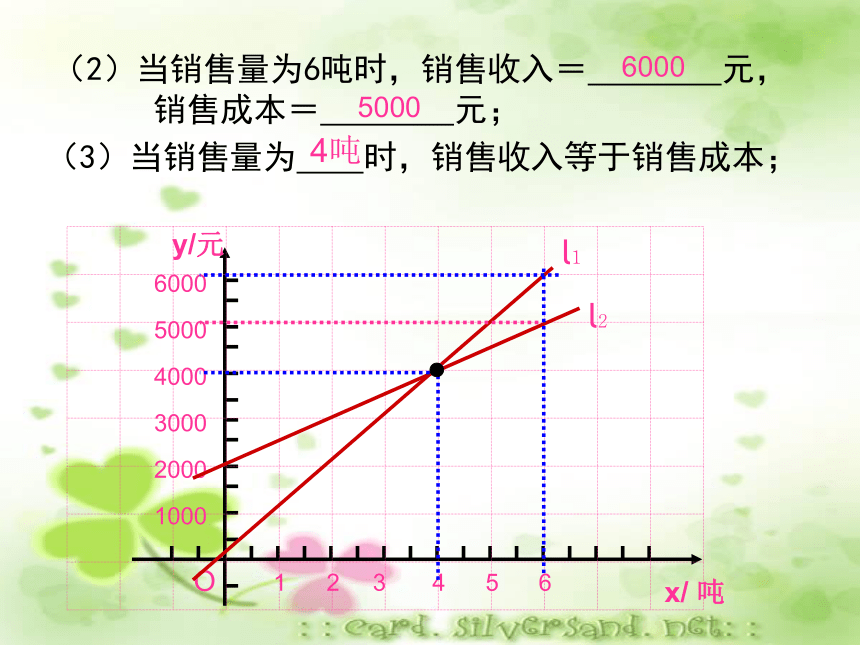
所以小慧离“飞瀑”还有45－42.5=2.5（km）思考：用解析法如何求得这两个问题的结果？例 如图，l1反映了某公司产品的销售收入与销售量的关系，（1）当销售量为2吨时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；2000l2l13000　　　　l2反映了该公司产品的销售成本与销售量的关系，根据图意填空：（2）当销售量为6吨时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；60005000（3）当销售量为　　时，销售收入等于销售成本；4吨（4）当销售量　　　　时，该公司赢利（收入大于成本）；
　　当销售量　　　　时，该公司亏损（收入小于成本）；大于4吨小于4吨（5） l1对应的函数表达式是　　　　　　　　，
　　 l2对应的函数表达式是　　　　　　　　。y=1000xy=500x+2000 例2　　我边防局接到情报，近海处有一可疑船只A正向公海方向行驶。边防局迅速派出快艇B追赶（如下图），海
岸公
海下图中l1 ，l2分别表示两船相对于海岸的距离s（海里）
与追赶时间t（分）之间的关系。根据图象回答下列问题：（1）哪条线表示B到海岸的距离与追赶时间之间的关系？解：观察图象，得当t＝0时，B距海岸0海里，即
　　　　　　　　　　　　　　　　S＝0，故l1表
　　　　　　　　　　　　　　　　示B到海岸的距
　　　　　　　　　　　　　　　　离与追赶时间之
　　　　　　　　　　　　　　　　间的关系；（2）A，B哪个速度快？从0增加到10时， l2的纵坐标增加了2，而l1的纵坐标增加了5，即10分内，A行驶了2海里，B行驶了5海里，所以B的速度快。（3）15分内B能否追上A？l1l2延长l1，l2，　　　　　可以看出，当t＝15时，l1上对应点在l2
上对应点的下方，这表明，15分时B尚未追上A。　　如图l1 ，l2相交于点P。（4）如果一直追下去，那么B能否追上A？l1l2因此，如果一直追下去，那么B一定能追上A。P（5）当A逃到离海岸12海里的公海时，B将无法对其进行检查。照此速度，B能否在A逃入公海前将其拦截？l1l2P　　从图中可以看出，l1与l1交点P的纵坐标小于12，　想一想你能用其他方法解决
上述问题吗？这说明在A逃入公海前，我边防快艇B能够追上A。5. 沙尘暴发生后，经过开阔荒漠时加速，经过乡镇、遇到防护林带区则减速，最终停止。某气象研究所观察一场沙尘暴从发生到结束的全过程，记录了风速y(km/h)随时间t（h）变化的图象（如图）
（1）??? 求沙尘暴的最大风速；
（2）????用恰当的方式表示沙尘暴风速y与时间t之间的关系。6. 如图，表示小王骑自行车和小李骑摩托车者沿相同的
路线由甲地到乙地行驶过程的函数图象，两地相距80千米，
请根据图象解决下列问题：
⑴⑷分别求出表示自行车和摩托车行驶过程的函数解析式，
并求出自变量x的取值范围．
复习、回顾：在运用一次函数解决实际问题时，首先判断问题中的两个变量之间是不是一次函数关系？当确定是一次函数关系时，可求出函数解析式，并运用一次函数的图象和性质进一步求得我们所需要的结果。谈本节课你有什么收获？作业：习题6.7