1.2.3相反数
图片预览








文档简介
课件21张PPT。第一章 有理数1.2.3 相 反 数1、画数轴,在数轴上表示出以下各点:
2,-3,2.5,-2.5,-2,3
2、观察所画的及数轴及表示的点回答下列问题:
(1)3与-3分别在原点的 和 。它们到原点的距离为: 。
(2)数轴上与原点距离是2 的点有 个,这些点表示的数是 。1、画数轴,在数轴上表示出以下各点:
2,-3,2.5,-2.5,-2,3
2、观察所画的及数轴及表示的点回答下列问题:
(1)3与-3分别在原点的 和 。它们到原点的距离为: 。
(2)数轴上与原点距离是2 的点有 个,这些点表示的数是 。
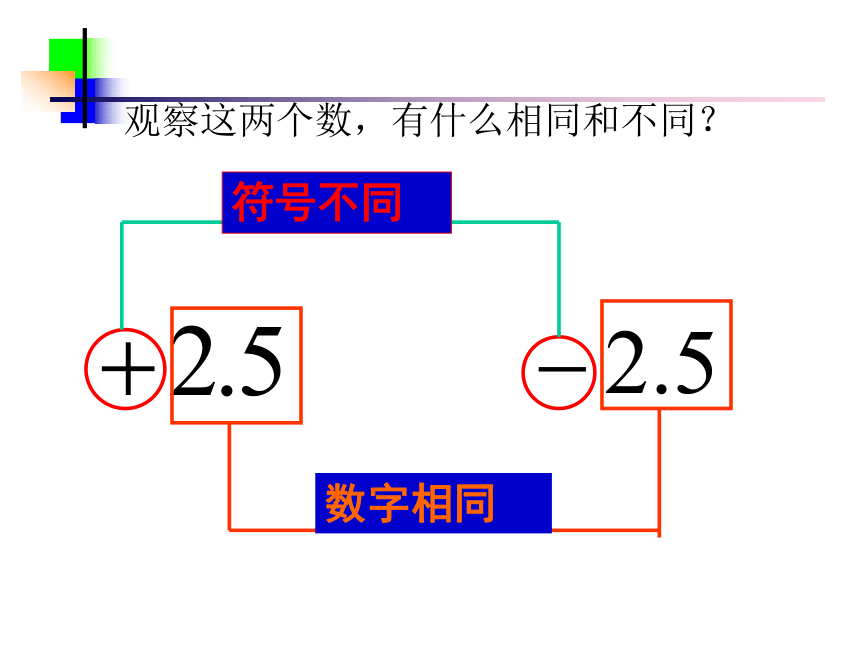
(3)数轴上与原点距离是5 的点有 个,这些点表示的数是 。一般地,设a是一个正数,数轴上与原点的距离是a 的点有 个,它们分别在原点的 ,表示 ,我们说这两点关于 。注意:到原点的距离相等。两左侧和右侧 -a和a原点对称观察这两个数,有什么相同和不同?数字相同符号不同像-2和2,3和-3,-2.5和2.5这样,只有符号不同的两个数叫做互为相反数。例如:8的相反数是-8,7的相反数是-7。
5的相反数是 .
由此可知,求一个数的相反数就是在这个数的
前面添上“-”号。一般地,a的相反数是 .-aa-a的相反数是 .a和-a互为相反数.如:???0的相反数是??(从数轴上考虑)0的相反数是0。一个正数的相反数是一个 。一个负数的相反数是一个 。负数正数一个数的相反数是它本身的数是:. 0想一想数轴上表示相反数的两个点和原点有什么关系? 在数轴上表示互为相反数的两个数的点,分别位于原点的两旁,且与原点的距离相等。 (二) 概念的理解
例2 判断:
(1)-2是-(-2)的相反数
(2)-3和+3都是相反数
(3)-3是3的相反数
(4)-3与+3互为相反数
(5)+3是-3的相反数
(6)一个数的相反数不可能是它本身例3 求下列各数的相反数:
(1)-5 (2) (3)0
(4) (5)-2b
(6) a-b (7) a+2
a 的相反数是-a , 求任意一个数的相反数就可以在这个数前加一个“-”号.
请说出下列各式表示的含义:
-(+1.1)表示什么呢?
-(-7)表示什么呢?,
-(-9.8)表示什么呢?
它们的结果应是多少?
典型例题例3 化简下列各数中的符号: (1)
(2)-(+5)
(3)
(4)今日作业例4 填空:
(1)a-4的相反数是 ,3-x的
相反数是 。
(2) 是 的相反数
(3)如果-a=-9,那么-a的相反数是 。 课堂小结例5 填空:
(1)若-(a-5)是负数,则a-5 0.
(2) 若是负数,则x+y 0.今日作业例6 已知a、b在数轴上的位置如图所示。
在数轴上作出它们的相反数;
用“<”按从小到大的顺序将这四个数连接起来。今日作业
2,-3,2.5,-2.5,-2,3
2、观察所画的及数轴及表示的点回答下列问题:
(1)3与-3分别在原点的 和 。它们到原点的距离为: 。
(2)数轴上与原点距离是2 的点有 个,这些点表示的数是 。1、画数轴,在数轴上表示出以下各点:
2,-3,2.5,-2.5,-2,3
2、观察所画的及数轴及表示的点回答下列问题:
(1)3与-3分别在原点的 和 。它们到原点的距离为: 。
(2)数轴上与原点距离是2 的点有 个,这些点表示的数是 。
(3)数轴上与原点距离是5 的点有 个,这些点表示的数是 。一般地,设a是一个正数,数轴上与原点的距离是a 的点有 个,它们分别在原点的 ,表示 ,我们说这两点关于 。注意:到原点的距离相等。两左侧和右侧 -a和a原点对称观察这两个数,有什么相同和不同?数字相同符号不同像-2和2,3和-3,-2.5和2.5这样,只有符号不同的两个数叫做互为相反数。例如:8的相反数是-8,7的相反数是-7。
5的相反数是 .
由此可知,求一个数的相反数就是在这个数的
前面添上“-”号。一般地,a的相反数是 .-aa-a的相反数是 .a和-a互为相反数.如:???0的相反数是??(从数轴上考虑)0的相反数是0。一个正数的相反数是一个 。一个负数的相反数是一个 。负数正数一个数的相反数是它本身的数是:. 0想一想数轴上表示相反数的两个点和原点有什么关系? 在数轴上表示互为相反数的两个数的点,分别位于原点的两旁,且与原点的距离相等。 (二) 概念的理解
例2 判断:
(1)-2是-(-2)的相反数
(2)-3和+3都是相反数
(3)-3是3的相反数
(4)-3与+3互为相反数
(5)+3是-3的相反数
(6)一个数的相反数不可能是它本身例3 求下列各数的相反数:
(1)-5 (2) (3)0
(4) (5)-2b
(6) a-b (7) a+2
a 的相反数是-a , 求任意一个数的相反数就可以在这个数前加一个“-”号.
请说出下列各式表示的含义:
-(+1.1)表示什么呢?
-(-7)表示什么呢?,
-(-9.8)表示什么呢?
它们的结果应是多少?
典型例题例3 化简下列各数中的符号: (1)
(2)-(+5)
(3)
(4)今日作业例4 填空:
(1)a-4的相反数是 ,3-x的
相反数是 。
(2) 是 的相反数
(3)如果-a=-9,那么-a的相反数是 。 课堂小结例5 填空:
(1)若-(a-5)是负数,则a-5 0.
(2) 若是负数,则x+y 0.今日作业例6 已知a、b在数轴上的位置如图所示。
在数轴上作出它们的相反数;
用“<”按从小到大的顺序将这四个数连接起来。今日作业
