第二十三章 旋转全章学案
文档属性
| 名称 | 第二十三章 旋转全章学案 |

|
|
| 格式 | rar | ||
| 文件大小 | 166.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-10 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
23.1 图形的旋转(1)
学习目标:
1.掌握旋转的概念,了解旋转中心、旋转角、旋转方向、对应点的概念及其应用。
2.掌握旋转的性质,应用概念解决一些实际问题.
重、难点:
1.对数学中的旋转现象做出分析.
2.对数学中的旋转现象的探索.
学习过程:
一、学习准备
1.请同学们看讲台上的大时钟,有什么在不停地转动?旋绕什么点呢?从现在到下课时钟转了多少度?分针转了多少度?秒针转了多少度?
2.看课本P56思考完成问题。并举一些现实中的例子。
二、探索新知
1.旋转的概念及旋转的三要素:
2.完成课本P56练习T1.2.3
3.看课本P57探究完成问题并指出旋转中心、旋转角、旋转方向、 各组对应点。
4.归纳旋转的性质。
三、巩固练习
1.在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________.
2. 如图,四边形ABCD是正方形,△DCE旋转后能与△DAF重合,那么旋转中心是 点.对应边是 ;对应角是 ;旋转角是 ;旋转角等于 度;连结EF后,△DEF是 三角形.
3.如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
四、拓展提高
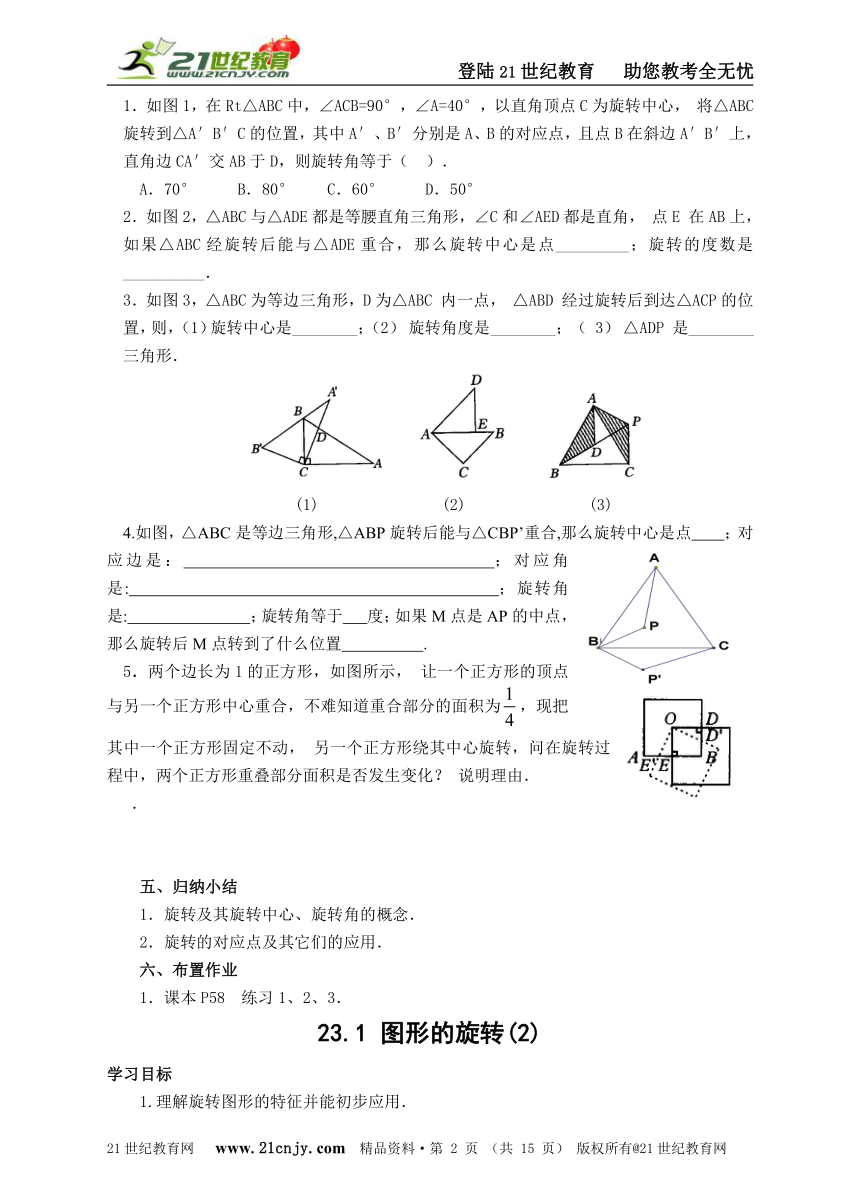
1.如图1,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( ).
A.70° B.80° C.60° D.50°
2.如图2,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是__________.
3.如图3,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是________;(2)旋转角度是________;(3)△ADP是________三角形.
( http: / / )
(1) (2) (3)
4.如图,△ABC是等边三角形,△ABP旋转后能与△CBP’重合,那么旋转中心是点 ;对应边是: ;对应角是: ;旋转角是: ;旋转角等于 度;如果M点是AP的中点,那么旋转后M点转到了什么位置 .
5.两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为,现把其中一个正方形固定不动,另一个正方形绕其中心旋转,问在旋转过程中,两个正方形重叠部分面积是否发生变化?说明理由.
.
五、归纳小结
1.旋转及其旋转中心、旋转角的概念.
2.旋转的对应点及其它们的应用.
六、布置作业
1.课本P58 练习1、2、3.
23.1 图形的旋转(2) ( http: / / )
学习目标
1.理解旋转图形的特征并能初步应用.
2.掌握图形旋转的基本作图。
重难点
1.图形的旋转的基本性质及其应用.
2.运用性质及基本作图.
学习过程
一、学前准备
1.什么叫旋转?什么叫旋转中心?什么叫旋转角?什么叫旋转的对应点?
2.我们怎样做出一个图形旋转后的图形?
3.各对应点到旋转中心的距离有何关系呢?各对应点与旋转中心所连线段的夹角与旋转角有何关系?两个图形是旋转前后的图形,它们全等吗?
二、运用新知
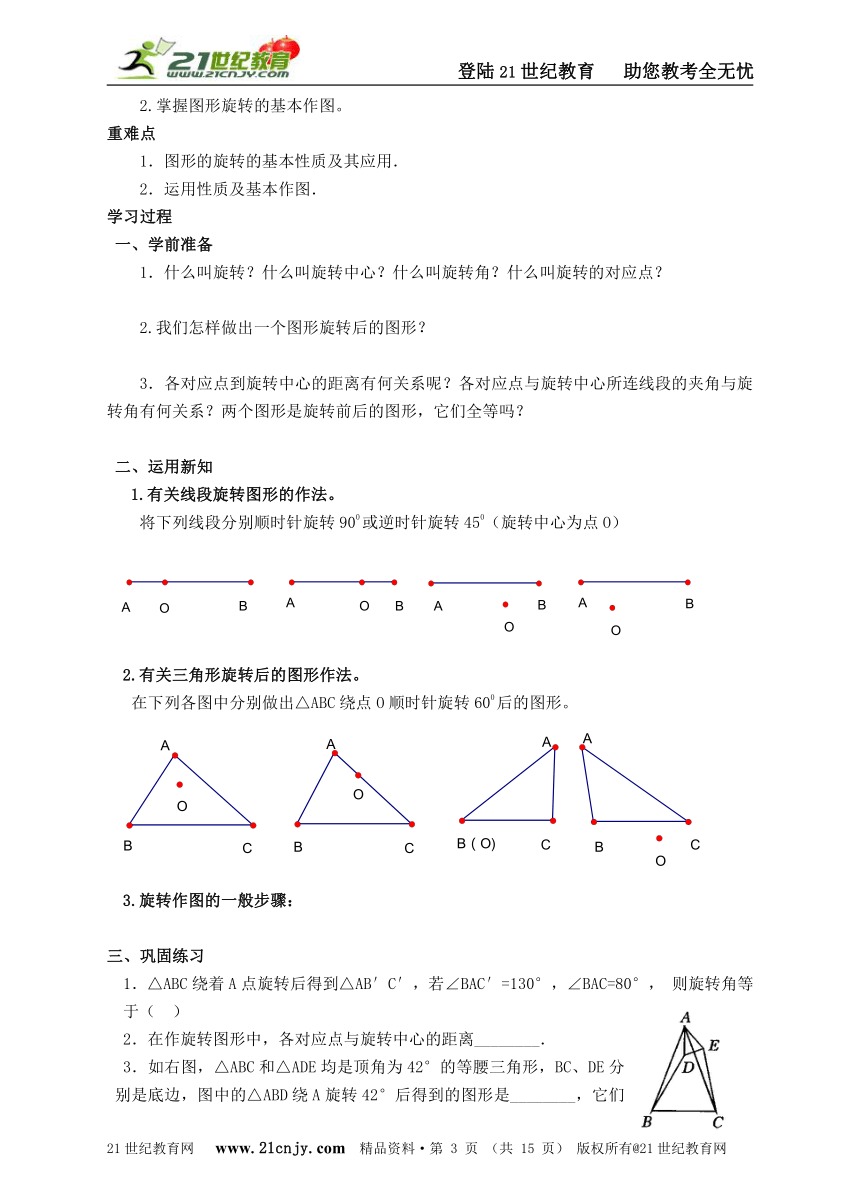
1.有关线段旋转图形的作法。
将下列线段分别顺时针旋转900或逆时针旋转450(旋转中心为点O)
2.有关三角形旋转后的图形作法。
在下列各图中分别做出△ABC绕点O顺时针旋转600后的图形。
3.旋转作图的一般步骤:
三、巩固练习
1.△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于( )
2.在作旋转图形中,各对应点与旋转中心的距离________.
3.如右图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是________,它们之间的关系是______,其中BD=_________.
4.如图,△ABC绕C点旋转后,顶点A的对应点为点D,
试确定顶点B对应点的位置,以及旋转后的三角形.
四、拓展提高
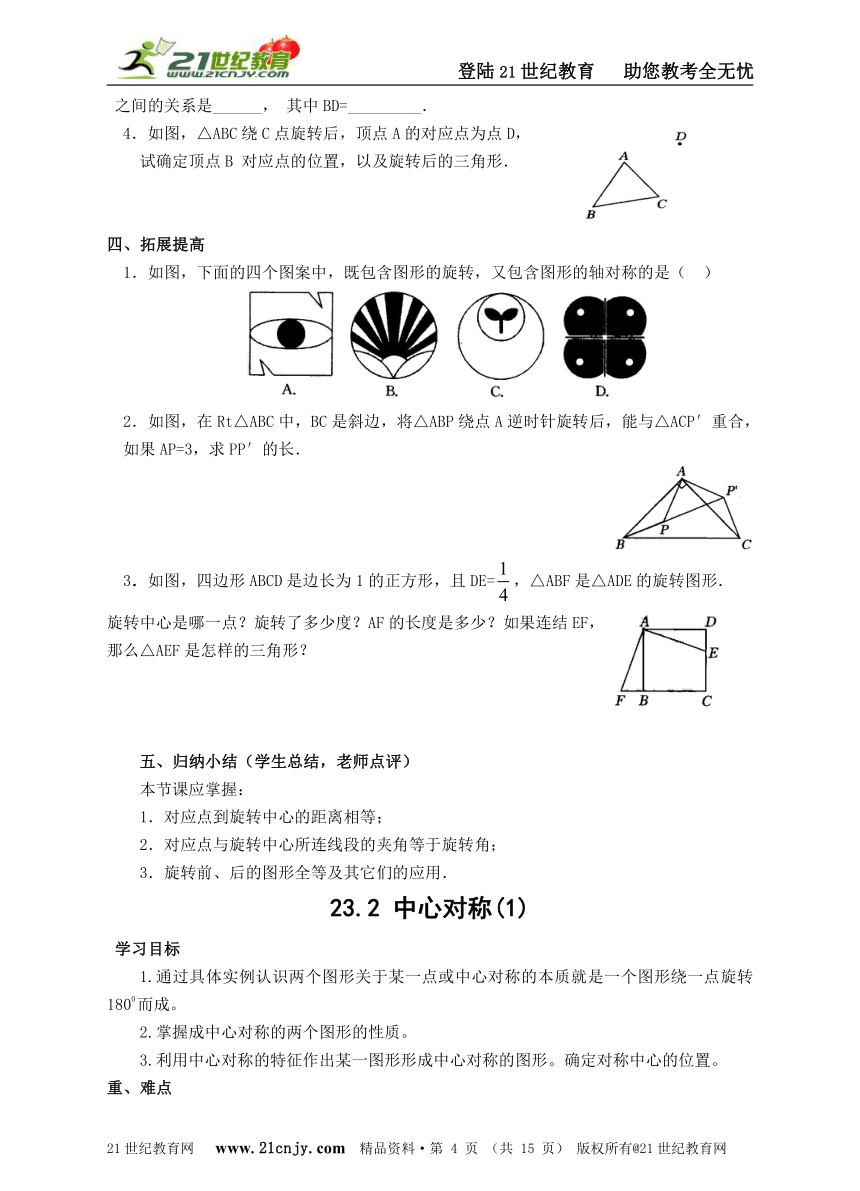
1.如图,下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是( )
( http: / / )
2.如图,在Rt△ABC中,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,求PP′的长.
3.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.
旋转中心是哪一点?旋转了多少度?AF的长度是多少?如果连结EF,那么△AEF是怎样的三角形?
五、归纳小结(学生总结,老师点评)
本节课应掌握:
1.对应点到旋转中心的距离相等;
2.对应点与旋转中心所连线段的夹角等于旋转角;
3.旋转前、后的图形全等及其它们的应用.
23.2 中心对称(1) ( http: / / )
学习目标
1.通过具体实例认识两个图形关于某一点或中心对称的本质就是一个图形绕一点旋转1800而成。
2.掌握成中心对称的两个图形的性质。
3.利用中心对称的特征作出某一图形形成中心对称的图形。确定对称中心的位置。
重、难点
利用中心对称、对称中心、关于中心对称点的概念解决一些问题.
学习过程
一、复习引入
1.回顾旋转的有关概念及性质。
2.如图,△ABC绕点O旋转,使点A旋转到点D处,画出旋转后的三角形,并写出简要作法.
3.请阅读课本P62思考及课本你有何收获,请写下来。
二、探索新知
1.如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答.
(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.
由上述活动归纳中心对称的性质:
三、巩固练习
1.关于某一点成中心对称的两个图形,对称点连线必通过_________.
2.把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形是_________图形.
3.如图,是由两个半圆组成的图形,已知点B是AC的中点,画出此图形关于点B成中心对称的图形.
4.如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABD成中心对称的三角形.
四、应用拓展
1.在英文字母VWXYZ中,是中心对称的英文字母的个数有( )个.
A.1 B.2 C.3 D.4
2.下面的图案中,是中心对称图形的个数有( )个
( http: / / )
A.1 B.2 C.3 D.4
3.作出线段AO关于O点的对称图形,如图所示.
4.作出三角形AOB关于O点的对称图形,如图所示.
5.画一个与已知四边形ABCD中心对称图形。(1)以顶点A为对称中心;(2)以BC边的中点为对称中心。
如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
五、归纳小结(学生归纳,老师点评)
本节课应掌握:
1.中心对称及对称中心的概念;
2.关于中心的对称点的概念及其运用.
23.2 中心对称(2) ( http: / / )
学习目标
1.理解关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;理解关于中心对称的两个图形是全等图形;掌握这两个性质的运用.
2.复习中心对称的基本概念(中心对称、对称中心,关于中心的对称点),总结中心对称的基本性质.
重难点
1.中心对称的两条基本性质及其运用.
2.让学生合作讨论,得出中心对称的两条基本性质.
学习过程
一、复习引入
1.什么叫中心对称?什么叫对称中心?
2.什么叫关于中心的对称点?
3.关于中心对称的两个图形,对称点所连线段都经过__________,而且被对称中心所________.关于中心对称的两个图形是_________图形.
4.线段既是轴对称图形又是中心对称图形,它的对称轴是_________,它的对称中心是__________.
二、探索新知
1.请同学们认真研读课本P63探究。
2.请同学们(1)作△ABC一顶点为对称中心的对称图形;(2)作关于一定点O为对称中心的对称图形.并分组讨论能得到什么结论.
二、巩固练习
1.下面图形中既是轴对称图形又是中心对称图形的是( )
A.直角 B.等边三角形 C.直角梯形 D.两条相交直线
2.将矩形ABCD沿AE折叠,得到如图的所示的图形,
已知∠CED′=60°,则∠AED的大小是( )
A.60° B.50° C.75° D.55°
3.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
4.如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).
5.中心对称与中心对称图形的区别与联系。
三、应用拓展
1.如图,等边△ABC内有一点O,试说明:OA+OB>OC.
2.分别画出与已知四边形ABCD成中心对称的四边形,使它们满足以下条件:
(1)以顶点A为对称中心,(2)以BC边的中点K为对称中心.
3.如图,已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.
4.如图,A、B、C是新建的三个居民小区,我们已经在到三个小区距离相等的地方修建了一所学校M,现计划修建居民小区D,其要求:(1)到学校的距离与其它小区到学校的距离相等;(2)控制人口密度,有利于生态环境建设,试写居民小区D的位置.
四、归纳小结
本节课应掌握中心对称的两条基本性质
23.2 中心对称(3)
学习目标
1.理解P与点P′点关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P′(-x,-y)的运用.
2.复习轴对称、旋转,尤其是中心对称,知识迁移到关于原点对称的点的坐标的关系及其运用.
重、难点
1.两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点P′(-x,-y)及其运用.
2.关于原点对称的点的坐标的性质及其运用它解决实际问题.
学习过程
一、复习引入
1.已知点A和直线L,如图,请画出点A关于L对称的点A′.
2.任意锐角△ABO绕点O旋转180°,画出旋转后的图形.
二、探索新知
1. 在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答这些坐标与已知点的坐标有什么关系? 关于原点作中心对称时,①它们的横坐标与横坐标绝对值什么关系?纵坐标与纵坐标的绝对值又有什么关系?②坐标与坐标之间符号又有什么特点?
三、巩固练习
1.如果点P(-3,1),那么点P(-3,1)关于原点的对称点P′的坐标是P′_______.
2.x轴上的点关于原点对称的点一定在 上。
3.若点A(1-2a,a-1)关于原点对称的点是第一象限内的点,则a的取值范围是 。
4.已知A(0,-1)、B(3,0)利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
5.已知△ABC,A(1,2),B(-1,3),C(-2,4)利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
四、应用拓展
1.点A(m,n)关于原点对称的点在第四象限则m 0,n 0。
2.点P(2,-3)关于x轴对称点的坐标是P1( , );关于y轴对称点的坐标是P2( , );关于原点对称点的坐标是P3( , )。
3.在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么关系,请说明理由.
4.直线AB与x轴、y轴分别相交于A、B两点,且A(0,3),B(3,0),现将直线AB绕点O顺时针旋转90°得到直线A1B1.
(1)在图中画出直线A1B1;
(2)求出过线段A1B1中点的反比例函数解析式;
(3)是否存在另一条与直线A1B1平行的直线y=kx+b(我们发现互相平行的两条直线斜率k相等)它与双曲线只有一个交点,若存在,求此直线的解析式;若不存在,请说明不存在的理由.
五、归纳小结
本节课应掌握:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y),关于原点的对称点P′(-x,-y),及其利用这些特点解决一些实际问题.
23.3 课题学习 图案设计
学习目标
1.利用平移、轴对称和旋转的这些图形变换中的一种或组合进行图案设计,设计出称心如意的图案.
2.通过复习平移、轴对称、旋转的知识,然后利用这些知识让学生开动脑筋,敝开胸怀大胆联想,设计出一幅幅美丽的图案.
重、难点
1.设计图案.
2.如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案.
学习过程
一、复习引入
1.如图,已知线段CD是线段AB平移后的图形,D是B点的对称点,作出线段AB,并回答,AB与CD有什么位置关系.
2.如图,已知线段CD,作出线段CD关于对称轴L的对称线段C′D′,并说明CD与对称线段C′D′之间有什么关系?
3.如图,已知线段CD,作出线段CD关于D点旋转90°的旋转后的图形,并说明这两条线段之间有什么关系?
二、探索新知
1.请用以上所讲的平移、轴对称、旋转等图形变换中的一种或组合完成下面的图案设计.
2.按下面的步骤,请每一位同学完成一个别致的图案.
(1)准备一张正三角形纸片(课前准备)(如图a)
(2)把纸片任意撕成两部分(如图b,如图c)
(3)将撕好的如图b沿正三角形的一边作轴对称,得到新的图形.
(4)并将(3)得到的图形以正三角形的一个顶点作为旋转中心旋转,得到如图(d)(如图c)保持不动)
(5)把如图(d)平移到如图(c)的右边,得到如图(e)
(6)对如图(e)进行适当的修饰,使得到一个别致美丽的如图(f)的图案.
三、巩固练习
1.在图所示的4个图案中既包含图形的旋转,还有图形轴对称是( )
2.将三角形绕直线L旋转一周,可以得到如图所示的立体图形的是( )
3.基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变。
4.图形在平移、旋转变化过程中,图形的 和 不变,只是 发生了改变。
5.全等变换方式有 , , 。
四、应用拓展
1.(学生活动)请利用线段、三角形、矩形、菱形、圆作为基本图形,绘制一幅反映你身边面貌的图案,并在班级里交流展示.
2.你知道平移、旋转、轴对称变换的基本特征吗?2.想一想这三种图形变换有什么共性?
五、归纳小结
本节课应掌握:
利用平移、轴对称和旋转的图形变换中的一种或组合设计图案.
第十三章 《旋转》复习与小结
一、知识结构
二、知识点拨
1.旋转的概念和有关知识
2.旋转有哪些性质?
3.中心对称的概念、对称中心、对称点
4.成中心对称的图形有什么特点?
5.中心对称图形的概念,我们学过的图形有哪些是中心对称图形倾泻下来?
6.在平面直角坐标系中,关于原点对称的点的坐标有什么特点?
三、综合应用
㈠、选择题
1.已知点的坐标为,为坐标原点,连结,将线段绕点按逆时针方向旋转得,则点的坐标为( )
A. B. C. D.
2.如图,如果正方形ABCD旋转后能与正方形CDEF重合,那么图形所在的平面内可作旋转中心的点共有( )
A.1 个 B.2 个 C.3 个 D.4个
3.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )
A.50° B.60° C.70° D.80°
4.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
A.55° B.45° C.40° D.35°
(第2题) (第3题) (第45题)
5.下列图形中,是中心对称的图形有( )
①正方形 ;②长方形 ;③等边三角形; ④线段; ⑤角; ⑥平行四边形。
A.5个 B.2个 C.3个 D.4个
6.若将图中的每个字母都看成独立的图案,则这七个图案中是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
7.如下所示的4组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
8. 平面直角坐标系内一点P(-2,3)关于原点对称的点的坐标是( )
A.(3,-2) B. (2,3) C.(-2,-3) D. (2,-3)
㈡、填空题
1.如图,△ABC中,∠BAC=90°,AB=AC, △ABC按逆时针方向旋转一个角度后,成为△ACD,则图中的____________是旋转中心,旋转角是___________。
(第1题) (第2题) (第3题)
2.如图,将△AOB绕点O逆时针旋转90o,得到△A/OB/.若点A的坐标为(,),则点A/的坐标为__________.
3.如图用等腰直角三角板画,并将三角板沿方向平移到如图所示的虚线处后绕点逆时针方向旋转,则三角板的斜边与射线的夹角为______.
4.图形在平移、旋转变换过程中,图形的 和 不变.
5.已知,则点P关于原点的对称点P1在第________象限。
6.点P(2,3)绕着原点逆时针方向旋转90o与点P/重合,则P/的坐标为 。
7.若点P(-2,a)与P'(2,b)关于原点对称,则a+b的值是_____________.
8.如图23—A—8,△ABC绕点A旋转后到达△ADE处,若∠BAC=120°,∠BAD=30°,则∠DAE=__________,∠CAE=__________。
9.如图11-1所示,P是等边△ABC内一点,△BMC是由△BPA旋转所得,则∠PBM=_____________.
㈢、解答题
1.如图,点是等边内一点,.将绕点按顺时针方向旋转得,连接.
(1)求证:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)探究:当为多少度时,是等腰三角形?
2.四边形ABCD为正方形,△ADE经旋转后与△ABF重合,试问:
(1)旋转中心为哪个点?
(2)旋转角是哪个角?度数是几度?
3.四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
4.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?
5.如图所示,△ABP是由△ACE绕A点旋转得到的,那么△ABP与△ACE是什么关系?若∠BAP=40°,∠B=30°,∠PAC=20°,求旋转角及∠CAE、∠E、∠BAE的度数。
6.如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
∠AOD=90°,求∠B的度数。
7.在正方形ABCD中,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10㎝,求GH的长。
8.如图四边形ABCD为长方形,△ABC旋转后能与△AEF重合
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)连结FC,则△AFC是什么三角形?
9.如图,P是正三角形ABC 内的一点,且PA=6,PB=8,PC=10。若将△PAC绕点A逆时针旋转后,得到△P/AB。
⑴求点P与点P′之间的距离;⑵∠APB的度数。
㈣、尝试反思
_
B
_
C
_
A
①
②
③
④
A
B
M
O
图23—A—8
A
B
C
D
O
A
B
C
D
E
F
A
B
D
C
G
H
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 6 页 (共 15 页) 版权所有@21世纪教育网
23.1 图形的旋转(1)
学习目标:
1.掌握旋转的概念,了解旋转中心、旋转角、旋转方向、对应点的概念及其应用。
2.掌握旋转的性质,应用概念解决一些实际问题.
重、难点:
1.对数学中的旋转现象做出分析.
2.对数学中的旋转现象的探索.
学习过程:
一、学习准备
1.请同学们看讲台上的大时钟,有什么在不停地转动?旋绕什么点呢?从现在到下课时钟转了多少度?分针转了多少度?秒针转了多少度?
2.看课本P56思考完成问题。并举一些现实中的例子。
二、探索新知
1.旋转的概念及旋转的三要素:
2.完成课本P56练习T1.2.3
3.看课本P57探究完成问题并指出旋转中心、旋转角、旋转方向、 各组对应点。
4.归纳旋转的性质。
三、巩固练习
1.在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________.
2. 如图,四边形ABCD是正方形,△DCE旋转后能与△DAF重合,那么旋转中心是 点.对应边是 ;对应角是 ;旋转角是 ;旋转角等于 度;连结EF后,△DEF是 三角形.
3.如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
四、拓展提高
1.如图1,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( ).
A.70° B.80° C.60° D.50°
2.如图2,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是__________.
3.如图3,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是________;(2)旋转角度是________;(3)△ADP是________三角形.
( http: / / )
(1) (2) (3)
4.如图,△ABC是等边三角形,△ABP旋转后能与△CBP’重合,那么旋转中心是点 ;对应边是: ;对应角是: ;旋转角是: ;旋转角等于 度;如果M点是AP的中点,那么旋转后M点转到了什么位置 .
5.两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为,现把其中一个正方形固定不动,另一个正方形绕其中心旋转,问在旋转过程中,两个正方形重叠部分面积是否发生变化?说明理由.
.
五、归纳小结
1.旋转及其旋转中心、旋转角的概念.
2.旋转的对应点及其它们的应用.
六、布置作业
1.课本P58 练习1、2、3.
23.1 图形的旋转(2) ( http: / / )
学习目标
1.理解旋转图形的特征并能初步应用.
2.掌握图形旋转的基本作图。
重难点
1.图形的旋转的基本性质及其应用.
2.运用性质及基本作图.
学习过程
一、学前准备
1.什么叫旋转?什么叫旋转中心?什么叫旋转角?什么叫旋转的对应点?
2.我们怎样做出一个图形旋转后的图形?
3.各对应点到旋转中心的距离有何关系呢?各对应点与旋转中心所连线段的夹角与旋转角有何关系?两个图形是旋转前后的图形,它们全等吗?
二、运用新知
1.有关线段旋转图形的作法。
将下列线段分别顺时针旋转900或逆时针旋转450(旋转中心为点O)
2.有关三角形旋转后的图形作法。
在下列各图中分别做出△ABC绕点O顺时针旋转600后的图形。
3.旋转作图的一般步骤:
三、巩固练习
1.△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于( )
2.在作旋转图形中,各对应点与旋转中心的距离________.
3.如右图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是________,它们之间的关系是______,其中BD=_________.
4.如图,△ABC绕C点旋转后,顶点A的对应点为点D,
试确定顶点B对应点的位置,以及旋转后的三角形.
四、拓展提高
1.如图,下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是( )
( http: / / )
2.如图,在Rt△ABC中,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,求PP′的长.
3.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.
旋转中心是哪一点?旋转了多少度?AF的长度是多少?如果连结EF,那么△AEF是怎样的三角形?
五、归纳小结(学生总结,老师点评)
本节课应掌握:
1.对应点到旋转中心的距离相等;
2.对应点与旋转中心所连线段的夹角等于旋转角;
3.旋转前、后的图形全等及其它们的应用.
23.2 中心对称(1) ( http: / / )
学习目标
1.通过具体实例认识两个图形关于某一点或中心对称的本质就是一个图形绕一点旋转1800而成。
2.掌握成中心对称的两个图形的性质。
3.利用中心对称的特征作出某一图形形成中心对称的图形。确定对称中心的位置。
重、难点
利用中心对称、对称中心、关于中心对称点的概念解决一些问题.
学习过程
一、复习引入
1.回顾旋转的有关概念及性质。
2.如图,△ABC绕点O旋转,使点A旋转到点D处,画出旋转后的三角形,并写出简要作法.
3.请阅读课本P62思考及课本你有何收获,请写下来。
二、探索新知
1.如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答.
(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.
由上述活动归纳中心对称的性质:
三、巩固练习
1.关于某一点成中心对称的两个图形,对称点连线必通过_________.
2.把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形是_________图形.
3.如图,是由两个半圆组成的图形,已知点B是AC的中点,画出此图形关于点B成中心对称的图形.
4.如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABD成中心对称的三角形.
四、应用拓展
1.在英文字母VWXYZ中,是中心对称的英文字母的个数有( )个.
A.1 B.2 C.3 D.4
2.下面的图案中,是中心对称图形的个数有( )个
( http: / / )
A.1 B.2 C.3 D.4
3.作出线段AO关于O点的对称图形,如图所示.
4.作出三角形AOB关于O点的对称图形,如图所示.
5.画一个与已知四边形ABCD中心对称图形。(1)以顶点A为对称中心;(2)以BC边的中点为对称中心。
如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
五、归纳小结(学生归纳,老师点评)
本节课应掌握:
1.中心对称及对称中心的概念;
2.关于中心的对称点的概念及其运用.
23.2 中心对称(2) ( http: / / )
学习目标
1.理解关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;理解关于中心对称的两个图形是全等图形;掌握这两个性质的运用.
2.复习中心对称的基本概念(中心对称、对称中心,关于中心的对称点),总结中心对称的基本性质.
重难点
1.中心对称的两条基本性质及其运用.
2.让学生合作讨论,得出中心对称的两条基本性质.
学习过程
一、复习引入
1.什么叫中心对称?什么叫对称中心?
2.什么叫关于中心的对称点?
3.关于中心对称的两个图形,对称点所连线段都经过__________,而且被对称中心所________.关于中心对称的两个图形是_________图形.
4.线段既是轴对称图形又是中心对称图形,它的对称轴是_________,它的对称中心是__________.
二、探索新知
1.请同学们认真研读课本P63探究。
2.请同学们(1)作△ABC一顶点为对称中心的对称图形;(2)作关于一定点O为对称中心的对称图形.并分组讨论能得到什么结论.
二、巩固练习
1.下面图形中既是轴对称图形又是中心对称图形的是( )
A.直角 B.等边三角形 C.直角梯形 D.两条相交直线
2.将矩形ABCD沿AE折叠,得到如图的所示的图形,
已知∠CED′=60°,则∠AED的大小是( )
A.60° B.50° C.75° D.55°
3.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
4.如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).
5.中心对称与中心对称图形的区别与联系。
三、应用拓展
1.如图,等边△ABC内有一点O,试说明:OA+OB>OC.
2.分别画出与已知四边形ABCD成中心对称的四边形,使它们满足以下条件:
(1)以顶点A为对称中心,(2)以BC边的中点K为对称中心.
3.如图,已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.
4.如图,A、B、C是新建的三个居民小区,我们已经在到三个小区距离相等的地方修建了一所学校M,现计划修建居民小区D,其要求:(1)到学校的距离与其它小区到学校的距离相等;(2)控制人口密度,有利于生态环境建设,试写居民小区D的位置.
四、归纳小结
本节课应掌握中心对称的两条基本性质
23.2 中心对称(3)
学习目标
1.理解P与点P′点关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P′(-x,-y)的运用.
2.复习轴对称、旋转,尤其是中心对称,知识迁移到关于原点对称的点的坐标的关系及其运用.
重、难点
1.两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点P′(-x,-y)及其运用.
2.关于原点对称的点的坐标的性质及其运用它解决实际问题.
学习过程
一、复习引入
1.已知点A和直线L,如图,请画出点A关于L对称的点A′.
2.任意锐角△ABO绕点O旋转180°,画出旋转后的图形.
二、探索新知
1. 在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答这些坐标与已知点的坐标有什么关系? 关于原点作中心对称时,①它们的横坐标与横坐标绝对值什么关系?纵坐标与纵坐标的绝对值又有什么关系?②坐标与坐标之间符号又有什么特点?
三、巩固练习
1.如果点P(-3,1),那么点P(-3,1)关于原点的对称点P′的坐标是P′_______.
2.x轴上的点关于原点对称的点一定在 上。
3.若点A(1-2a,a-1)关于原点对称的点是第一象限内的点,则a的取值范围是 。
4.已知A(0,-1)、B(3,0)利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
5.已知△ABC,A(1,2),B(-1,3),C(-2,4)利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
四、应用拓展
1.点A(m,n)关于原点对称的点在第四象限则m 0,n 0。
2.点P(2,-3)关于x轴对称点的坐标是P1( , );关于y轴对称点的坐标是P2( , );关于原点对称点的坐标是P3( , )。
3.在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么关系,请说明理由.
4.直线AB与x轴、y轴分别相交于A、B两点,且A(0,3),B(3,0),现将直线AB绕点O顺时针旋转90°得到直线A1B1.
(1)在图中画出直线A1B1;
(2)求出过线段A1B1中点的反比例函数解析式;
(3)是否存在另一条与直线A1B1平行的直线y=kx+b(我们发现互相平行的两条直线斜率k相等)它与双曲线只有一个交点,若存在,求此直线的解析式;若不存在,请说明不存在的理由.
五、归纳小结
本节课应掌握:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y),关于原点的对称点P′(-x,-y),及其利用这些特点解决一些实际问题.
23.3 课题学习 图案设计
学习目标
1.利用平移、轴对称和旋转的这些图形变换中的一种或组合进行图案设计,设计出称心如意的图案.
2.通过复习平移、轴对称、旋转的知识,然后利用这些知识让学生开动脑筋,敝开胸怀大胆联想,设计出一幅幅美丽的图案.
重、难点
1.设计图案.
2.如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案.
学习过程
一、复习引入
1.如图,已知线段CD是线段AB平移后的图形,D是B点的对称点,作出线段AB,并回答,AB与CD有什么位置关系.
2.如图,已知线段CD,作出线段CD关于对称轴L的对称线段C′D′,并说明CD与对称线段C′D′之间有什么关系?
3.如图,已知线段CD,作出线段CD关于D点旋转90°的旋转后的图形,并说明这两条线段之间有什么关系?
二、探索新知
1.请用以上所讲的平移、轴对称、旋转等图形变换中的一种或组合完成下面的图案设计.
2.按下面的步骤,请每一位同学完成一个别致的图案.
(1)准备一张正三角形纸片(课前准备)(如图a)
(2)把纸片任意撕成两部分(如图b,如图c)
(3)将撕好的如图b沿正三角形的一边作轴对称,得到新的图形.
(4)并将(3)得到的图形以正三角形的一个顶点作为旋转中心旋转,得到如图(d)(如图c)保持不动)
(5)把如图(d)平移到如图(c)的右边,得到如图(e)
(6)对如图(e)进行适当的修饰,使得到一个别致美丽的如图(f)的图案.
三、巩固练习
1.在图所示的4个图案中既包含图形的旋转,还有图形轴对称是( )
2.将三角形绕直线L旋转一周,可以得到如图所示的立体图形的是( )
3.基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变。
4.图形在平移、旋转变化过程中,图形的 和 不变,只是 发生了改变。
5.全等变换方式有 , , 。
四、应用拓展
1.(学生活动)请利用线段、三角形、矩形、菱形、圆作为基本图形,绘制一幅反映你身边面貌的图案,并在班级里交流展示.
2.你知道平移、旋转、轴对称变换的基本特征吗?2.想一想这三种图形变换有什么共性?
五、归纳小结
本节课应掌握:
利用平移、轴对称和旋转的图形变换中的一种或组合设计图案.
第十三章 《旋转》复习与小结
一、知识结构
二、知识点拨
1.旋转的概念和有关知识
2.旋转有哪些性质?
3.中心对称的概念、对称中心、对称点
4.成中心对称的图形有什么特点?
5.中心对称图形的概念,我们学过的图形有哪些是中心对称图形倾泻下来?
6.在平面直角坐标系中,关于原点对称的点的坐标有什么特点?
三、综合应用
㈠、选择题
1.已知点的坐标为,为坐标原点,连结,将线段绕点按逆时针方向旋转得,则点的坐标为( )
A. B. C. D.
2.如图,如果正方形ABCD旋转后能与正方形CDEF重合,那么图形所在的平面内可作旋转中心的点共有( )
A.1 个 B.2 个 C.3 个 D.4个
3.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )
A.50° B.60° C.70° D.80°
4.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
A.55° B.45° C.40° D.35°
(第2题) (第3题) (第45题)
5.下列图形中,是中心对称的图形有( )
①正方形 ;②长方形 ;③等边三角形; ④线段; ⑤角; ⑥平行四边形。
A.5个 B.2个 C.3个 D.4个
6.若将图中的每个字母都看成独立的图案,则这七个图案中是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
7.如下所示的4组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
8. 平面直角坐标系内一点P(-2,3)关于原点对称的点的坐标是( )
A.(3,-2) B. (2,3) C.(-2,-3) D. (2,-3)
㈡、填空题
1.如图,△ABC中,∠BAC=90°,AB=AC, △ABC按逆时针方向旋转一个角度后,成为△ACD,则图中的____________是旋转中心,旋转角是___________。
(第1题) (第2题) (第3题)
2.如图,将△AOB绕点O逆时针旋转90o,得到△A/OB/.若点A的坐标为(,),则点A/的坐标为__________.
3.如图用等腰直角三角板画,并将三角板沿方向平移到如图所示的虚线处后绕点逆时针方向旋转,则三角板的斜边与射线的夹角为______.
4.图形在平移、旋转变换过程中,图形的 和 不变.
5.已知,则点P关于原点的对称点P1在第________象限。
6.点P(2,3)绕着原点逆时针方向旋转90o与点P/重合,则P/的坐标为 。
7.若点P(-2,a)与P'(2,b)关于原点对称,则a+b的值是_____________.
8.如图23—A—8,△ABC绕点A旋转后到达△ADE处,若∠BAC=120°,∠BAD=30°,则∠DAE=__________,∠CAE=__________。
9.如图11-1所示,P是等边△ABC内一点,△BMC是由△BPA旋转所得,则∠PBM=_____________.
㈢、解答题
1.如图,点是等边内一点,.将绕点按顺时针方向旋转得,连接.
(1)求证:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)探究:当为多少度时,是等腰三角形?
2.四边形ABCD为正方形,△ADE经旋转后与△ABF重合,试问:
(1)旋转中心为哪个点?
(2)旋转角是哪个角?度数是几度?
3.四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
4.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?
5.如图所示,△ABP是由△ACE绕A点旋转得到的,那么△ABP与△ACE是什么关系?若∠BAP=40°,∠B=30°,∠PAC=20°,求旋转角及∠CAE、∠E、∠BAE的度数。
6.如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
∠AOD=90°,求∠B的度数。
7.在正方形ABCD中,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10㎝,求GH的长。
8.如图四边形ABCD为长方形,△ABC旋转后能与△AEF重合
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)连结FC,则△AFC是什么三角形?
9.如图,P是正三角形ABC 内的一点,且PA=6,PB=8,PC=10。若将△PAC绕点A逆时针旋转后,得到△P/AB。
⑴求点P与点P′之间的距离;⑵∠APB的度数。
㈣、尝试反思
_
B
_
C
_
A
①
②
③
④
A
B
M
O
图23—A—8
A
B
C
D
O
A
B
C
D
E
F
A
B
D
C
G
H
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 6 页 (共 15 页) 版权所有@21世纪教育网
同课章节目录
