分类计数原理与分步计数原理
图片预览







文档简介
课件20张PPT。分类计数原理
与
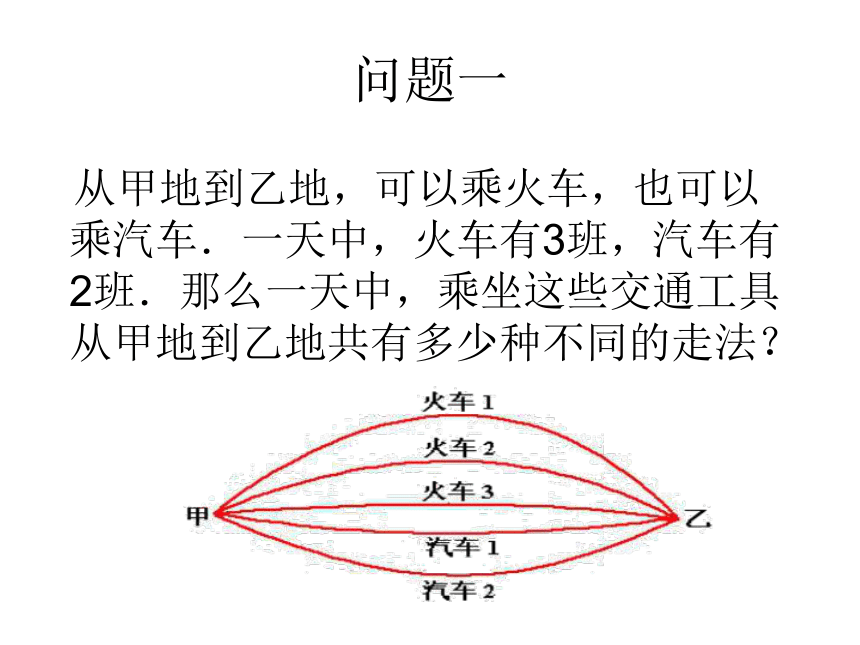
分步计数原理问题一 从甲地到乙地,可以乘火车,也可以乘汽车.一天中,火车有3班,汽车有2班.那么一天中,乘坐这些交通工具从甲地到乙地共有多少种不同的走法?分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法。那么完成这件事共有
N=m+n
种不同的方法分类计数原理完成一件事,有n类办法,在第1类办法中有 种不同的方法,在第2类办法中有 种不同的方法……在第n类办法中有 种不同的方法.那么完成这件事共有
N= 种不同的方法(加法原理)关于分类计数原理的几点注记: ⑴各类办法之间相互独立,都能完成这件事,且办法
总数是各类办法相加,所以这个原理又叫做加法原
理; ⑵分类时,首先要在问题的条件之下确定一个分类标
准,然后在确定的分类标准下进行分类; ⑶完成这件事的任何一种方法必属于某一类,且分别
属于不同两类的两种方法都是不同的——不重不漏. 例1 在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各自有一些自己感兴趣的强项专业,具体如下:A大学
生物学
化学
医学
物理学
工程学B大学
数学
会计学
信息技术学
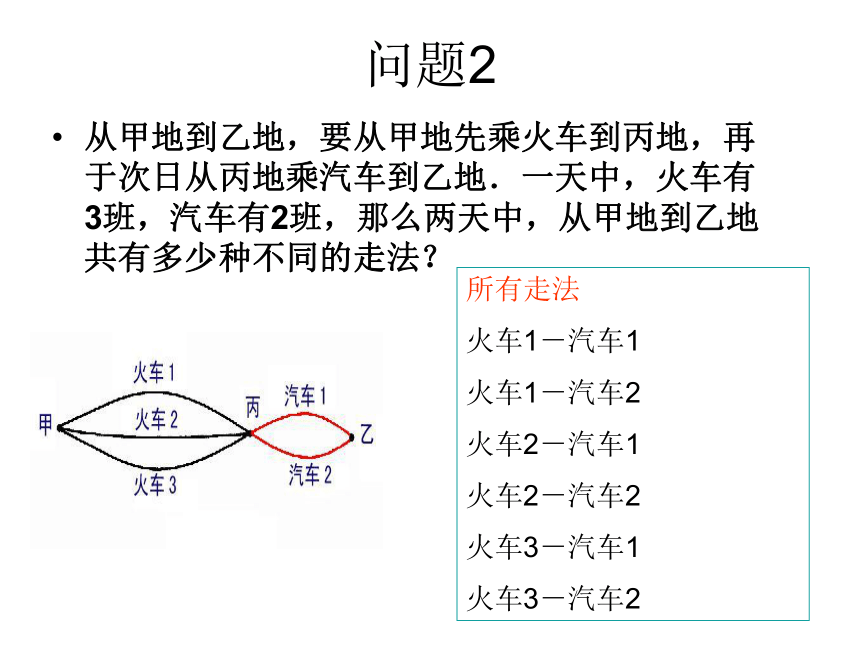
法学那么,这名同学可能的专业选择共有多少种?解:在A大学中有5种专业选择,在B大学中有4种专业选择方法。由于没有一个专业是两所大学共有,因此根据分类加法计数原理,这名同学可能选择的专业共有5+4=9(种)问题2从甲地到乙地,要从甲地先乘火车到丙地,再于次日从丙地乘汽车到乙地.一天中,火车有3班,汽车有2班,那么两天中,从甲地到乙地共有多少种不同的走法?所有走法
火车1-汽车1
火车1-汽车2
火车2-汽车1
火车2-汽车2
火车3-汽车1
火车3-汽车2分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有
N=m×n
种不同的方法分步计数原理完成一件事,需要分成n个步骤,做第1步有 种不同的方法,做第2步有 种不同的方法……做第n步有 种不同的方法.那么完成这件事共有
N= 种不同的方法.(乘法原理)关于分步计数原理的几点注记⑴各个步骤之间相互依存,且方法总数是各个步骤
的方法数相乘,所以这个原理又叫做乘法原理 ;⑵分步时首先要在问题的条件之下确定一个分步标
准,然后在确定的分步标准下分步; ⑶完成这件事的任何一种方法必须并且只需连续完
成每一个步骤. 例2 设某班有男生30名,女生24名,现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?分析:选出一组参赛代表,可以分两个步骤。第一步选男生,第二步选女生。解:第一步,从30名男生中选出1人,有30种不同选择;第二步,从24名女生中选出1人,有24种不同选择根据分步乘法计数原理,共有 30×24=720
种不同的选法。答:共有720种选法。分类计数原理与分步计数原理的区别区别在于:
1.分类计数原理针对的是“分类”问题,其中各种方法相互独立,用中任何一种方法都可以做完这件事;
2.分步计数原理针对的是“分步”问题,各个步骤中的方法相互依存,只有各个步骤都完成才算做完这件事.例3 书架的第一层放有4本不同的计算机书,第二层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取一本书,有几种不同的取法?解:⑴从书架上任取一本书,有3类办法:
第1类办法是从第1层取1本计算机书,有4种方法;
第2类办法是从第2层取1本文艺书,有3种方法;
第3类办法是从第3层取一本体育书,有2种方法.
根据分类计数原理,不同取法的种数是
N=4+3+2=9.
答:从书架上任取1本书,有9种不同的取法. 例3 书架的第一层放有4本不同的计算机书,第二层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取一本书,有几种不同的取法?解: (2)从书架的第1,2,3层各取1本书,可以分成3个步骤完成: 根据分步乘法计数原理,不同取法的种数是
N=4×3×2=24.
答:从书架的第1,2,3层各取1本书,有24种不同的取法. 第3个步骤是从第3层取一本体育书,有2种方法.第2个步骤是从第2层取1本文艺书,有3种方法;第1个步骤是从第1层取1本计算机书,有4种方法;例4 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左右两边墙上的指定位置,问共有多少种不同的挂法?解:从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:第二步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法。根据分布乘法计数原理,不同挂法的种数是
N=3×2=6第一步,从3幅画中选出1幅挂在左边墙上,有3种选法;答:共有6种不同的挂法。 要从甲、乙、丙3名工人中选出2名分别上日班和晚班,有多少种不同的选法?6种选法可以表示如下:
日班 晚班
甲 乙
甲 丙
乙 甲
乙 丙
丙 甲
丙 乙变式:已知直线Ax+By+1=0,若A,B从-5,-3,-1,0,2,4,7这7个数中选取不同的两个数,求斜率小于0的直线有______条.从0,1,2,3,5,7,11中任取3个元素分别作为直线方程Ax+By+C=0中的系数A,B,C,所得经过坐标原点的直线有_______条。 一种号码锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成多少个四位数字号码?解:由于号码锁的每个拨号盘有从0到9这10个数字,每个拨号盘上的数字有10种取法.
根据分步计数原理,4个拨号盘上各取1个数字组成四位数字号码的个数是
N=10×10×10×10=10000.
答:可以组成10000个四位数字号码. 4张卡片的正、反面分别0与1,2与3,4与5,6与7,将其中3张卡片排放在一起,可以组成多少个不同的三位数?1.(1)4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有多少种报名方法?(2)4名同学争夺跑步、跳高、跳远三项冠军(假设冠军只有一人),共有多少种可能的结果2.有4部车床,需加工3个不同的零件,其不同的安排方法有多少种?3.设集合A={1,2,3,4},B={5,6,7},则从A到B的所有不同映射的个数是:
A.81 B.64 C.12 D.274.集合M={1,2,3,4}的子集个数是:
A.6 B.8 C.12 D.16
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法。那么完成这件事共有
N=m+n
种不同的方法分类计数原理完成一件事,有n类办法,在第1类办法中有 种不同的方法,在第2类办法中有 种不同的方法……在第n类办法中有 种不同的方法.那么完成这件事共有
N= 种不同的方法(加法原理)关于分类计数原理的几点注记: ⑴各类办法之间相互独立,都能完成这件事,且办法
总数是各类办法相加,所以这个原理又叫做加法原
理; ⑵分类时,首先要在问题的条件之下确定一个分类标
准,然后在确定的分类标准下进行分类; ⑶完成这件事的任何一种方法必属于某一类,且分别
属于不同两类的两种方法都是不同的——不重不漏. 例1 在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各自有一些自己感兴趣的强项专业,具体如下:A大学
生物学
化学
医学
物理学
工程学B大学
数学
会计学
信息技术学
法学那么,这名同学可能的专业选择共有多少种?解:在A大学中有5种专业选择,在B大学中有4种专业选择方法。由于没有一个专业是两所大学共有,因此根据分类加法计数原理,这名同学可能选择的专业共有5+4=9(种)问题2从甲地到乙地,要从甲地先乘火车到丙地,再于次日从丙地乘汽车到乙地.一天中,火车有3班,汽车有2班,那么两天中,从甲地到乙地共有多少种不同的走法?所有走法
火车1-汽车1
火车1-汽车2
火车2-汽车1
火车2-汽车2
火车3-汽车1
火车3-汽车2分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有
N=m×n
种不同的方法分步计数原理完成一件事,需要分成n个步骤,做第1步有 种不同的方法,做第2步有 种不同的方法……做第n步有 种不同的方法.那么完成这件事共有
N= 种不同的方法.(乘法原理)关于分步计数原理的几点注记⑴各个步骤之间相互依存,且方法总数是各个步骤
的方法数相乘,所以这个原理又叫做乘法原理 ;⑵分步时首先要在问题的条件之下确定一个分步标
准,然后在确定的分步标准下分步; ⑶完成这件事的任何一种方法必须并且只需连续完
成每一个步骤. 例2 设某班有男生30名,女生24名,现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?分析:选出一组参赛代表,可以分两个步骤。第一步选男生,第二步选女生。解:第一步,从30名男生中选出1人,有30种不同选择;第二步,从24名女生中选出1人,有24种不同选择根据分步乘法计数原理,共有 30×24=720
种不同的选法。答:共有720种选法。分类计数原理与分步计数原理的区别区别在于:
1.分类计数原理针对的是“分类”问题,其中各种方法相互独立,用中任何一种方法都可以做完这件事;
2.分步计数原理针对的是“分步”问题,各个步骤中的方法相互依存,只有各个步骤都完成才算做完这件事.例3 书架的第一层放有4本不同的计算机书,第二层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取一本书,有几种不同的取法?解:⑴从书架上任取一本书,有3类办法:
第1类办法是从第1层取1本计算机书,有4种方法;
第2类办法是从第2层取1本文艺书,有3种方法;
第3类办法是从第3层取一本体育书,有2种方法.
根据分类计数原理,不同取法的种数是
N=4+3+2=9.
答:从书架上任取1本书,有9种不同的取法. 例3 书架的第一层放有4本不同的计算机书,第二层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取一本书,有几种不同的取法?解: (2)从书架的第1,2,3层各取1本书,可以分成3个步骤完成: 根据分步乘法计数原理,不同取法的种数是
N=4×3×2=24.
答:从书架的第1,2,3层各取1本书,有24种不同的取法. 第3个步骤是从第3层取一本体育书,有2种方法.第2个步骤是从第2层取1本文艺书,有3种方法;第1个步骤是从第1层取1本计算机书,有4种方法;例4 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左右两边墙上的指定位置,问共有多少种不同的挂法?解:从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:第二步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法。根据分布乘法计数原理,不同挂法的种数是
N=3×2=6第一步,从3幅画中选出1幅挂在左边墙上,有3种选法;答:共有6种不同的挂法。 要从甲、乙、丙3名工人中选出2名分别上日班和晚班,有多少种不同的选法?6种选法可以表示如下:
日班 晚班
甲 乙
甲 丙
乙 甲
乙 丙
丙 甲
丙 乙变式:已知直线Ax+By+1=0,若A,B从-5,-3,-1,0,2,4,7这7个数中选取不同的两个数,求斜率小于0的直线有______条.从0,1,2,3,5,7,11中任取3个元素分别作为直线方程Ax+By+C=0中的系数A,B,C,所得经过坐标原点的直线有_______条。 一种号码锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成多少个四位数字号码?解:由于号码锁的每个拨号盘有从0到9这10个数字,每个拨号盘上的数字有10种取法.
根据分步计数原理,4个拨号盘上各取1个数字组成四位数字号码的个数是
N=10×10×10×10=10000.
答:可以组成10000个四位数字号码. 4张卡片的正、反面分别0与1,2与3,4与5,6与7,将其中3张卡片排放在一起,可以组成多少个不同的三位数?1.(1)4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有多少种报名方法?(2)4名同学争夺跑步、跳高、跳远三项冠军(假设冠军只有一人),共有多少种可能的结果2.有4部车床,需加工3个不同的零件,其不同的安排方法有多少种?3.设集合A={1,2,3,4},B={5,6,7},则从A到B的所有不同映射的个数是:
A.81 B.64 C.12 D.274.集合M={1,2,3,4}的子集个数是:
A.6 B.8 C.12 D.16
