(苏教版必修3)数学:2.2《总体分布的估计》测试
文档属性
| 名称 | (苏教版必修3)数学:2.2《总体分布的估计》测试 |

|
|
| 格式 | rar | ||
| 文件大小 | 75.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-14 00:00:00 | ||
图片预览



文档简介
高中苏教数学③2.2~2.3综合测试题
一、选择题
1.下列叙述中正确的是( )
A.从频率分布表可以看出样本数据对于平均数的波动大小
B.频数是指落在各个小组内的数据
C.每小组的频数与样本容量之比是这个小组的频率
D.组数是样本平均数除以组距
答案:C
2.如果五个数的平均数是7,那么这五个数的平均数是( )
A.5 B.6 C.7 D.8
答案:D
3.为了让人们感受到丢弃塑料袋对环境造成的影响,某班环保小组的六名同学记录了自己家中一周内丢弃的塑料袋的数量,结果如下(单位:个):33、25、28、26、25、31,如果该班有45名同学,那么根据提供的数据估计这周全班同学各家总共丢弃塑料袋的数量约为( )
A.900 B.1080 C.1260 D.1800
答案:C
4.一组数据的方差为3,将这组数据中的每一个数据都扩大到原来的3倍,则所得到的一组数据的方差是( )
A.1 B.27 C.9 D.3
答案:B
5.已知两个样本,甲:2,4,6,8,10;乙:1,3,5,7,9.样本方差分别为,则二者的关系是( )
A. B.
C. D.无法确定
答案:C
6.已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么下列样本范围的频率为0.25的是( ).
A.[5.5,7.5) B.[7.5,9.5)
C.[9.5,11.5) D.[11.5,13.5)
21世纪教育网
答案:D
二、填空题
7.一个容量为n的样本分成若干组,已知某组的频数和频率分别为30和0.25,则 .
答案:120
8.一个容量为20的样本数据,分组后,组距和频数如下:[10,20),2;[20,30),3;
[30,40),4;[40,50),5;[50,60),4;[60,70],2.则样本数据在区间[50,+∞)上的频率为 .
答案:0.3
9.五个数1,2,3,4,a的平均数是3,则这五个数的标准差是 .
答案:
10.某人射击十次,得环数如下:18,20,19,22,20,21,19,19,20,21,则这组数据的平均数是 ,方差是 .
答案:19.9,1.29
三、解答题
11.下表是60名学生的数学成绩的分组情况表:
分组
0.5~0.25
20.5~40.5[21世纪教育网
40.5~60.5
60.5~80.5
80.5~100.5
频数
3
6
12
频率
0.3
(1)在表中空格内填上相应数据;
(2)画出频率分布直方图.
解:(1)
分组
0.5~0.25
20.5~40.5
40.5~60.5
60.5~80.5
80.5~100.5
频数
3
6
12
21
18
频率
0.05
0.10
0.20
0.35
0.3
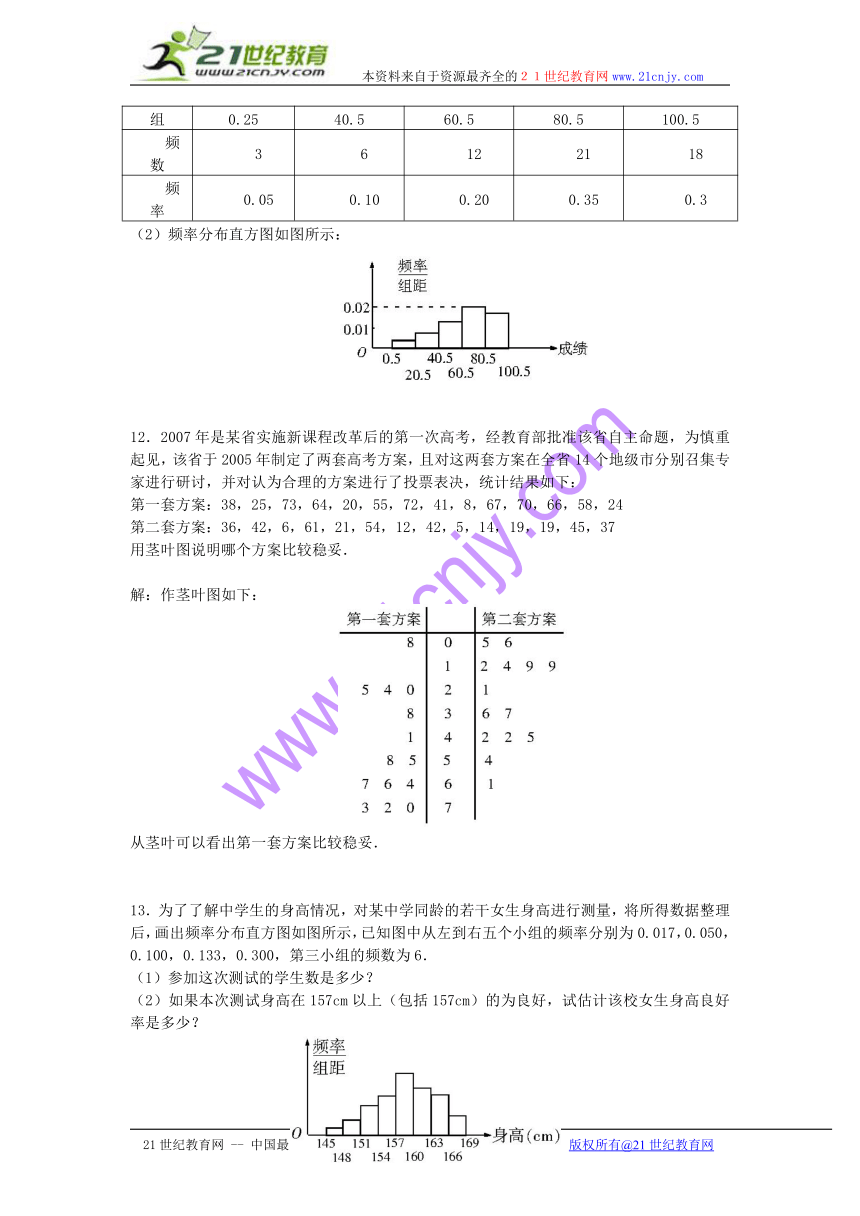
(2)频率分布直方图如图所示:
12.2007年是某省实施新课程改革后的第一次高考,经教育部批准该省自主命题,为慎重起见,该省于2005年制定了两套高考方案,且对这两套方案在全省14个地级市分别召集专家进行研讨,并对认为合理的方案进行了投票表决,统计结果如下:
第一套方案:38,25,73,64,20,55,72,41,8,67,70,66,58,24
第二套方案:36,42,6,61,21,54,12,42,5,14,19,19,45,37
用茎叶图说明哪个方案比较稳妥.
解:作茎叶图如下:
21世纪教育网
从茎叶可以看出第一套方案比较稳妥.
13.为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.
(1)参加这次测试的学生数是多少?
(2)如果本次测试身高在157cm以上(包括157cm)的为良好,试估计该校女生身高良好率是多少?
解:(1)由于,故参另这次测试的学生有60名;
(2)由于.
14.要从甲、乙、丙三位射击运动员中选拔一名参加比赛,在预选赛中,他们每人各打10发子弹,命中的环数如下:
甲:1010910999999
乙:1010109108810108
丙:1098108910999
根据这次成绩,应该派谁去参赛?
解:经计算,甲、乙、丙三人命中的总环数分别为93,93,91,所以应先淘汰丙.
设甲、乙平均成绩分别为,方差分别为,则,
,
,
虽然二者总成绩相同,但因为即,故甲的发挥比较稳定,所以应派甲去参赛.
高中苏教数学③2.2~2.3综合测试题
一、选择题
1.下列说法正确的是( ).
A.一组数据的标准差是这组数据的方差的平方
B.一组数据的平均数一定大于这组数据中的每个数据
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.一组数据的方差越大,说明这组数据的波动越大
答案:D
2.10名工人某天生产同一零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12.设其平均数为a,中位数为b,众数为c,则有( )
A. B.
C. D.
答案:D
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.3.5 B. C.3 D.
答案:B
4.两个样本,甲:5,4,3,2,1;乙:4,0,2,1,. 那么样本甲和样本乙的波动大小情况是( )
A.甲、乙波动大小一样
B.甲的波动比乙的波动大
C.乙的波动比甲的波动大21世纪教育网
D.甲、乙的波动大小无法比较
答案:C
二、填空题
5.频率分布扇形图是用圆中扇形面积与圆面积的比来表示各组成部分频率的统计图.现抽查20名学生的血型,结果如下:A,B,A,B,B,O,AB,A,A,O, A,B,A,A,B,AB,O,A,AB,A.则扇形图中表示B型血的扇形的圆心角的度数为 .
答案:
6.已知一个样本方差是,则这个样本的容量
是 ,平均数是 .
答案:10;4
7.已知样本99,100,101,的平均数是100,方差是2,则 .
答案:9996
8.已知样本80,82,84,86,88的方差为,且关于x的方程的两根的平方和恰好是,则 .
答案:
三、解答题
9.质检部门对甲、乙两种日光灯的使用时间进行了破坏性试验,10次试验得到的两种日光灯的使用时间如下两表所示,问:哪一种质量相对好一些?
使用时间(小时)
频数
2100
1
2110
2
212021世纪教育网
3
2130
3
2140
1
甲
使用时间(小时)
频数
2100
1
2110
1
2120
5
2130
2
2140
1
乙
解:(小时),
(小时)
又,
,
故,,
所以乙的质量好一些.
10.(1)计算下面几组数据的方差:
①1 2 3 4 5 6 7 8 9
②101 102 103 104 105 106 107 108 109
③401 402 403 404 405 406 407 408 409
想一想:如果样本的方差为k,那么数据的方差是多少?它的标准差呢?你发现了什么规律?
(2)请你计算下面几组数据的方差:
①1 2 3 4 5 6 7 8 9
②1×2 2×2 3×2 … 9×2
③1×10 2×10 3×10 … 9×10
想一想:如果样本的方差为k,那么数据的方差是多少?它的标准差呢?你发现了什么规律?
解:(1)三组数据的方差均为.
所以如果样本的方差为,那么数据的方差是,它的标准差是.
规律:当把一组数据的每一个数都加上(或减去)同一个数时,这组新数据的方差与标准差和原来据的相同.
(2)三组数据的方差分别为.
如果样本的方差是,它的标准差是.
规律:当一组数据的每一个数都扩大(缩小)原来的倍时,其方差变为原来的倍,标准差变为原来的倍.
11.已知一组数据的方差是2,并且,求x.
解:因为,
所以.
即.
所以.
又,
即,
所以.
12.从甲、乙两种玉米苗中各抽10株,分别测得它们的株高如下:(单位:cm):
甲:25 41 40 37 22 14 19 39 21 42
乙:27 16 44 27 44 16 40 40 16 40
问:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
答案:(1)(cm),
(cm),
所以,所以乙种玉米苗长得高.
(2)
.
,
所以.故甲种玉米长得齐.
一、选择题
1.下列叙述中正确的是( )
A.从频率分布表可以看出样本数据对于平均数的波动大小
B.频数是指落在各个小组内的数据
C.每小组的频数与样本容量之比是这个小组的频率
D.组数是样本平均数除以组距
答案:C
2.如果五个数的平均数是7,那么这五个数的平均数是( )
A.5 B.6 C.7 D.8
答案:D
3.为了让人们感受到丢弃塑料袋对环境造成的影响,某班环保小组的六名同学记录了自己家中一周内丢弃的塑料袋的数量,结果如下(单位:个):33、25、28、26、25、31,如果该班有45名同学,那么根据提供的数据估计这周全班同学各家总共丢弃塑料袋的数量约为( )
A.900 B.1080 C.1260 D.1800
答案:C
4.一组数据的方差为3,将这组数据中的每一个数据都扩大到原来的3倍,则所得到的一组数据的方差是( )
A.1 B.27 C.9 D.3
答案:B
5.已知两个样本,甲:2,4,6,8,10;乙:1,3,5,7,9.样本方差分别为,则二者的关系是( )
A. B.
C. D.无法确定
答案:C
6.已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么下列样本范围的频率为0.25的是( ).
A.[5.5,7.5) B.[7.5,9.5)
C.[9.5,11.5) D.[11.5,13.5)
21世纪教育网
答案:D
二、填空题
7.一个容量为n的样本分成若干组,已知某组的频数和频率分别为30和0.25,则 .
答案:120
8.一个容量为20的样本数据,分组后,组距和频数如下:[10,20),2;[20,30),3;
[30,40),4;[40,50),5;[50,60),4;[60,70],2.则样本数据在区间[50,+∞)上的频率为 .
答案:0.3
9.五个数1,2,3,4,a的平均数是3,则这五个数的标准差是 .
答案:
10.某人射击十次,得环数如下:18,20,19,22,20,21,19,19,20,21,则这组数据的平均数是 ,方差是 .
答案:19.9,1.29
三、解答题
11.下表是60名学生的数学成绩的分组情况表:
分组
0.5~0.25
20.5~40.5[21世纪教育网
40.5~60.5
60.5~80.5
80.5~100.5
频数
3
6
12
频率
0.3
(1)在表中空格内填上相应数据;
(2)画出频率分布直方图.
解:(1)
分组
0.5~0.25
20.5~40.5
40.5~60.5
60.5~80.5
80.5~100.5
频数
3
6
12
21
18
频率
0.05
0.10
0.20
0.35
0.3
(2)频率分布直方图如图所示:
12.2007年是某省实施新课程改革后的第一次高考,经教育部批准该省自主命题,为慎重起见,该省于2005年制定了两套高考方案,且对这两套方案在全省14个地级市分别召集专家进行研讨,并对认为合理的方案进行了投票表决,统计结果如下:
第一套方案:38,25,73,64,20,55,72,41,8,67,70,66,58,24
第二套方案:36,42,6,61,21,54,12,42,5,14,19,19,45,37
用茎叶图说明哪个方案比较稳妥.
解:作茎叶图如下:
21世纪教育网
从茎叶可以看出第一套方案比较稳妥.
13.为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.
(1)参加这次测试的学生数是多少?
(2)如果本次测试身高在157cm以上(包括157cm)的为良好,试估计该校女生身高良好率是多少?
解:(1)由于,故参另这次测试的学生有60名;
(2)由于.
14.要从甲、乙、丙三位射击运动员中选拔一名参加比赛,在预选赛中,他们每人各打10发子弹,命中的环数如下:
甲:1010910999999
乙:1010109108810108
丙:1098108910999
根据这次成绩,应该派谁去参赛?
解:经计算,甲、乙、丙三人命中的总环数分别为93,93,91,所以应先淘汰丙.
设甲、乙平均成绩分别为,方差分别为,则,
,
,
虽然二者总成绩相同,但因为即,故甲的发挥比较稳定,所以应派甲去参赛.
高中苏教数学③2.2~2.3综合测试题
一、选择题
1.下列说法正确的是( ).
A.一组数据的标准差是这组数据的方差的平方
B.一组数据的平均数一定大于这组数据中的每个数据
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.一组数据的方差越大,说明这组数据的波动越大
答案:D
2.10名工人某天生产同一零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12.设其平均数为a,中位数为b,众数为c,则有( )
A. B.
C. D.
答案:D
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.3.5 B. C.3 D.
答案:B
4.两个样本,甲:5,4,3,2,1;乙:4,0,2,1,. 那么样本甲和样本乙的波动大小情况是( )
A.甲、乙波动大小一样
B.甲的波动比乙的波动大
C.乙的波动比甲的波动大21世纪教育网
D.甲、乙的波动大小无法比较
答案:C
二、填空题
5.频率分布扇形图是用圆中扇形面积与圆面积的比来表示各组成部分频率的统计图.现抽查20名学生的血型,结果如下:A,B,A,B,B,O,AB,A,A,O, A,B,A,A,B,AB,O,A,AB,A.则扇形图中表示B型血的扇形的圆心角的度数为 .
答案:
6.已知一个样本方差是,则这个样本的容量
是 ,平均数是 .
答案:10;4
7.已知样本99,100,101,的平均数是100,方差是2,则 .
答案:9996
8.已知样本80,82,84,86,88的方差为,且关于x的方程的两根的平方和恰好是,则 .
答案:
三、解答题
9.质检部门对甲、乙两种日光灯的使用时间进行了破坏性试验,10次试验得到的两种日光灯的使用时间如下两表所示,问:哪一种质量相对好一些?
使用时间(小时)
频数
2100
1
2110
2
212021世纪教育网
3
2130
3
2140
1
甲
使用时间(小时)
频数
2100
1
2110
1
2120
5
2130
2
2140
1
乙
解:(小时),
(小时)
又,
,
故,,
所以乙的质量好一些.
10.(1)计算下面几组数据的方差:
①1 2 3 4 5 6 7 8 9
②101 102 103 104 105 106 107 108 109
③401 402 403 404 405 406 407 408 409
想一想:如果样本的方差为k,那么数据的方差是多少?它的标准差呢?你发现了什么规律?
(2)请你计算下面几组数据的方差:
①1 2 3 4 5 6 7 8 9
②1×2 2×2 3×2 … 9×2
③1×10 2×10 3×10 … 9×10
想一想:如果样本的方差为k,那么数据的方差是多少?它的标准差呢?你发现了什么规律?
解:(1)三组数据的方差均为.
所以如果样本的方差为,那么数据的方差是,它的标准差是.
规律:当把一组数据的每一个数都加上(或减去)同一个数时,这组新数据的方差与标准差和原来据的相同.
(2)三组数据的方差分别为.
如果样本的方差是,它的标准差是.
规律:当一组数据的每一个数都扩大(缩小)原来的倍时,其方差变为原来的倍,标准差变为原来的倍.
11.已知一组数据的方差是2,并且,求x.
解:因为,
所以.
即.
所以.
又,
即,
所以.
12.从甲、乙两种玉米苗中各抽10株,分别测得它们的株高如下:(单位:cm):
甲:25 41 40 37 22 14 19 39 21 42
乙:27 16 44 27 44 16 40 40 16 40
问:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
答案:(1)(cm),
(cm),
所以,所以乙种玉米苗长得高.
(2)
.
,
所以.故甲种玉米长得齐.
