(新人教b版必修3)数学:第二章《统计-单元综合》测试
文档属性
| 名称 | (新人教b版必修3)数学:第二章《统计-单元综合》测试 |

|
|
| 格式 | rar | ||
| 文件大小 | 64.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-14 00:00:00 | ||
图片预览



文档简介
概率与统计综合测试卷
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一所中学有高一、高二、高三共三个年级的学生1600名,其中高三学生400名.如果通过分层抽样的方法从全体高中学生中抽取一个容量为80人的样本,那么应当从高三年级的学生中抽取的人数是( )
A.10 B.20 C. 30 D.40
2.从总体中抽取的样本数据共有m个a,n个b,p个c,则总体的平均数的估计值为( )
A. B. C. D.
3.甲、乙两人独立地解同一问题,甲解出这个问题的概率是,乙解出这个问题的概率是,那么其中至少有1人解出这个问题的概率是( )
A. B. C. D.
4.若的展开式中各项的系数和为128,则项的系数为( )
A.189 B.252 C.-189 D.-252
5.甲、乙、丙、丁四名射击选手在选拨赛中所得的
甲
乙
丙
丁
8
9
9
8
S2
5.7
6.2
5.7
6.4
平均环数及其方差S2如下表所示,则选送参加
决赛的最佳人选是
A.甲 B.乙 C.丙 D.丁
6.已知n为奇数,且n≥3,那么被9除所得的余数是( )
A.0 B.1 C.7 D.8
7.某仪表显示屏上有一排八个编号小孔,每个小孔可显示红或绿两种颜色灯光.若每次有且只有三个小孔可以显示,但相邻小孔不能同时显示,则每次可以显示( )种不同的结果.
A.20 B.40 C.80 D.160
8.现有20个零件,其中16个一等品,4个二等品.若从20个零件中任取2个,那么至少有一个是一等品的概率是( )
A. B. C. D.
9.七张卡片上分别写有0、0、1、2、3、4、5,现从中取出三张后排成一排,组成一个三位数,则共能组成( )个不同的三位数.
A.100 B.105 C.145 D.150
10.把一枚质地不均匀的硬币连掷5次,若恰有一次正面向上的概率和恰有两次正面向上的概率相同(均不为0也不为1),则恰有三次正面向上的概率是( )
A. B. C. D.
二.填空题:本大题共6小题,每小题5分,共30分.
11.某住宅小区有居民2万户,从中随机抽取200户,调查是否安装宽带,调查结果如下表所示:
宽带
动迁户
原住户
已安装
60
35
未安装
45
60
则该小区已安装宽带的户数估计有 户
12.如下是一个容量为200的样本的频率分布直方图,根据图中数据填空:[来源:21世纪教育网]
(1)样本数据落在范围[5,9)的频率为_______;
(2)样本数据落在范围[9,13)的频数为_______.
13.在某市高三数学统考的抽样调查中,对90分
以上(含90分)的成绩进行统计,其频率分布图如
图所示,若130~140分数段的人数为90人,则90~
100分数段的人数为_____________人.
14.方程的解集是____________________.
15.若某人投篮的命中率为p,则他在第n次投篮才首次命中的概率是________________.
16.从1到10这10个数中任取不同的三个数,相加后能被3整除的概率是_____________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)有A、B、C、D四封信和1号、2号、3号三个信箱,若四封信可以随意投入信箱,投完为止.(1)求3号信箱恰好有一封信的概率;(2)求A信没有投入1号信箱的概率.
18.(本小题满分12分)一个口袋中装有三个红球和两个白球.第一步:从口袋中任取两个球,放入一个空箱中;第二步:从箱中任意取出一个球,记下颜色后放回箱中.若进行完第一步后,再重复进行三次第二步操作,分别求出从箱中取出一个红球、两个红球.
19.(本小题满分12分)若非零实数m、n满足2m+n=0,且在二项式(a>0,b>0)的展开式中当且仅当常数项是系数最大的项,(1)求常数项是第几项;(2)求的取值范围.
20.(本小题满分12分)在一次由甲、乙、丙三人参加的围棋争霸赛中,比赛按以下规则进行,第一局:甲对乙;第二局:第一局胜者对丙;第三局:第二局胜者对第一局败者;第四局:第三局胜者对第二局败者.根据以往战绩可知,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,(1)求比赛以乙连胜四局而告终的概率;(2)求比赛以丙连胜三局而告终的概率.
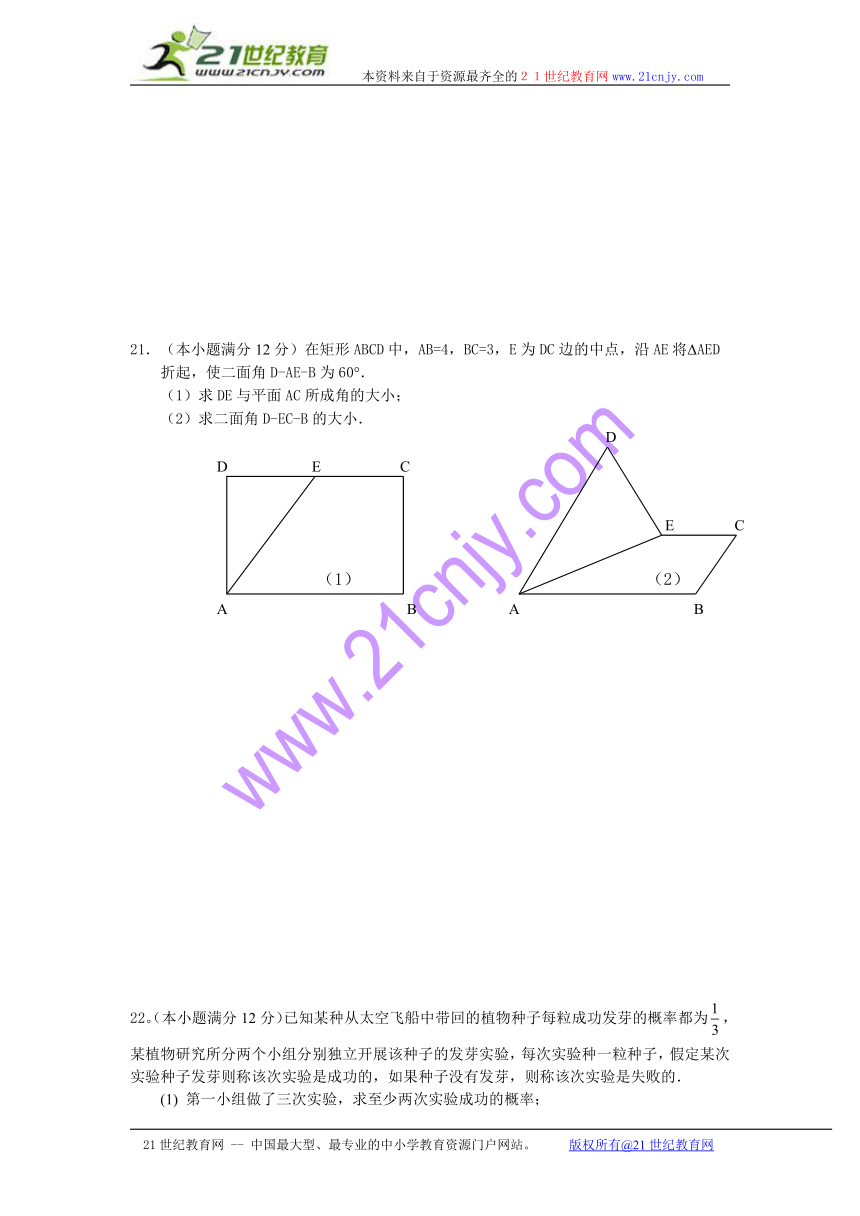
21.(本小题满分12分)在矩形ABCD中,AB=4,BC=3,E为DC边的中点,沿AE将ΔAED
折起,使二面角D-AE-B为60°. (1)求DE与平面AC所成角的大小; (2)求二面角D-EC-B的大小.
(1) (2)
21世纪教育网
22。(本小题满分12分)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
(1) 第一小组做了三次实验,求至少两次实验成功的概率;
(2) 第二小组进行试验,到成功了4次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率.
21世纪教育网
一.B、D、D、C、C C、D、D、B、A
二.(11)9500; (12)0.32,72; (13)810;(14){1,3};(15); (16)21世纪教育网
三.(17) (1)设3号信箱恰好有一封信的概率为P1, -------(1分)
则P1 == ; ------(5分)
(2)设A信没有投入1号信箱的概率为P2, -------(6分)
则 . ------(10分)
(18)设从箱中取出一个红球、两个红球、三个红球的概率分别为 ----(1分)
从箱中取出一个红球时,完成事件只有一种可能:第一步取出的2个球1红1白,此时事件发生的概率为 --------(6分)
从箱中取出两个红球时,完成事件只有一种可能:第一步取出的2个球1红1白,此时事件发生的概率为 -------(12分)
解法二:
设从箱中取出一个红球、两个红球、三个红球的概率分别为 ----(1分)
第一步操作结束后,箱子中没有红球的概率为,箱子中有1个红球的概率为,箱子中有2个红球的概率为, -------(5分)
则, --------(8分)
, --------(12分)
(19)(1)设为常数项, ------(1分)
则可由 ------(3分)
解得 r=4, ------(5分)
所以常数项是第5项. ------(6分)
(2)由只有常数项为最大项且a>0,b>0,
可得 -------(10分)
解得 ------(12分)
(20)(1)设乙连胜四局的概率为,
则 -------(6分)
(2)设丙连胜三局的概率为,
则 ------(12分)
(21)解:(1)在图(2)中,作平面,为垂足,
作,为垂足,连结,则
∴为二面角的平面角
∴
在中,
在中,
∵平面
∴为与平面所成的角
------------(6分)
(2)在图(2)中过作于,为垂足,连结,则
∴为二面角的平面角
则
∴
∴二面角的平面角为。----------(12分)
(22)(1) 第一小组做了三次实验,至少两次实验成功的概率是
.------------(6分)
(2) 第二小组在第4次成功前,共进行了6次试验,其中三次成功三次失败,且恰有两次连续失败,其各种可能的情况种数为.因此所求的概率为
. ----------(12分)
21世纪教育网
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一所中学有高一、高二、高三共三个年级的学生1600名,其中高三学生400名.如果通过分层抽样的方法从全体高中学生中抽取一个容量为80人的样本,那么应当从高三年级的学生中抽取的人数是( )
A.10 B.20 C. 30 D.40
2.从总体中抽取的样本数据共有m个a,n个b,p个c,则总体的平均数的估计值为( )
A. B. C. D.
3.甲、乙两人独立地解同一问题,甲解出这个问题的概率是,乙解出这个问题的概率是,那么其中至少有1人解出这个问题的概率是( )
A. B. C. D.
4.若的展开式中各项的系数和为128,则项的系数为( )
A.189 B.252 C.-189 D.-252
5.甲、乙、丙、丁四名射击选手在选拨赛中所得的
甲
乙
丙
丁
8
9
9
8
S2
5.7
6.2
5.7
6.4
平均环数及其方差S2如下表所示,则选送参加
决赛的最佳人选是
A.甲 B.乙 C.丙 D.丁
6.已知n为奇数,且n≥3,那么被9除所得的余数是( )
A.0 B.1 C.7 D.8
7.某仪表显示屏上有一排八个编号小孔,每个小孔可显示红或绿两种颜色灯光.若每次有且只有三个小孔可以显示,但相邻小孔不能同时显示,则每次可以显示( )种不同的结果.
A.20 B.40 C.80 D.160
8.现有20个零件,其中16个一等品,4个二等品.若从20个零件中任取2个,那么至少有一个是一等品的概率是( )
A. B. C. D.
9.七张卡片上分别写有0、0、1、2、3、4、5,现从中取出三张后排成一排,组成一个三位数,则共能组成( )个不同的三位数.
A.100 B.105 C.145 D.150
10.把一枚质地不均匀的硬币连掷5次,若恰有一次正面向上的概率和恰有两次正面向上的概率相同(均不为0也不为1),则恰有三次正面向上的概率是( )
A. B. C. D.
二.填空题:本大题共6小题,每小题5分,共30分.
11.某住宅小区有居民2万户,从中随机抽取200户,调查是否安装宽带,调查结果如下表所示:
宽带
动迁户
原住户
已安装
60
35
未安装
45
60
则该小区已安装宽带的户数估计有 户
12.如下是一个容量为200的样本的频率分布直方图,根据图中数据填空:[来源:21世纪教育网]
(1)样本数据落在范围[5,9)的频率为_______;
(2)样本数据落在范围[9,13)的频数为_______.
13.在某市高三数学统考的抽样调查中,对90分
以上(含90分)的成绩进行统计,其频率分布图如
图所示,若130~140分数段的人数为90人,则90~
100分数段的人数为_____________人.
14.方程的解集是____________________.
15.若某人投篮的命中率为p,则他在第n次投篮才首次命中的概率是________________.
16.从1到10这10个数中任取不同的三个数,相加后能被3整除的概率是_____________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)有A、B、C、D四封信和1号、2号、3号三个信箱,若四封信可以随意投入信箱,投完为止.(1)求3号信箱恰好有一封信的概率;(2)求A信没有投入1号信箱的概率.
18.(本小题满分12分)一个口袋中装有三个红球和两个白球.第一步:从口袋中任取两个球,放入一个空箱中;第二步:从箱中任意取出一个球,记下颜色后放回箱中.若进行完第一步后,再重复进行三次第二步操作,分别求出从箱中取出一个红球、两个红球.
19.(本小题满分12分)若非零实数m、n满足2m+n=0,且在二项式(a>0,b>0)的展开式中当且仅当常数项是系数最大的项,(1)求常数项是第几项;(2)求的取值范围.
20.(本小题满分12分)在一次由甲、乙、丙三人参加的围棋争霸赛中,比赛按以下规则进行,第一局:甲对乙;第二局:第一局胜者对丙;第三局:第二局胜者对第一局败者;第四局:第三局胜者对第二局败者.根据以往战绩可知,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,(1)求比赛以乙连胜四局而告终的概率;(2)求比赛以丙连胜三局而告终的概率.
21.(本小题满分12分)在矩形ABCD中,AB=4,BC=3,E为DC边的中点,沿AE将ΔAED
折起,使二面角D-AE-B为60°. (1)求DE与平面AC所成角的大小; (2)求二面角D-EC-B的大小.
(1) (2)
21世纪教育网
22。(本小题满分12分)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
(1) 第一小组做了三次实验,求至少两次实验成功的概率;
(2) 第二小组进行试验,到成功了4次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率.
21世纪教育网
一.B、D、D、C、C C、D、D、B、A
二.(11)9500; (12)0.32,72; (13)810;(14){1,3};(15); (16)21世纪教育网
三.(17) (1)设3号信箱恰好有一封信的概率为P1, -------(1分)
则P1 == ; ------(5分)
(2)设A信没有投入1号信箱的概率为P2, -------(6分)
则 . ------(10分)
(18)设从箱中取出一个红球、两个红球、三个红球的概率分别为 ----(1分)
从箱中取出一个红球时,完成事件只有一种可能:第一步取出的2个球1红1白,此时事件发生的概率为 --------(6分)
从箱中取出两个红球时,完成事件只有一种可能:第一步取出的2个球1红1白,此时事件发生的概率为 -------(12分)
解法二:
设从箱中取出一个红球、两个红球、三个红球的概率分别为 ----(1分)
第一步操作结束后,箱子中没有红球的概率为,箱子中有1个红球的概率为,箱子中有2个红球的概率为, -------(5分)
则, --------(8分)
, --------(12分)
(19)(1)设为常数项, ------(1分)
则可由 ------(3分)
解得 r=4, ------(5分)
所以常数项是第5项. ------(6分)
(2)由只有常数项为最大项且a>0,b>0,
可得 -------(10分)
解得 ------(12分)
(20)(1)设乙连胜四局的概率为,
则 -------(6分)
(2)设丙连胜三局的概率为,
则 ------(12分)
(21)解:(1)在图(2)中,作平面,为垂足,
作,为垂足,连结,则
∴为二面角的平面角
∴
在中,
在中,
∵平面
∴为与平面所成的角
------------(6分)
(2)在图(2)中过作于,为垂足,连结,则
∴为二面角的平面角
则
∴
∴二面角的平面角为。----------(12分)
(22)(1) 第一小组做了三次实验,至少两次实验成功的概率是
.------------(6分)
(2) 第二小组在第4次成功前,共进行了6次试验,其中三次成功三次失败,且恰有两次连续失败,其各种可能的情况种数为.因此所求的概率为
. ----------(12分)
21世纪教育网
