(苏教版必修3)数学:2.3-2《总体分布的估计》课件
文档属性
| 名称 | (苏教版必修3)数学:2.3-2《总体分布的估计》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 424.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-14 08:41:00 | ||
图片预览





文档简介
课件20张PPT。总体分布的估计(2)复习回顾:1.频数与频率 频数是指一组数据中,某范围内的数据出现的次数;把频数除以数据的总个数,就得到频率.2.频率分布表 当总体很大或不便于获得时,可以用样本的频率分布估计总体的频率分布.我们把反映总体频率分布的表格称为频率分布表.S1 作出频率分布表,然后作直角坐标系,以横轴表示数据,纵
轴表示“频率/组距”;
S2 把横轴分为若干段,每一线段对应一个组的组距,
S3 以此线段为底作一矩形,它的高等于该组的频率/组距,这样得
出一系列的矩形,每个矩形的面积恰好是该组上的频率.
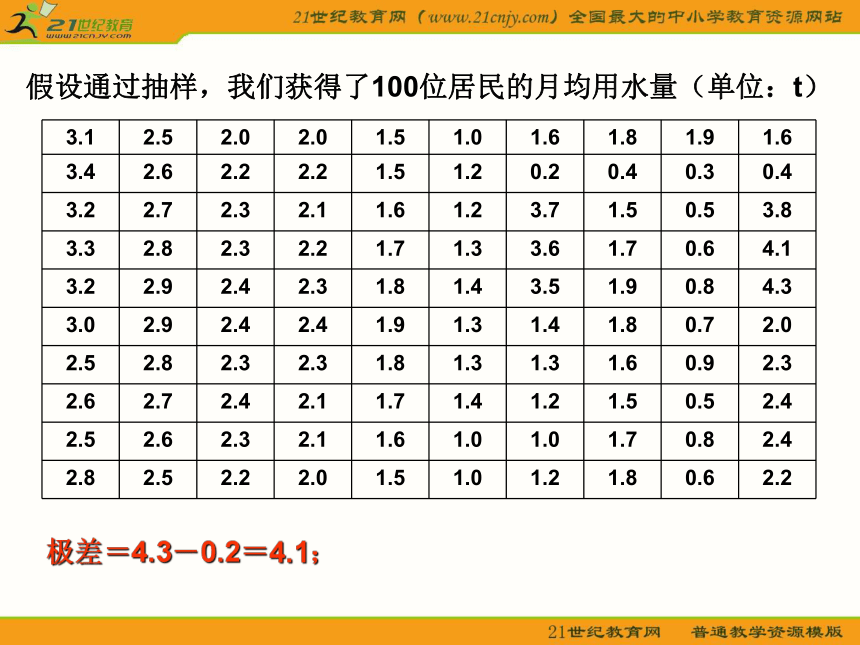
这些矩形就构成了频率分布直方图. 所有矩形的面积和为1 .算法:3.频率分布直方图 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.如果希望大部分居民的日常生活不受影响,那么a定为多少比较合理?问题引入: 例1:某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费。 ①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢? ②为了较合理地确定这个标准,你认为需要做
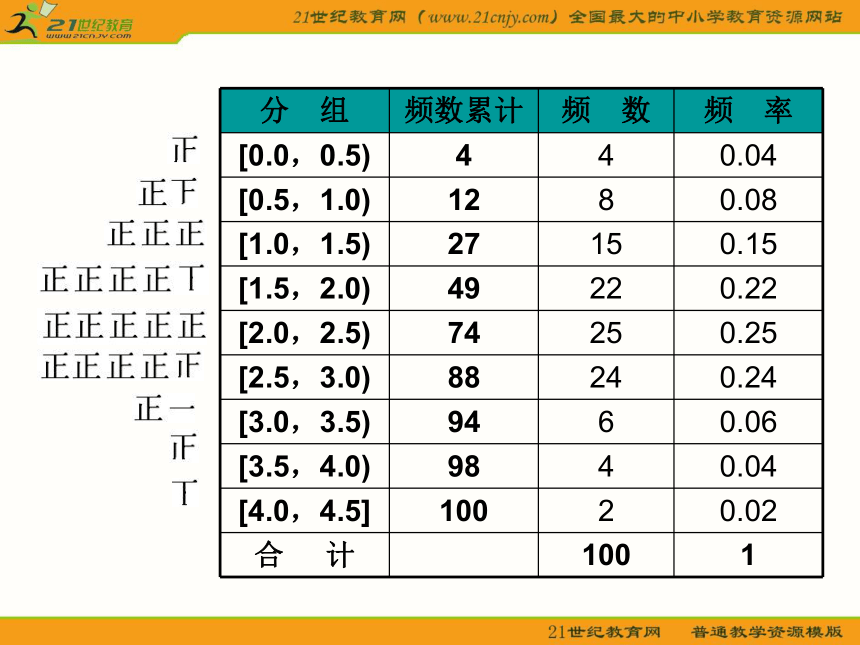
哪些工作?假设通过抽样,我们获得了100位居民的月均用水量(单位:t)极差=4.3-0.2=4.1;极差=4.3-0.2=4.1;如果取区间[0.15,4.35],则全距为4.2;
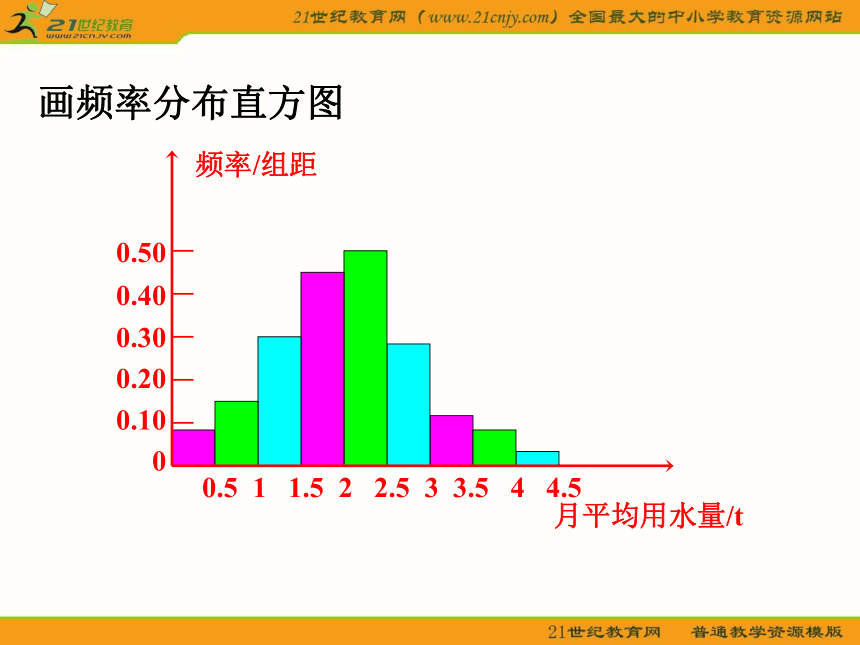
分10组,组距为0.42因此分9组,全距为4.5,取区间[0,4.5]为了方便起见,组距尽可能“取整”,因此定为0.5!画频率分布直方图同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的图的性状也会不同.不同的形状给人不同的印象,这种印象会影响我们对总体的判断.从图中我们可以看到,月均用水量在区间[2,2.5)内的居民最多,在[1.5,2)内次之,大部分居民的月均用水量都在[1,3)之间. 直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到分布表中看不清楚的数据模式,但是直观图也丢失了一些信息,例如,原始数据不能在图中表示出了.频率分布折线图 如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连结起来,就得到一条折线,我们称这条折线为本组数据的频率折线图.频率折线图的优点是它反映了数据的变化趋势.如果将样本容量取得足够大,分组的组距取得足够小,则这条折线将趋于一条曲线,我们称这一曲线为总体分布的密度曲线.总体密度曲线 某篮球运动员在某赛季各场比赛的得分情况如下:
12,15,24,25,31,31,36,36,37,39,44,49,501
2
3
4
5←叶:表示个位数字茎:表示十位数字→茎叶图2545166794901从这张图可以粗略地看出,该运动员平均得分及中位数、众数都在20到40之间,且分布较对称,集中程度高,说明其发挥比较稳定.茎叶图的画法:
将所有的两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.
茎叶图的优缺点:
优点是所有的信息都可以从茎叶图中得到,便于记录和表示.但茎叶图表示三位或三位以上的数据时不够方便. 某医院的发热门诊部对一天接待的16名病人的体温进行了测量,得到以下数据:
37.5,38.0,39.2,38.5,39.5,37.8,39.1,38.2,37.6,39.2,38.1,39.5,37.8,38.5,38.7,39.3
请作出当天病人体温的茎叶图,并计算出病人的平均体温.课堂小结:1.频率分布直方图2.频率分布折线图——总体分布的密度曲线总体密度曲线3.茎叶图1
2
3
4
5←叶:表示个位数字茎:表示十位数字→将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从小到大(或从大到小)的顺序同行列出.25
45
116679
49
0
轴表示“频率/组距”;
S2 把横轴分为若干段,每一线段对应一个组的组距,
S3 以此线段为底作一矩形,它的高等于该组的频率/组距,这样得
出一系列的矩形,每个矩形的面积恰好是该组上的频率.
这些矩形就构成了频率分布直方图. 所有矩形的面积和为1 .算法:3.频率分布直方图 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.如果希望大部分居民的日常生活不受影响,那么a定为多少比较合理?问题引入: 例1:某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费。 ①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢? ②为了较合理地确定这个标准,你认为需要做
哪些工作?假设通过抽样,我们获得了100位居民的月均用水量(单位:t)极差=4.3-0.2=4.1;极差=4.3-0.2=4.1;如果取区间[0.15,4.35],则全距为4.2;
分10组,组距为0.42因此分9组,全距为4.5,取区间[0,4.5]为了方便起见,组距尽可能“取整”,因此定为0.5!画频率分布直方图同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的图的性状也会不同.不同的形状给人不同的印象,这种印象会影响我们对总体的判断.从图中我们可以看到,月均用水量在区间[2,2.5)内的居民最多,在[1.5,2)内次之,大部分居民的月均用水量都在[1,3)之间. 直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到分布表中看不清楚的数据模式,但是直观图也丢失了一些信息,例如,原始数据不能在图中表示出了.频率分布折线图 如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连结起来,就得到一条折线,我们称这条折线为本组数据的频率折线图.频率折线图的优点是它反映了数据的变化趋势.如果将样本容量取得足够大,分组的组距取得足够小,则这条折线将趋于一条曲线,我们称这一曲线为总体分布的密度曲线.总体密度曲线 某篮球运动员在某赛季各场比赛的得分情况如下:
12,15,24,25,31,31,36,36,37,39,44,49,501
2
3
4
5←叶:表示个位数字茎:表示十位数字→茎叶图2545166794901从这张图可以粗略地看出,该运动员平均得分及中位数、众数都在20到40之间,且分布较对称,集中程度高,说明其发挥比较稳定.茎叶图的画法:
将所有的两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.
茎叶图的优缺点:
优点是所有的信息都可以从茎叶图中得到,便于记录和表示.但茎叶图表示三位或三位以上的数据时不够方便. 某医院的发热门诊部对一天接待的16名病人的体温进行了测量,得到以下数据:
37.5,38.0,39.2,38.5,39.5,37.8,39.1,38.2,37.6,39.2,38.1,39.5,37.8,38.5,38.7,39.3
请作出当天病人体温的茎叶图,并计算出病人的平均体温.课堂小结:1.频率分布直方图2.频率分布折线图——总体分布的密度曲线总体密度曲线3.茎叶图1
2
3
4
5←叶:表示个位数字茎:表示十位数字→将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从小到大(或从大到小)的顺序同行列出.25
45
116679
49
0
