(新人教b版必修3)数学:1.1.3《算法的三种基本逻辑结构和框图表示》课件1
文档属性
| 名称 | (新人教b版必修3)数学:1.1.3《算法的三种基本逻辑结构和框图表示》课件1 |

|
|
| 格式 | rar | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-14 00:00:00 | ||
图片预览






文档简介
课件23张PPT。1.1.3算法的三种基本逻辑结构和框图表示(二) 在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.
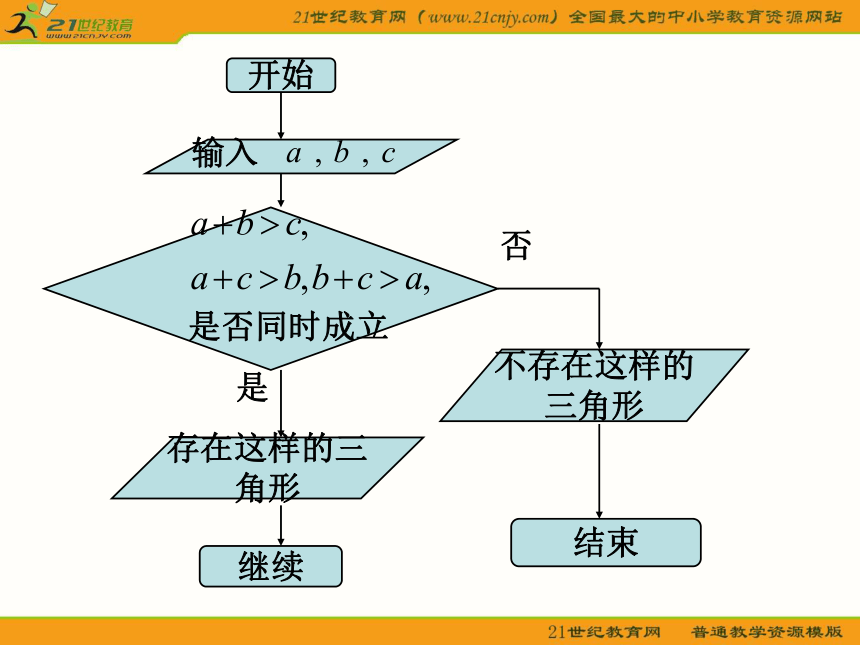
例如在上一节课中,我们作过一个求三角形的面积的流程,其实那个流程是有问题的。因为当输入了a,b,c三个数值后,我们不知道它们是否可以组成三角形。所以应该先作一个判断,如果是三角形,则继续去计算面积;如果不是三角形,则输出错误信息。开始存在这样的三
角形继续不存在这样的
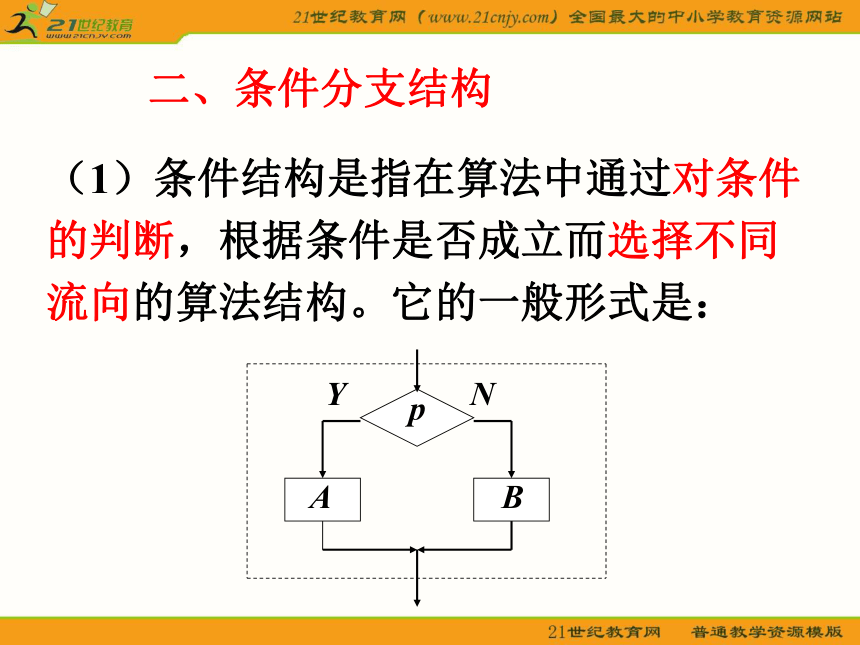
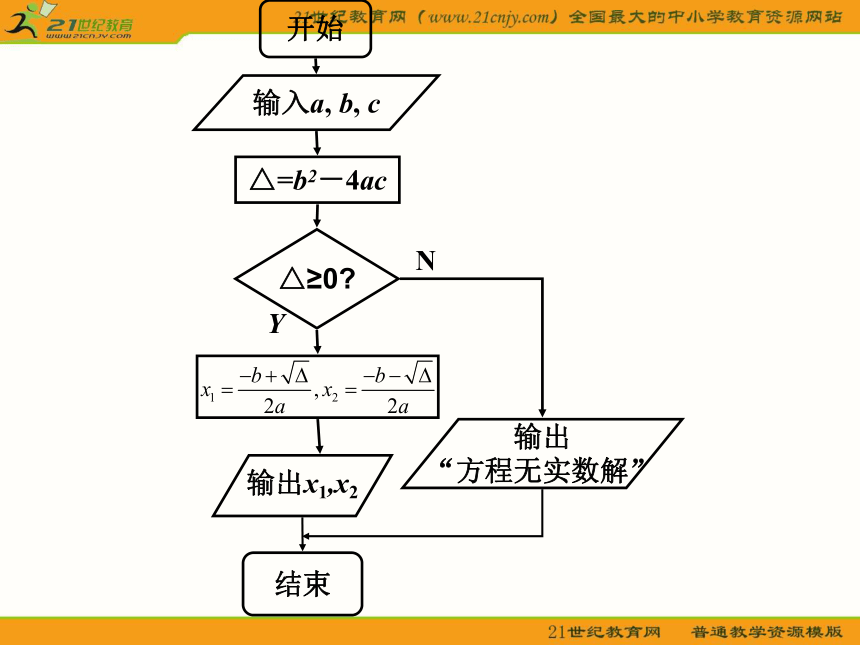
三角形是否结束二、条件分支结构(1)条件结构是指在算法中通过对条件的判断,根据条件是否成立而选择不同流向的算法结构。它的一般形式是:(2)此结构中包含一个判断框,根据给定的条件P是否成立而选择执行A框或B框。无论P条件是否成立,只能执行A框或B框之一。(3)一个判断结构可以有多个判断框。(4)在许多算法中,需要对问题的条件作出逻辑判断,判断后依据条件是否成立而进行不同的处理方式,这就需要用条件结构来实现算法。例1.解一元二次方程ax2+bx+c=0.S1 计算△=b2-4ac;S2 如果△<0,则原方程无实数解;S3 输出x1,x2,或“无实数解”信息.△=b2-4ac输出x1,x2△≥0?YN输出
“方程无实数解”输入a, b, c开始结束例2.设火车托运重量为P(kg)行李时,每千米的费用(单位:元)标准为
画出行李托运费用的程序框图。解:先输入托运的重量P和里程D,再分别用各自的条件下的计算公式来计算处理。 然后将结果与托运路程D相乘,最后输出托运行李的费用M。否是开始输入P、DP>30Y=0.3×30+0.5(P-30)Y=0.3PM=D×Y输出M结束 由此可见,在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向,这种先根据条件作出判断,再决定执行哪一种操作的结构就是条件分支结构,条件分支结构又称为条件结构。在A或B两个框中可以有一个是空的,即不执行任何操作,如图也是条件结构的一种.例3. 求过两点P1(x1,y1),P2(x2,y2)的直线的斜率,设计该问题的算法并画出程序框图。 解:由于当x1=x2时,过两点P1、P2的直线的斜率不存在,只有当x1≠x2时,才可根据斜率公式求出,故可设计如下的算法和程序框图. S1 输入x1,y1,x2,y2;
S2 如果x1=x2,输出“ 斜率不存在”;S3 输出k.例4、设计求一个数x的绝对值的算法,并画出相应的程序框图。解:算法如下:
S1:输入x;
S2:如果x≥0,则y=x,
否则, y =-x;
S3:输出y 。结 束YN开始输入xx≥0?输出y y=xy=-x例5. 下面的流程图表示了一个什么样的算法? 开始输入a,b,ca>b且a>cb>cYNYN输出a输出c输出b结束例6. 超市购物:
购物不足250元的,无折扣
购物满250元(含,下同),不足500元的,打九五折
购物满500元,不足1000元的,打九折
购物满1000元,打八五折
试画出此算法的流程图. 开始输入x结束输出xx<250x<500x<1000x=x*0.95x=x*0.9x=x*0.85是否是否是否算法课堂练习1.如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法的过程。算法课堂练习2.下面的流程图表示了一个什么样的算法? 所给流程图描述了求三个数a,b,c的最大数的算法。算法课堂练习3.写出解方程ax+b=0(a,b为常数)的算法,并画出流程图。 S1 输入a,b;S2 若a≠0,则x←-b/a,并输出x;解 算法如下:否则,如果b≠0,那么输出“无解”;否则,输出“解为全体实数”.算法课堂练习4.下边的程序框图(如图所示),能判断任意输入的数x的奇偶性,其中判断框内的条件是( )
A. m=0 B. x=0
C. x=1 D. m=15.选择结构不同于顺序结构的特征是含有( )
A.处理框
B.判断框
C.输入、输出框
D.起、止框AB老三课件库算法课堂练习6.设计计算13+33+53+…+993的算法程序,并画出相应的流程图。 算法如下: p=0; i =1;S1S2S3p=p +i 3;S4i =i+2;S5若i >99,则输出p,否则转S3.算法课堂小结1.选择结构的概念:
先根据条件作出判断,再决定执行哪一种操作的结构称为选择结构.
2.理解选择结构的逻辑以及框图的规范画法,选择结构主要用在判断、分类或分情况的问题解决中.
例如在上一节课中,我们作过一个求三角形的面积的流程,其实那个流程是有问题的。因为当输入了a,b,c三个数值后,我们不知道它们是否可以组成三角形。所以应该先作一个判断,如果是三角形,则继续去计算面积;如果不是三角形,则输出错误信息。开始存在这样的三
角形继续不存在这样的
三角形是否结束二、条件分支结构(1)条件结构是指在算法中通过对条件的判断,根据条件是否成立而选择不同流向的算法结构。它的一般形式是:(2)此结构中包含一个判断框,根据给定的条件P是否成立而选择执行A框或B框。无论P条件是否成立,只能执行A框或B框之一。(3)一个判断结构可以有多个判断框。(4)在许多算法中,需要对问题的条件作出逻辑判断,判断后依据条件是否成立而进行不同的处理方式,这就需要用条件结构来实现算法。例1.解一元二次方程ax2+bx+c=0.S1 计算△=b2-4ac;S2 如果△<0,则原方程无实数解;S3 输出x1,x2,或“无实数解”信息.△=b2-4ac输出x1,x2△≥0?YN输出
“方程无实数解”输入a, b, c开始结束例2.设火车托运重量为P(kg)行李时,每千米的费用(单位:元)标准为
画出行李托运费用的程序框图。解:先输入托运的重量P和里程D,再分别用各自的条件下的计算公式来计算处理。 然后将结果与托运路程D相乘,最后输出托运行李的费用M。否是开始输入P、DP>30Y=0.3×30+0.5(P-30)Y=0.3PM=D×Y输出M结束 由此可见,在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向,这种先根据条件作出判断,再决定执行哪一种操作的结构就是条件分支结构,条件分支结构又称为条件结构。在A或B两个框中可以有一个是空的,即不执行任何操作,如图也是条件结构的一种.例3. 求过两点P1(x1,y1),P2(x2,y2)的直线的斜率,设计该问题的算法并画出程序框图。 解:由于当x1=x2时,过两点P1、P2的直线的斜率不存在,只有当x1≠x2时,才可根据斜率公式求出,故可设计如下的算法和程序框图. S1 输入x1,y1,x2,y2;
S2 如果x1=x2,输出“ 斜率不存在”;S3 输出k.例4、设计求一个数x的绝对值的算法,并画出相应的程序框图。解:算法如下:
S1:输入x;
S2:如果x≥0,则y=x,
否则, y =-x;
S3:输出y 。结 束YN开始输入xx≥0?输出y y=xy=-x例5. 下面的流程图表示了一个什么样的算法? 开始输入a,b,ca>b且a>cb>cYNYN输出a输出c输出b结束例6. 超市购物:
购物不足250元的,无折扣
购物满250元(含,下同),不足500元的,打九五折
购物满500元,不足1000元的,打九折
购物满1000元,打八五折
试画出此算法的流程图. 开始输入x结束输出xx<250x<500x<1000x=x*0.95x=x*0.9x=x*0.85是否是否是否算法课堂练习1.如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法的过程。算法课堂练习2.下面的流程图表示了一个什么样的算法? 所给流程图描述了求三个数a,b,c的最大数的算法。算法课堂练习3.写出解方程ax+b=0(a,b为常数)的算法,并画出流程图。 S1 输入a,b;S2 若a≠0,则x←-b/a,并输出x;解 算法如下:否则,如果b≠0,那么输出“无解”;否则,输出“解为全体实数”.算法课堂练习4.下边的程序框图(如图所示),能判断任意输入的数x的奇偶性,其中判断框内的条件是( )
A. m=0 B. x=0
C. x=1 D. m=15.选择结构不同于顺序结构的特征是含有( )
A.处理框
B.判断框
C.输入、输出框
D.起、止框AB老三课件库算法课堂练习6.设计计算13+33+53+…+993的算法程序,并画出相应的流程图。 算法如下: p=0; i =1;S1S2S3p=p +i 3;S4i =i+2;S5若i >99,则输出p,否则转S3.算法课堂小结1.选择结构的概念:
先根据条件作出判断,再决定执行哪一种操作的结构称为选择结构.
2.理解选择结构的逻辑以及框图的规范画法,选择结构主要用在判断、分类或分情况的问题解决中.
