(新人教b版必修3)3.3.1 几何概型
文档属性
| 名称 | (新人教b版必修3)3.3.1 几何概型 |

|
|
| 格式 | rar | ||
| 文件大小 | 473.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-06 00:00:00 | ||
图片预览





文档简介
课件20张PPT。3.3.1几何概型
知识回顾古典概型的特点:1.试验中所有可能出现的基本事件只有有限个.(有限性)
2.每个基本事件出现的可能性相等.(等可能性)古典概型的计算公式:现实生活中,有没有实验的所有可能结果是无穷多的情况?相应的概率如何求?
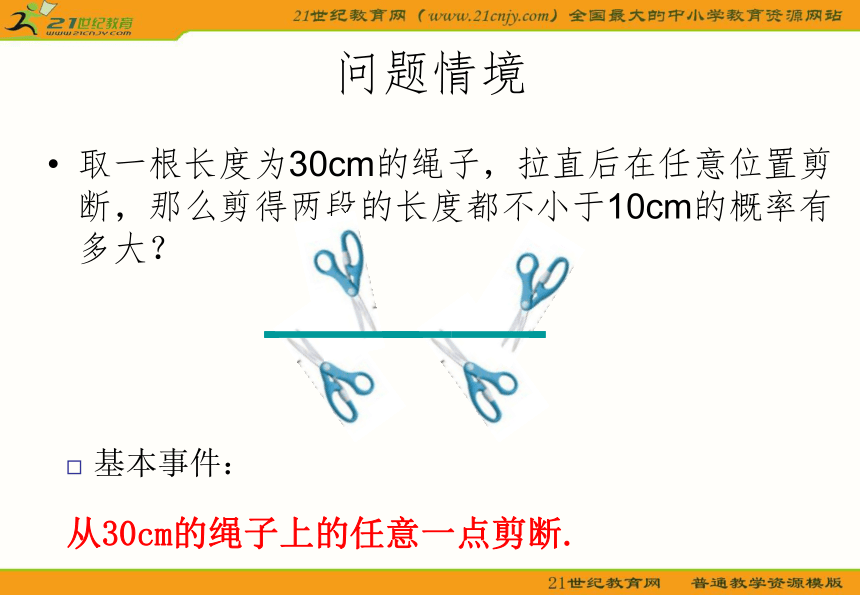
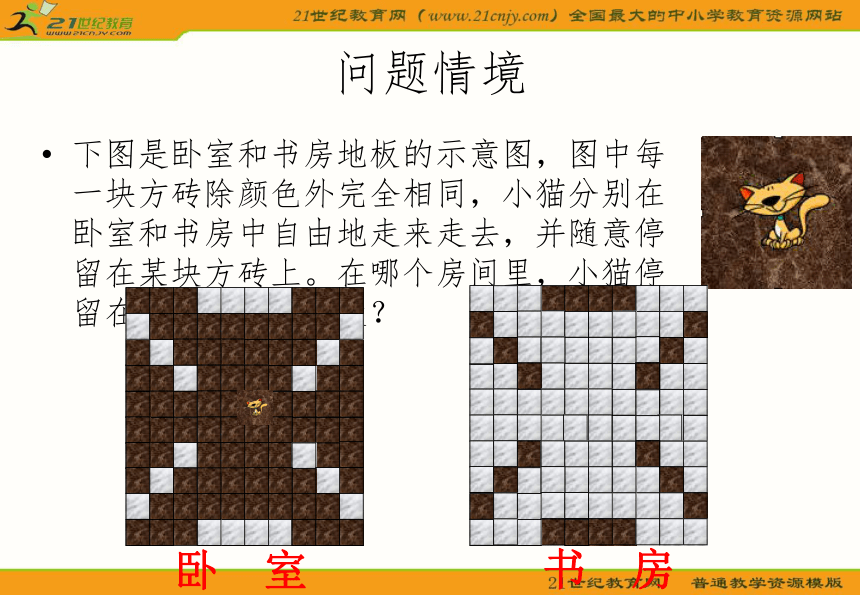
问题情境取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?基本事件:从30cm的绳子上的任意一点剪断.问题情境下图是卧室和书房地板的示意图,图中每一块方砖除颜色外完全相同,小猫分别在卧室和书房中自由地走来走去,并随意停留在某块方砖上。在哪个房间里,小猫停留在黑砖上的概率大?卧 室书 房问题情境这些个问题能否用古典概型的方法来求解呢?
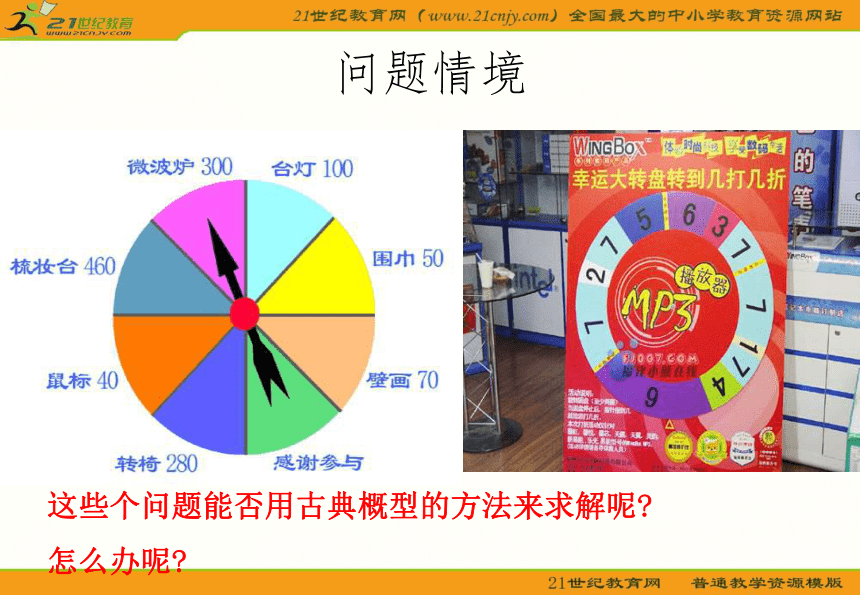
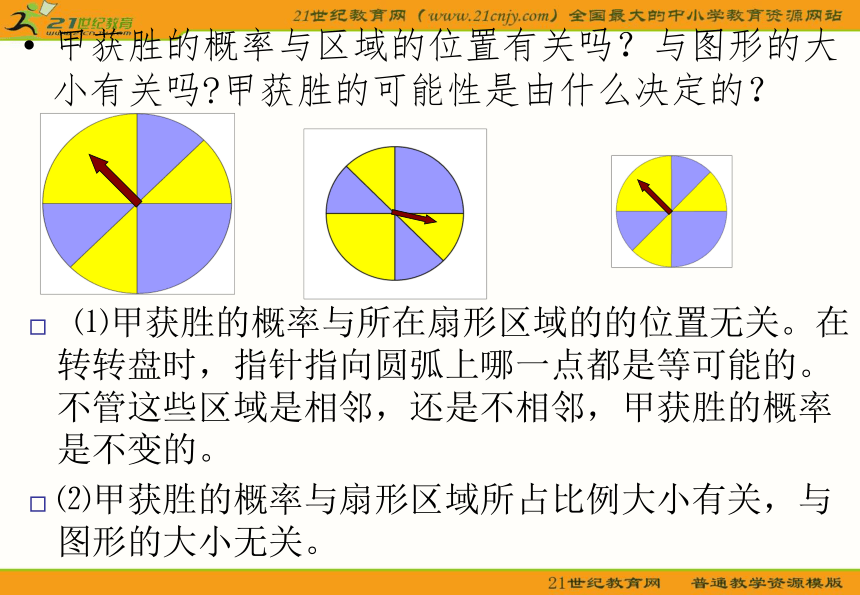
怎么办呢?问题情境问题:图中有两个转盘,甲乙两人玩转盘游戏,规定当指针指向黄色区域时,甲获胜,否则乙获胜。在两种情况下分别求甲获胜的概率是多少?(2)甲获胜的概率与区域的位置有关吗?与图形的大小有关吗?甲获胜的可能性是由什么决定的? ⑴甲获胜的概率与所在扇形区域的的位置无关。在转转盘时,指针指向圆弧上哪一点都是等可能的。不管这些区域是相邻,还是不相邻,甲获胜的概率是不变的。
⑵甲获胜的概率与扇形区域所占比例大小有关,与图形的大小无关。概念形成几何概型我们把事件A理解为区域Ω的某一子区域A(如图),A的概率只与子区域A的几何度量(长度、面积或体积)成正比,而与A的位置和形状无关,满足以上条件的试验称为几何概型概念深化几何概型的特点
1.试验中所有可能出现的基本事件有无限个.(无限性)
2.每个基本事件出现的可能性相等.(等可能性)古典概型的特点
1.试验中所有可能出现的基本事件只有有限个.(有限性)
2.每个基本事件出现的可能性相等.(等可能性)相同:两者基本事件发生的可能性都是相等的;
不同:古典概型要求基本事件有有限个,几何概型要求基本事件有无限多个。 概念深化几何概型的计算公式:说明:区域应指“开区域” ,不包含边界点;在区域D内随机取点是指:该点落在D内任何一处都是等可能的,落在任何部分的可能性只与该部分的测度成正比而与其性状位置无关.典型例题例1.取一个边长为2a的正方形及其内切圆,随机向正方形内丢一粒豆子,求豆子落入圆内的概率.典型例题例2:取一根长为3米的绳子,拉直后在任意位置剪断,那么剪得两段的长都不少于1米的概率有多大?解:如上图,记“剪得两段绳子长都不小于1m”为事件A,把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生。由于中间一段的长度等于绳子长的三分之一,所以事件A发生的概率
P(A)=1/3。3m典型例题例3:有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.分析:细菌在这升水中的分布可以看作是随机的,取得0.1升水可作为事件的区域。解:取出0.1升中“含有这个细菌”这一事件记为A,则 当堂检测1.在线段[0,3]上任取一点,则此点坐标大于1的概率是( )
A 、1/3 B 、2/3 C、1/2 D、1/3
2.在等腰直角三角形ABC中,在斜线段AB上任取一点M,则AM的长小于AC的长的概率是__________。
3.如图所示,在直角坐标系xOy内,射线OT落在120°的终边上,任作一条射线OA,则射线OA落在∠xOT内的概率为 。当堂训练4.在1L高产小麦种子中混入了一粒带麦锈病的种子,从中随机取出10mL,含有麦锈病种子的概率是多少?当堂训练5.在1万平方公里的海域中有40平方公里的大陆贮藏着石油.假如在海域中任意一点钻探,钻到油层面的概率是多少?
6.设有一个均匀的陀螺,在其圆周的一半上均匀的刻上区间[0,1]上的诸数字,另一半上均匀的刻上区间[1,3]的诸数字(所有的数字均按大小排列,且0与3重合)。旋转陀螺,求它停下时,其圆周上触及桌面的刻度为于[0.5,1.5]上的概率当堂训练7.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率。打开收音机的时刻位于[50,60]时间段内则事件A发生.由几何概型的求概率公式得
P(A)=(60-50)/60=1/6
即“等待报时的时间不超过10分钟”的概率为1/6.解:记“等待的时间小于10分钟”为事件A,8.已知地铁列车每10min一班,在车站停1min.求乘客到达站台立即乘上车的概率.9.射箭比赛的箭靶是涂有五个彩色的分环.从外向内为白色、黑色、蓝色、红色,靶心是金色,金色靶心叫“黄心”.奥运会的比赛靶面直径为122cm,靶心直径为12.2cm.运动员在70m外射箭,假设每箭都能中靶,且射中靶面内任一点都是等可能的,那么射中黄心的概率是多少?解题方法小结:对于复杂的实际问题,解题的关键是要建立概率模型,找出随机事件与所有基本事件相对应的几何区域,把问题转化为几何概型的问题,利用几何概型公式求解。
课堂小结1.几何概型适用于试验结果是无穷多且事件是等可能发生的概率类型。
2.几何概型主要用于解决长度、面积、体积有关的题目。
3.注意理解几何概型与古典概型的区别。
4.理解如何将实际问题转化为几何概型的问题,利用几何概型公式求解。
2.每个基本事件出现的可能性相等.(等可能性)古典概型的计算公式:现实生活中,有没有实验的所有可能结果是无穷多的情况?相应的概率如何求?
问题情境取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?基本事件:从30cm的绳子上的任意一点剪断.问题情境下图是卧室和书房地板的示意图,图中每一块方砖除颜色外完全相同,小猫分别在卧室和书房中自由地走来走去,并随意停留在某块方砖上。在哪个房间里,小猫停留在黑砖上的概率大?卧 室书 房问题情境这些个问题能否用古典概型的方法来求解呢?
怎么办呢?问题情境问题:图中有两个转盘,甲乙两人玩转盘游戏,规定当指针指向黄色区域时,甲获胜,否则乙获胜。在两种情况下分别求甲获胜的概率是多少?(2)甲获胜的概率与区域的位置有关吗?与图形的大小有关吗?甲获胜的可能性是由什么决定的? ⑴甲获胜的概率与所在扇形区域的的位置无关。在转转盘时,指针指向圆弧上哪一点都是等可能的。不管这些区域是相邻,还是不相邻,甲获胜的概率是不变的。
⑵甲获胜的概率与扇形区域所占比例大小有关,与图形的大小无关。概念形成几何概型我们把事件A理解为区域Ω的某一子区域A(如图),A的概率只与子区域A的几何度量(长度、面积或体积)成正比,而与A的位置和形状无关,满足以上条件的试验称为几何概型概念深化几何概型的特点
1.试验中所有可能出现的基本事件有无限个.(无限性)
2.每个基本事件出现的可能性相等.(等可能性)古典概型的特点
1.试验中所有可能出现的基本事件只有有限个.(有限性)
2.每个基本事件出现的可能性相等.(等可能性)相同:两者基本事件发生的可能性都是相等的;
不同:古典概型要求基本事件有有限个,几何概型要求基本事件有无限多个。 概念深化几何概型的计算公式:说明:区域应指“开区域” ,不包含边界点;在区域D内随机取点是指:该点落在D内任何一处都是等可能的,落在任何部分的可能性只与该部分的测度成正比而与其性状位置无关.典型例题例1.取一个边长为2a的正方形及其内切圆,随机向正方形内丢一粒豆子,求豆子落入圆内的概率.典型例题例2:取一根长为3米的绳子,拉直后在任意位置剪断,那么剪得两段的长都不少于1米的概率有多大?解:如上图,记“剪得两段绳子长都不小于1m”为事件A,把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生。由于中间一段的长度等于绳子长的三分之一,所以事件A发生的概率
P(A)=1/3。3m典型例题例3:有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.分析:细菌在这升水中的分布可以看作是随机的,取得0.1升水可作为事件的区域。解:取出0.1升中“含有这个细菌”这一事件记为A,则 当堂检测1.在线段[0,3]上任取一点,则此点坐标大于1的概率是( )
A 、1/3 B 、2/3 C、1/2 D、1/3
2.在等腰直角三角形ABC中,在斜线段AB上任取一点M,则AM的长小于AC的长的概率是__________。
3.如图所示,在直角坐标系xOy内,射线OT落在120°的终边上,任作一条射线OA,则射线OA落在∠xOT内的概率为 。当堂训练4.在1L高产小麦种子中混入了一粒带麦锈病的种子,从中随机取出10mL,含有麦锈病种子的概率是多少?当堂训练5.在1万平方公里的海域中有40平方公里的大陆贮藏着石油.假如在海域中任意一点钻探,钻到油层面的概率是多少?
6.设有一个均匀的陀螺,在其圆周的一半上均匀的刻上区间[0,1]上的诸数字,另一半上均匀的刻上区间[1,3]的诸数字(所有的数字均按大小排列,且0与3重合)。旋转陀螺,求它停下时,其圆周上触及桌面的刻度为于[0.5,1.5]上的概率当堂训练7.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率。打开收音机的时刻位于[50,60]时间段内则事件A发生.由几何概型的求概率公式得
P(A)=(60-50)/60=1/6
即“等待报时的时间不超过10分钟”的概率为1/6.解:记“等待的时间小于10分钟”为事件A,8.已知地铁列车每10min一班,在车站停1min.求乘客到达站台立即乘上车的概率.9.射箭比赛的箭靶是涂有五个彩色的分环.从外向内为白色、黑色、蓝色、红色,靶心是金色,金色靶心叫“黄心”.奥运会的比赛靶面直径为122cm,靶心直径为12.2cm.运动员在70m外射箭,假设每箭都能中靶,且射中靶面内任一点都是等可能的,那么射中黄心的概率是多少?解题方法小结:对于复杂的实际问题,解题的关键是要建立概率模型,找出随机事件与所有基本事件相对应的几何区域,把问题转化为几何概型的问题,利用几何概型公式求解。
课堂小结1.几何概型适用于试验结果是无穷多且事件是等可能发生的概率类型。
2.几何概型主要用于解决长度、面积、体积有关的题目。
3.注意理解几何概型与古典概型的区别。
4.理解如何将实际问题转化为几何概型的问题,利用几何概型公式求解。
