(新人教b版必修3)数学:第一章《算法初步-单元综合》课件
文档属性
| 名称 | (新人教b版必修3)数学:第一章《算法初步-单元综合》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 58.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-14 00:00:00 | ||
图片预览









文档简介
课件40张PPT。1、算法初步目标:了解算法的基本思想;培养使用算法的思想进行思考与表达解决问题的能力。内容:
1、算法的含义。
2、程序框图。
3、实现算法的程序。
4、典型的算法介绍。 1、算法的含义算法:用计算机解决问题的某一类问题的程序或步骤,且在有限步内完成。理解:
1、算法是一种解决问题的过程和步骤。
2、算法是解决某一类问题的。
3、算法具有某种意义上的通用性和普适性。
4、算法是与计算机对话的一种思维方式。
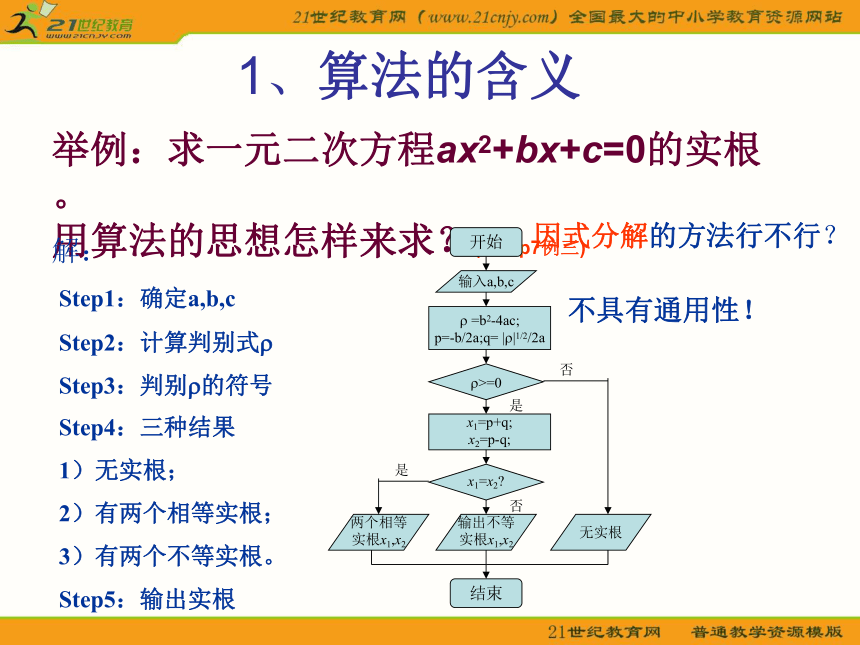
5、算法必须有限步完成。举例:求一元二次方程ax2+bx+c=0的实根。 用算法的思想怎样来求?(全解p7例三) 1、算法的含义因式分解的方法行不行?不具有通用性!解:Step1:确定a,b,c
Step2:计算判别式?
Step3:判别?的符号
Step4:三种结果
1)无实根;
2)有两个相等实根;
3)有两个不等实根。
Step5:输出实根 1、算法的含义例1 任意给定一个大于1的整数n,试设计一个算法步骤对n是否为质数做出判断。Step1:输入n,如果n=2,则n是质数;若n>2,执行第二步;
Step2:令flag=1,标记flag区分是否存在整除的情况;
Step3:依次从2~n-1循环检验是否为n的因数,在某一步,若是n的因数,则令flag=0,中途直接停止即可,并作出判断,n不是质数;
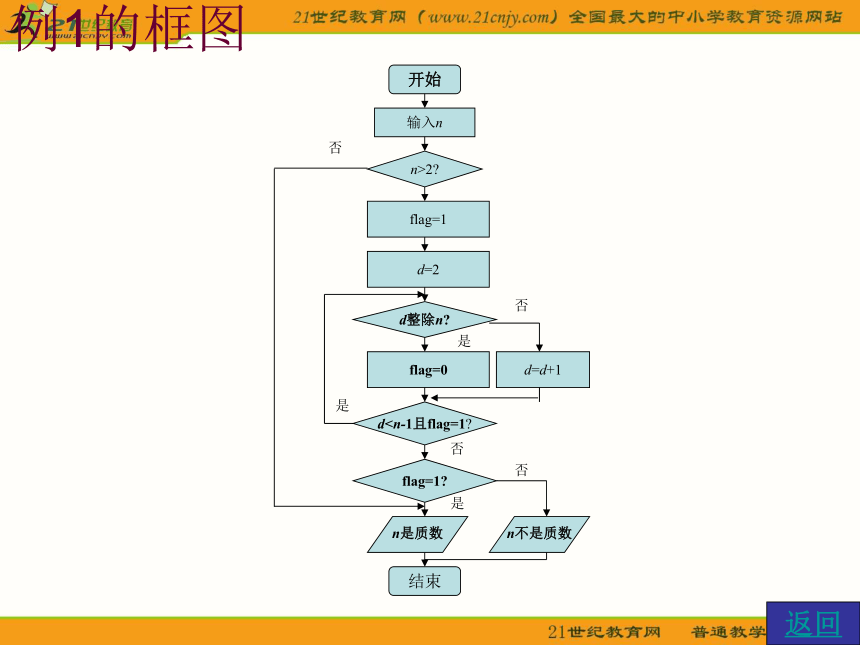
Step4:如果循环检查完2~n-1中的每一个数,flag=1仍然成立,则可以做出判断, n是质数。总体思路:如果n大于2,将n依次除以2~n-1,检查每一次是否整除,若某一次整除,则n不是质数,否则,全部检查完,仍没有整除的情况,则n是质数;n=2,直接判断是质数。 1、算法的含义例1、详细步骤:Step1:输入n,如果n=2,则n是质数,结束;若n>2,执行第二步;
Step2:令flag=1;
Step3:1)d=2;
2)d整除n ?
21)是,flag=0;
22)否,d自增加1(d=d+1);
3)d<=n-1且flag=1 ?
31)是,重新判断第2)步(即转2)步);
32)否,下一步;
Step4:flag=1 ? 41)是, n是质数;
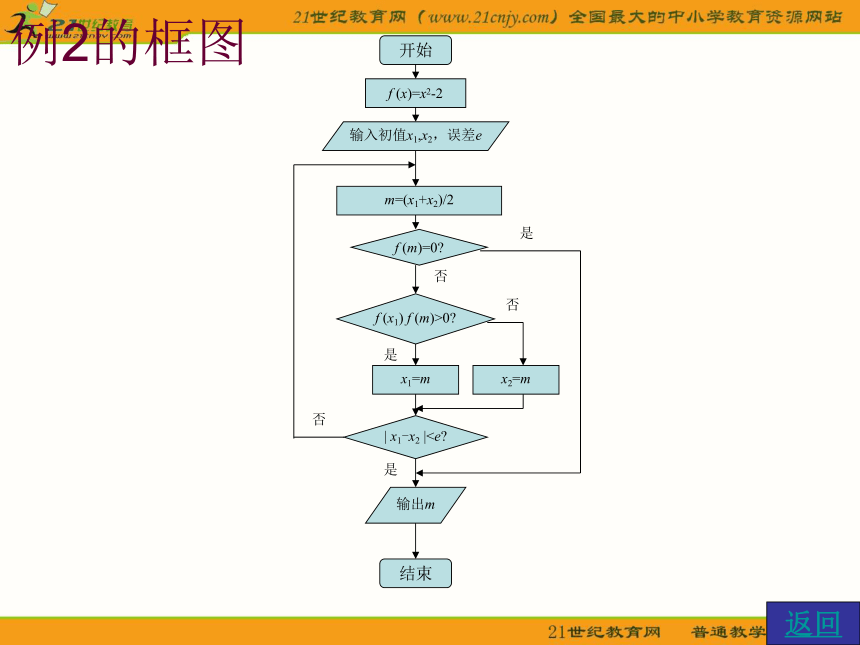
42)否, n不是质数。框图 1、算法的含义例2、 用二分法求方程x2-2=0的近似根的算法。Step1:令f (x)=x2-2,取区间端点为x1=1,x2=2,则f (x1)<0, f (x2)>0;
Step2:令m=(x1+x2)/2,判断f (m) =0 ? 若是,m即为所求,停止;
Step3:否则,判断f (x1) ·f (m) >0 ? 若成立,令x1= m ;
否则,令x2= m;
Step4:判断| x1-x2 | 若是, x1,x2之间的任意点均为满足条件的近似根;
否则,返回Step2重复进行。总体思路:设定一个区间,包含方程的根,每次取区间的中点,改变原区间的一个端点,以缩小区间,但始终保持该区间包含方程的根,最后使区间缩小到非常小的程度,达到近似根的精度要求,则区间内任意点都可以作为方程的根。框图 1、算法的含义f(x)=x2-2x2=2x1=11.51.251.375 1、算法的含义小结:算法是“傻瓜式”的,即算法要“面面俱到”,不能省略任何一个细小的步骤,只有这样,才能在设计出算法后,把具体的执行过程交给计算机完成。
但,算法有“好”与“不好” 之分,“好”的算法可以节约计算机的执行时间,“不好” 的算法占用大量的计算机时间。 1、算法的含义例如:枚举法。
x1,x2,x3,x4,x5为0-999之间的整数,求满足x1+x2+x3+x4+x5=2050的条件下,乘积 x1·x2·x3·x4·x5 达到最大。
解:计算机枚举出所有可能的组合
(1000)5=1015,现有计算机计算约为200多年。
而实际上,可以找到算法算出,当x1=x2=x3=x4=x5=410时,x1·x2·x3·x4·x5 达到最大。 2、程序框图框图:又称流程图,是表达算法的重要工具,借助框图,人们可以清晰而条理地表达思想。理解:
1、框图的表现形式:程序框和流程线的组合形式。
2、程序框和流程线是一种形式规范,好的形式规范,是交流重要前提。
3、通过框图将解题思想表达为计算机的“思维”习惯。例1的框图返回例2的框图返回 2、程序框图通过框图,算法的逻辑结构表现得非常清楚,通常有三种结构:
1.顺序结构;
2.条件(选择)结构;
3.循环结构。 2、程序框图(1)顺序结构
例3:已知三角形的三边边长为2,3,4,计算面积。思路:
1、秦九韶面积公式:S=[p(p-a)(p-b)(p-c)]1/2
2、其中,p=(a+b+c)/2解决:
1、输入边长a,b,c,计算p的值。
2、按公式计算S,输出S。 2、程序框图解: 2、程序框图(2)条件结构
例4:任意给定3个正实数,判断分别以这些实数为边长的三角形是否存在。思路:
1、条件:a+b>c且a+c>b且b+c>a
2、条件成立,存在该三角形,否则,不存在。解决:
1、输入边长a,b,c,判断思路1中的条件。
2、根据思路2中的结论,输出结论。 2、程序框图解: 2、程序框图(3)循环结构
例5:设计一个计算1+2+…+100的值的算法。思路:
1、算法要实现累加:问题是一个连加,按照算法的通用性和普适性来说,该问题的共性是加法,且重复。
2、有限次完成。解决:
1、设置一个累加变量,用于存放总和。
2、设置一个计数变量,用于判断累加次数是否超过100次。 2、程序框图解:直到型当型习题: 1、设计一个求12+22+…+1002的值。(思考)2、某居民区的物业部门每月向居民收取卫生费:3人和3人以下的住户,每月收取5元,超过3人的住户,每超过1人加收1.2元.设计算法,根据输入的人数,计算应收取的卫生费,画出框图。(思考)解答: 1、略。2、分析:卫生费是一个分段函数: 3、实现算法的程序计算机要完成任何一项任务都需要算法,但要让计算机正确执行,必须要将算法“翻译”成计算机能够读懂的程序才能执行。高级语言包括:BASIC,PASCAL,C,
C++(Visual C++,Bland C++等),JAVA,Power Builder,
Delphi等,只要掌握一门或两门高级语言即可。 3、实现算法的程序例1、用描点法作函数
的图像时,要求出自变量和函数的一组对应值,编写程序,分别计算当x=-5,-4,-3,-2,-1,0,1,2,3,4,5时的函数值. 3、实现算法的程序例2、计算一个学生的数学、语文、英语三门课的平均成绩.例3、给一个变量重复赋值.例4、交换两个变量A和B的值,并输出交换前后的值. 3、实现算法的程序例5、编写程序求ax2+bx+c=0方程的根.例6、编写程序,使任意输入的3个数从大到小的顺序输出.习题:判断一年是否为闰年的程序. 3、实现算法的程序循环结构:编写求和程序.编写判断是否是质数的程序.思考:改进判断质数的程序.习题:二分法求x2-2=0的近似根.案例1:辗转法相除求两数最大公约数求8251与6105的最大公约数8251=6105 ?1 +21466105=2?2146+18132146=1813 ?1 +3331813= 5 ? 333+148333 = 2? 148+37148 = 4? 37+0 4、典型的算法介绍程序流程图更相减损术可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等着,以等数约之。第1步:任给两个正整数;判断它们是否是偶数,若是,用2约简;若不是,执行第2步。
第2步:以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数,继续这个操作直到所得的数相等为止。例1 更相减损术求98与63的最大公约数案例2:秦九韶算法f(x)=x5+x4+x3+x2+x+1(需做10次乘法,5次加法)
=x*x*x*x*x+x*x*x*x+x*x*x+x*x+x
=(((( x?x+x) ?x+x) ?x+x) ?x+x+1) (4次乘法,5次加法)f(x)=anxn+ an-1xn-1 + … a1x +a0 =(…(((anx+ an-1)x+ … +a1) x+a0 =(anxn-1+ an-1xn-2 + … a1 ) x +a0 =((anxn-2+ an-1xn-3 + … +a2) x + a1 ) x +a0 =…v1=5?5+2=27
v2=27 ?5 +3.5=138.5
v3=138.5 ?5-2.6=689.9
v4=689.9 ?5+1.7=3451.2
v5=3451.2 ?5-0.8=17255.2 例2 :已知一个5次多项式为 f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8思考:总计多少次乘,多少次加?f(x)=anxn+ an-1xn-1 + … a1x +a0 =(…(((anx+ an-1)x+ … +a1) x+a0程序流程图案例3:排序i 0 1 2 3 4 5 6 7 8
{(49),38,65,97,76,13,27,49}
2 (38) {(38,49),65,97,76,13,27,49}
3 {(38,49,65),97,76,13,27,49}
4 {(38,49,65,97),76,13,27,49}
5 (76) {(38,49,65,76,97),13,27,49}
6 (13) {(13,38,49,65,76,97),27,49}
7 (27) {(13,27,38,49,65,76,97),49}
8 (49) {(13,27,38,49,49,65,76,97)}实例数据1: (49),38,65,97,76,13,27,49直接插入排序i 0 1 2 3 4 5 6
{(8),3, 2, 5, 9, 6 }
2 (3) {(3, 8), 2, 5, 9, 6 }
3 (2) {(2, 3, 8), 5, 9, 6 }
4 (5) { (2, 3, 5, 8),9, 6 }
5 (9) { (2, 3, 5, 8 , 9 ),6} 6 (6) { (2, 3, 5 ,6 , 8 , 9)}实例数据2: 8,3,2,5,9,6例3 用冒泡法对数据7,5,3,9,1从小到大进行排序7
5
3
9
15
7
3
9
15
3
7
9
15
3
7
9
11
3
5
7
9见程序paixu2.bas案例4:进位制进位制是人们为了计数和运算方便而约定的计数系统,“满几进一” 就是几进制。几进制的基数就是几。3721=3?103+ 7?102+ 2?101+ 1?100一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式
an an -1… a1 a0(k)(0 =1?32+ 1?16+ 1?2 + 1
=51 例5 把89二进制数89=2 ?44+1
44=2 ?22+0
22=2 ?11+089=2 ?(2 ?(2 ?(2 ? (2 ? 2 + 1) + 1)+0)+0)+1
=1?26+ 0?25+ 1?24 + 1?23 + 0?22 + 0?21 + 1?2011=2 ? 5 + 1
5=2 ? 2 + 1除2取余法余数89=(1011001)2例6 把89五进制数89=(324)5 思考 割圆术循环结构:编写求和程序.设圆的半径为1,弦心距为hn ,边长为xn,面积为Sn,由勾股定理hnxnx2n
1、算法的含义。
2、程序框图。
3、实现算法的程序。
4、典型的算法介绍。 1、算法的含义算法:用计算机解决问题的某一类问题的程序或步骤,且在有限步内完成。理解:
1、算法是一种解决问题的过程和步骤。
2、算法是解决某一类问题的。
3、算法具有某种意义上的通用性和普适性。
4、算法是与计算机对话的一种思维方式。
5、算法必须有限步完成。举例:求一元二次方程ax2+bx+c=0的实根。 用算法的思想怎样来求?(全解p7例三) 1、算法的含义因式分解的方法行不行?不具有通用性!解:Step1:确定a,b,c
Step2:计算判别式?
Step3:判别?的符号
Step4:三种结果
1)无实根;
2)有两个相等实根;
3)有两个不等实根。
Step5:输出实根 1、算法的含义例1 任意给定一个大于1的整数n,试设计一个算法步骤对n是否为质数做出判断。Step1:输入n,如果n=2,则n是质数;若n>2,执行第二步;
Step2:令flag=1,标记flag区分是否存在整除的情况;
Step3:依次从2~n-1循环检验是否为n的因数,在某一步,若是n的因数,则令flag=0,中途直接停止即可,并作出判断,n不是质数;
Step4:如果循环检查完2~n-1中的每一个数,flag=1仍然成立,则可以做出判断, n是质数。总体思路:如果n大于2,将n依次除以2~n-1,检查每一次是否整除,若某一次整除,则n不是质数,否则,全部检查完,仍没有整除的情况,则n是质数;n=2,直接判断是质数。 1、算法的含义例1、详细步骤:Step1:输入n,如果n=2,则n是质数,结束;若n>2,执行第二步;
Step2:令flag=1;
Step3:1)d=2;
2)d整除n ?
21)是,flag=0;
22)否,d自增加1(d=d+1);
3)d<=n-1且flag=1 ?
31)是,重新判断第2)步(即转2)步);
32)否,下一步;
Step4:flag=1 ? 41)是, n是质数;
42)否, n不是质数。框图 1、算法的含义例2、 用二分法求方程x2-2=0的近似根的算法。Step1:令f (x)=x2-2,取区间端点为x1=1,x2=2,则f (x1)<0, f (x2)>0;
Step2:令m=(x1+x2)/2,判断f (m) =0 ? 若是,m即为所求,停止;
Step3:否则,判断f (x1) ·f (m) >0 ? 若成立,令x1= m ;
否则,令x2= m;
Step4:判断| x1-x2 |
否则,返回Step2重复进行。总体思路:设定一个区间,包含方程的根,每次取区间的中点,改变原区间的一个端点,以缩小区间,但始终保持该区间包含方程的根,最后使区间缩小到非常小的程度,达到近似根的精度要求,则区间内任意点都可以作为方程的根。框图 1、算法的含义f(x)=x2-2x2=2x1=11.51.251.375 1、算法的含义小结:算法是“傻瓜式”的,即算法要“面面俱到”,不能省略任何一个细小的步骤,只有这样,才能在设计出算法后,把具体的执行过程交给计算机完成。
但,算法有“好”与“不好” 之分,“好”的算法可以节约计算机的执行时间,“不好” 的算法占用大量的计算机时间。 1、算法的含义例如:枚举法。
x1,x2,x3,x4,x5为0-999之间的整数,求满足x1+x2+x3+x4+x5=2050的条件下,乘积 x1·x2·x3·x4·x5 达到最大。
解:计算机枚举出所有可能的组合
(1000)5=1015,现有计算机计算约为200多年。
而实际上,可以找到算法算出,当x1=x2=x3=x4=x5=410时,x1·x2·x3·x4·x5 达到最大。 2、程序框图框图:又称流程图,是表达算法的重要工具,借助框图,人们可以清晰而条理地表达思想。理解:
1、框图的表现形式:程序框和流程线的组合形式。
2、程序框和流程线是一种形式规范,好的形式规范,是交流重要前提。
3、通过框图将解题思想表达为计算机的“思维”习惯。例1的框图返回例2的框图返回 2、程序框图通过框图,算法的逻辑结构表现得非常清楚,通常有三种结构:
1.顺序结构;
2.条件(选择)结构;
3.循环结构。 2、程序框图(1)顺序结构
例3:已知三角形的三边边长为2,3,4,计算面积。思路:
1、秦九韶面积公式:S=[p(p-a)(p-b)(p-c)]1/2
2、其中,p=(a+b+c)/2解决:
1、输入边长a,b,c,计算p的值。
2、按公式计算S,输出S。 2、程序框图解: 2、程序框图(2)条件结构
例4:任意给定3个正实数,判断分别以这些实数为边长的三角形是否存在。思路:
1、条件:a+b>c且a+c>b且b+c>a
2、条件成立,存在该三角形,否则,不存在。解决:
1、输入边长a,b,c,判断思路1中的条件。
2、根据思路2中的结论,输出结论。 2、程序框图解: 2、程序框图(3)循环结构
例5:设计一个计算1+2+…+100的值的算法。思路:
1、算法要实现累加:问题是一个连加,按照算法的通用性和普适性来说,该问题的共性是加法,且重复。
2、有限次完成。解决:
1、设置一个累加变量,用于存放总和。
2、设置一个计数变量,用于判断累加次数是否超过100次。 2、程序框图解:直到型当型习题: 1、设计一个求12+22+…+1002的值。(思考)2、某居民区的物业部门每月向居民收取卫生费:3人和3人以下的住户,每月收取5元,超过3人的住户,每超过1人加收1.2元.设计算法,根据输入的人数,计算应收取的卫生费,画出框图。(思考)解答: 1、略。2、分析:卫生费是一个分段函数: 3、实现算法的程序计算机要完成任何一项任务都需要算法,但要让计算机正确执行,必须要将算法“翻译”成计算机能够读懂的程序才能执行。高级语言包括:BASIC,PASCAL,C,
C++(Visual C++,Bland C++等),JAVA,Power Builder,
Delphi等,只要掌握一门或两门高级语言即可。 3、实现算法的程序例1、用描点法作函数
的图像时,要求出自变量和函数的一组对应值,编写程序,分别计算当x=-5,-4,-3,-2,-1,0,1,2,3,4,5时的函数值. 3、实现算法的程序例2、计算一个学生的数学、语文、英语三门课的平均成绩.例3、给一个变量重复赋值.例4、交换两个变量A和B的值,并输出交换前后的值. 3、实现算法的程序例5、编写程序求ax2+bx+c=0方程的根.例6、编写程序,使任意输入的3个数从大到小的顺序输出.习题:判断一年是否为闰年的程序. 3、实现算法的程序循环结构:编写求和程序.编写判断是否是质数的程序.思考:改进判断质数的程序.习题:二分法求x2-2=0的近似根.案例1:辗转法相除求两数最大公约数求8251与6105的最大公约数8251=6105 ?1 +21466105=2?2146+18132146=1813 ?1 +3331813= 5 ? 333+148333 = 2? 148+37148 = 4? 37+0 4、典型的算法介绍程序流程图更相减损术可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等着,以等数约之。第1步:任给两个正整数;判断它们是否是偶数,若是,用2约简;若不是,执行第2步。
第2步:以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数,继续这个操作直到所得的数相等为止。例1 更相减损术求98与63的最大公约数案例2:秦九韶算法f(x)=x5+x4+x3+x2+x+1(需做10次乘法,5次加法)
=x*x*x*x*x+x*x*x*x+x*x*x+x*x+x
=(((( x?x+x) ?x+x) ?x+x) ?x+x+1) (4次乘法,5次加法)f(x)=anxn+ an-1xn-1 + … a1x +a0 =(…(((anx+ an-1)x+ … +a1) x+a0 =(anxn-1+ an-1xn-2 + … a1 ) x +a0 =((anxn-2+ an-1xn-3 + … +a2) x + a1 ) x +a0 =…v1=5?5+2=27
v2=27 ?5 +3.5=138.5
v3=138.5 ?5-2.6=689.9
v4=689.9 ?5+1.7=3451.2
v5=3451.2 ?5-0.8=17255.2 例2 :已知一个5次多项式为 f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8思考:总计多少次乘,多少次加?f(x)=anxn+ an-1xn-1 + … a1x +a0 =(…(((anx+ an-1)x+ … +a1) x+a0程序流程图案例3:排序i 0 1 2 3 4 5 6 7 8
{(49),38,65,97,76,13,27,49}
2 (38) {(38,49),65,97,76,13,27,49}
3 {(38,49,65),97,76,13,27,49}
4 {(38,49,65,97),76,13,27,49}
5 (76) {(38,49,65,76,97),13,27,49}
6 (13) {(13,38,49,65,76,97),27,49}
7 (27) {(13,27,38,49,65,76,97),49}
8 (49) {(13,27,38,49,49,65,76,97)}实例数据1: (49),38,65,97,76,13,27,49直接插入排序i 0 1 2 3 4 5 6
{(8),3, 2, 5, 9, 6 }
2 (3) {(3, 8), 2, 5, 9, 6 }
3 (2) {(2, 3, 8), 5, 9, 6 }
4 (5) { (2, 3, 5, 8),9, 6 }
5 (9) { (2, 3, 5, 8 , 9 ),6} 6 (6) { (2, 3, 5 ,6 , 8 , 9)}实例数据2: 8,3,2,5,9,6例3 用冒泡法对数据7,5,3,9,1从小到大进行排序7
5
3
9
15
7
3
9
15
3
7
9
15
3
7
9
11
3
5
7
9见程序paixu2.bas案例4:进位制进位制是人们为了计数和运算方便而约定的计数系统,“满几进一” 就是几进制。几进制的基数就是几。3721=3?103+ 7?102+ 2?101+ 1?100一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式
an an -1… a1 a0(k)(0
=51 例5 把89二进制数89=2 ?44+1
44=2 ?22+0
22=2 ?11+089=2 ?(2 ?(2 ?(2 ? (2 ? 2 + 1) + 1)+0)+0)+1
=1?26+ 0?25+ 1?24 + 1?23 + 0?22 + 0?21 + 1?2011=2 ? 5 + 1
5=2 ? 2 + 1除2取余法余数89=(1011001)2例6 把89五进制数89=(324)5 思考 割圆术循环结构:编写求和程序.设圆的半径为1,弦心距为hn ,边长为xn,面积为Sn,由勾股定理hnxnx2n
