位似(一)
图片预览

文档简介
课题 27.3 位似(一)(学生用)
(新授课)
【学习目标】
1.了解位似图形和位似中心的概念;了解位似与相似的联系和区别,会利用
位似的性质将一个图形放大或缩小.
2.能利用图形的位似解决一些简单的实际问题,发展数学应用意识,发展初步的演绎推理能力.
3.在探索图形的性质、图形的变换以及平面图形与空间几何体的相互转换等活动过程中,初步建立空间观念,发展几何直觉.
【教学重难点】
1. 重点:位似图形的概念,位似图形的性质.
2. 难点:位似图形性质的理解和逆向应用.
课前延伸
【知识梳理】
(1) 我们已经学过的图形变换有 变换、 变换、 变换.
(2) 图形的旋转是由 和 两大要素决定的, 在旋转过程中保持不动,图形旋转后, 和 都没有变化.
(3) 下列说法正确的是( )
A.能重合的两个图形成中心对称 B.成中心对称的两个图形必能完全重合
C.平移后能重合的两个图形成中心对称 D.旋转对称图形就是中心对称图形
(4) 如图,四边形CDEF旋转后能与正方形ABCD重合,那么图形所在平面上可作旋转中心的点有 个.
二、预习思考题及答案
(1)你了解放映电影时屏幕上的图形是怎样得到的吗?
(2)给你一个三角形,你能将它按比例放大(或缩小)吗?
自主学习记录卡
1.自学本课内容后,你有哪些疑难之处?2.你有哪些问题要提交小组讨论?
课内探究
一、课堂探究1(问题探究,自主学习)
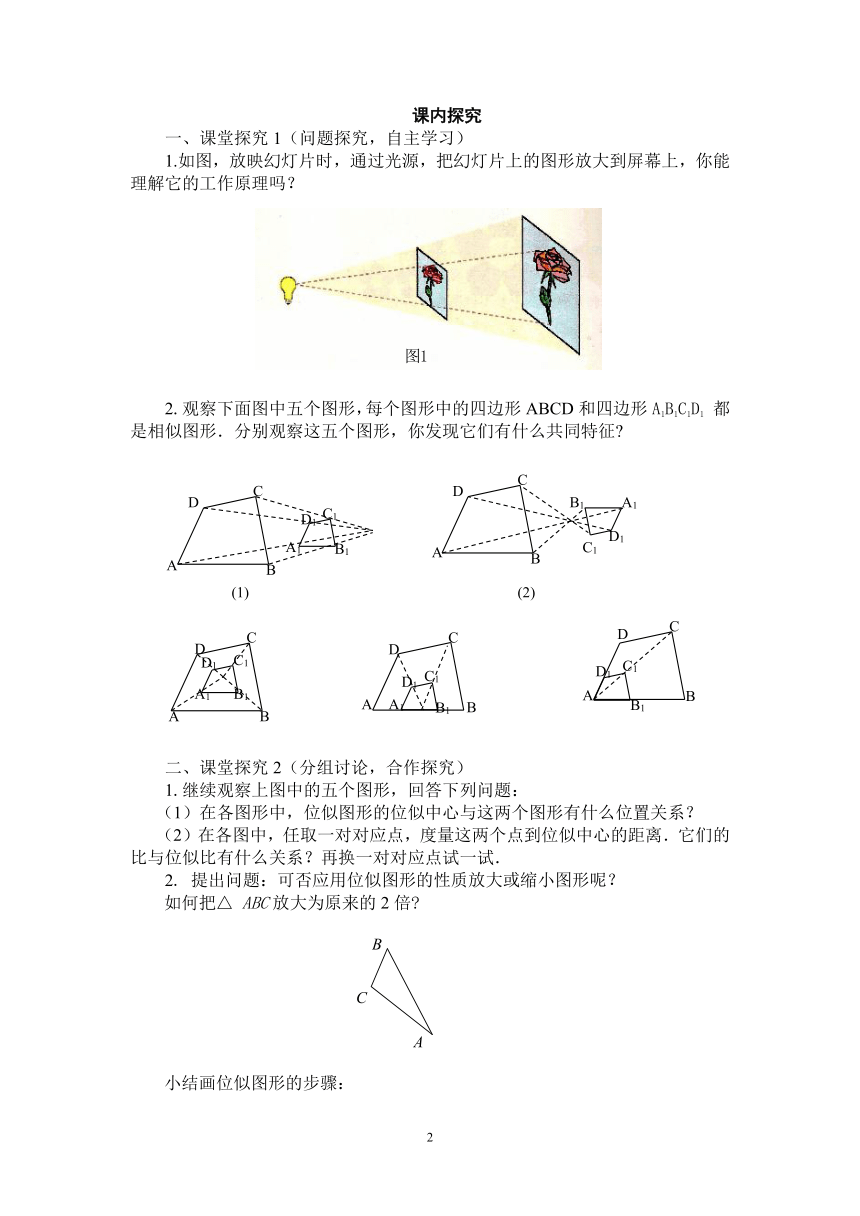
1.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上,你能理解它的工作原理吗?
2.观察下面图中五个图形,每个图形中的四边形ABCD和四边形A1B1C1D1 都是相似图形.分别观察这五个图形,你发现它们有什么共同特征
二、课堂探究2(分组讨论,合作探究)
1.继续观察上图中的五个图形,回答下列问题:
(1)在各图形中,位似图形的位似中心与这两个图形有什么位置关系?
(2)在各图中,任取一对对应点,度量这两个点到位似中心的距离.它们的比与位似比有什么关系?再换一对对应点试一试.
2. 提出问题:可否应用位似图形的性质放大或缩小图形呢?
如何把△ ABC放大为原来的2倍
小结画位似图形的步骤:
三、反馈训练(可以设计成必做题与选做题两类,分层要求)
1.如图,D,E分别是AB,AC上的点.
(1)如果DE∥BC,那么△ADE和△ABC位似图形吗 为什么
(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗 为什么
2.下面每组图形中都有两个图形.
(1)哪一组中的每两个图形是位似图形
(2)作出位似图形的位似中心
2.如图AB,CD相交于点E,AC∥DB. △ACE与△BDE是位似图形吗?为什么?
课后提升
1.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的是格点三角形.在建立平面直角坐标系后,点的坐标为.
(1)把向左平移8格后得到,画出的图形并写出点的坐标;
(2)把绕点按顺时针方向旋转后得到,画出的图形并写出点的坐标;
(3)把以点为位似中心放大,使放大前后对应边长的比为1:2,画出的图形.
2.阅读并解答问题.
在给定的锐角△ABC中,求作一个正方形DEFG,使D、E落在BC上,F、G分别落在AC、AB边上,作法如下:
第一步:画一个有3个顶点落在△ABC两边上的正方形D'E'F'G'.
第二步:连结BF',并延长交AC于点F;
第三步:过F点作FE⊥BC于E;
第四步:过F点作FG∥BC交AB于点G;
第五步:过G点作GD⊥BC于点D.
四边形DEFG即为所求作的四边形DEFG为正方形.
问题:
(1)证明上述所求作的四边形DEFG为正方形;
(2)在△ABC中,如果,∠BAC=75°,求上述正方形DEFG的边长.
y
x
B1
D
C
B
A
E
B
D
A
C
(6)
(5)
(4)
(3)
(2)
(1)
(2)
(1)
B1
D1
A1
C1
D
C
B
A
D1
C1
B1
A1
D
C
B
A
D
C
B
A
D1
C1
B1
A1
D
C
B
A
D1
C1
B1
D1
C1
A1
O
A
B
C
PAGE
4
(新授课)
【学习目标】
1.了解位似图形和位似中心的概念;了解位似与相似的联系和区别,会利用
位似的性质将一个图形放大或缩小.
2.能利用图形的位似解决一些简单的实际问题,发展数学应用意识,发展初步的演绎推理能力.
3.在探索图形的性质、图形的变换以及平面图形与空间几何体的相互转换等活动过程中,初步建立空间观念,发展几何直觉.
【教学重难点】
1. 重点:位似图形的概念,位似图形的性质.
2. 难点:位似图形性质的理解和逆向应用.
课前延伸
【知识梳理】
(1) 我们已经学过的图形变换有 变换、 变换、 变换.
(2) 图形的旋转是由 和 两大要素决定的, 在旋转过程中保持不动,图形旋转后, 和 都没有变化.
(3) 下列说法正确的是( )
A.能重合的两个图形成中心对称 B.成中心对称的两个图形必能完全重合
C.平移后能重合的两个图形成中心对称 D.旋转对称图形就是中心对称图形
(4) 如图,四边形CDEF旋转后能与正方形ABCD重合,那么图形所在平面上可作旋转中心的点有 个.
二、预习思考题及答案
(1)你了解放映电影时屏幕上的图形是怎样得到的吗?
(2)给你一个三角形,你能将它按比例放大(或缩小)吗?
自主学习记录卡
1.自学本课内容后,你有哪些疑难之处?2.你有哪些问题要提交小组讨论?
课内探究
一、课堂探究1(问题探究,自主学习)
1.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上,你能理解它的工作原理吗?
2.观察下面图中五个图形,每个图形中的四边形ABCD和四边形A1B1C1D1 都是相似图形.分别观察这五个图形,你发现它们有什么共同特征
二、课堂探究2(分组讨论,合作探究)
1.继续观察上图中的五个图形,回答下列问题:
(1)在各图形中,位似图形的位似中心与这两个图形有什么位置关系?
(2)在各图中,任取一对对应点,度量这两个点到位似中心的距离.它们的比与位似比有什么关系?再换一对对应点试一试.
2. 提出问题:可否应用位似图形的性质放大或缩小图形呢?
如何把△ ABC放大为原来的2倍
小结画位似图形的步骤:
三、反馈训练(可以设计成必做题与选做题两类,分层要求)
1.如图,D,E分别是AB,AC上的点.
(1)如果DE∥BC,那么△ADE和△ABC位似图形吗 为什么
(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗 为什么
2.下面每组图形中都有两个图形.
(1)哪一组中的每两个图形是位似图形
(2)作出位似图形的位似中心
2.如图AB,CD相交于点E,AC∥DB. △ACE与△BDE是位似图形吗?为什么?
课后提升
1.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的是格点三角形.在建立平面直角坐标系后,点的坐标为.
(1)把向左平移8格后得到,画出的图形并写出点的坐标;
(2)把绕点按顺时针方向旋转后得到,画出的图形并写出点的坐标;
(3)把以点为位似中心放大,使放大前后对应边长的比为1:2,画出的图形.
2.阅读并解答问题.
在给定的锐角△ABC中,求作一个正方形DEFG,使D、E落在BC上,F、G分别落在AC、AB边上,作法如下:
第一步:画一个有3个顶点落在△ABC两边上的正方形D'E'F'G'.
第二步:连结BF',并延长交AC于点F;
第三步:过F点作FE⊥BC于E;
第四步:过F点作FG∥BC交AB于点G;
第五步:过G点作GD⊥BC于点D.
四边形DEFG即为所求作的四边形DEFG为正方形.
问题:
(1)证明上述所求作的四边形DEFG为正方形;
(2)在△ABC中,如果,∠BAC=75°,求上述正方形DEFG的边长.
y
x
B1
D
C
B
A
E
B
D
A
C
(6)
(5)
(4)
(3)
(2)
(1)
(2)
(1)
B1
D1
A1
C1
D
C
B
A
D1
C1
B1
A1
D
C
B
A
D
C
B
A
D1
C1
B1
A1
D
C
B
A
D1
C1
B1
D1
C1
A1
O
A
B
C
PAGE
4
