(北师大版必修3)数学:模拟方法-概率的应用 课件
文档属性
| 名称 | (北师大版必修3)数学:模拟方法-概率的应用 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 36.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-14 00:00:00 | ||
图片预览





文档简介
课件17张PPT。模拟方法--
概率的应用问题:房间的纱窗破了一个小洞,随机向纱窗投一粒小石子,估计小石子从小洞穿过的概率。 试验1:
取一个矩形,在面积为四分之一的部分画上阴影,随机地向矩形中撒一把豆子(我们数100粒),统计落在阴影内的豆子数与落在矩形内的总豆子数,观察它们有怎样的比例关系? 结论:试验2:
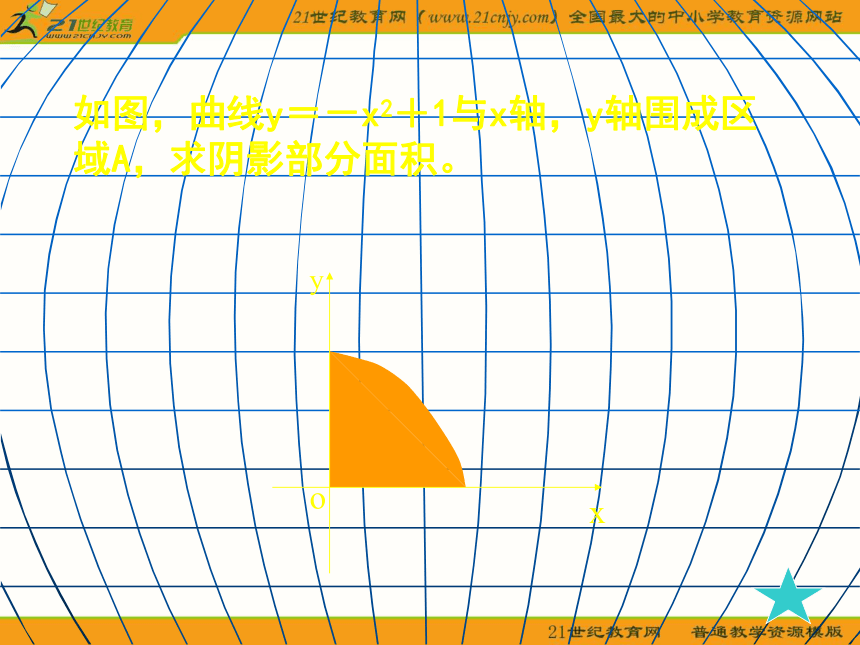
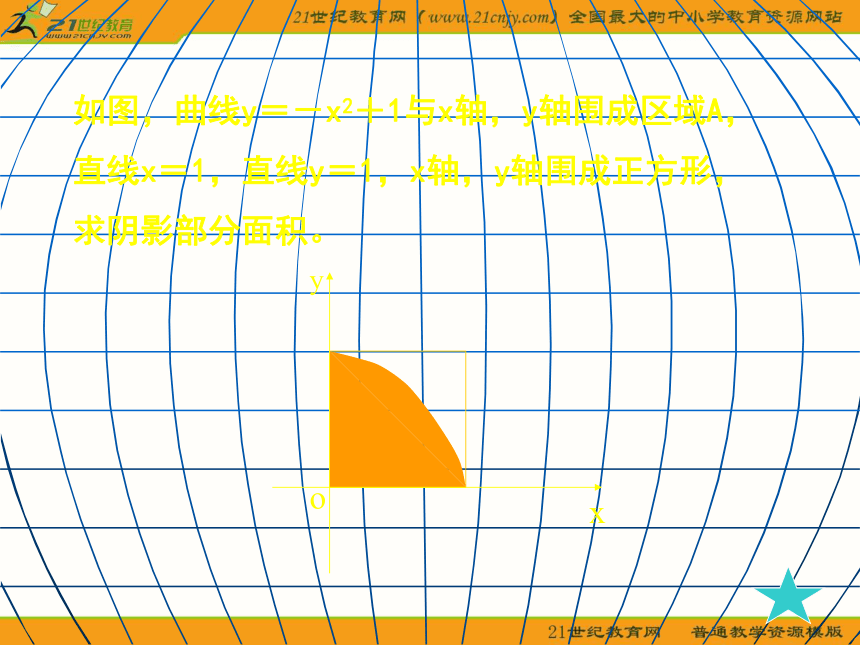
取一个矩形,随机地向矩形中撒一把豆子,统计落在阴影内的豆子数与落在矩形内的总豆子数,你能根据豆子数得到什么结论? 如图,曲线y=-x2+1与x轴,y轴围成区域A,求阴影部分面积。xyo如图,曲线y=-x2+1与x轴,y轴围成区域A,
直线x=1,直线y=1,x轴,y轴围成正方形,
求阴影部分面积。我国古代数学家祖冲之早在1500多年前就算出圆周率π的值在3.1415926和3.1415927之间,这是我国古代数学家的一大成就,利用模拟方法,我们也可以对圆周率π的值作出估计。你能设计一个方案来模拟吗? 如果在正方形中撒了n颗豆子,其中有m颗豆子落在圆中,则圆周率π的近似值是多少? 如果正方形面积不变,但形状改变,所得的比例发生变化吗?每个事件发生的概率只与该事件区域的长度(面积或体积)成比例。即:
P(点落在阴影区域)= 几何概型的特点:(1)试验结果有无限多个(2)每个试验结果的发生是等可能的几何概型的概率公式: P(A)= 例1、如图,在墙上挂着一块边长为16cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm、4cm、6cm,某人站在3m处向此板投镖,设投镖击中线上或没有投中木板时都不算,可重投。 问:(1)投中大圆内的概率是多少? (2)投中小圆和中圆形成的 圆环的概率是多少? (3)投中大圆之外 的概率是多少? 例2、小明家的晚报在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐。
(1)你认为晚报在晚餐开始之前被送到和在晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少? 我们用模拟方法来估计晚报在晚餐开始之前被送到的概率:
用两个转盘来模拟上述过程,一个转盘
用于模拟晚报的送达,另一个转盘用于模拟晚餐,两个转盘各转动一次并记录下结果就完成一次模拟。 O在平面上如图所示建立坐标系,图中直线x=6,x=7,y=5.5,y=6.5围成一个正方形区域,设晚餐在x时开始,晚报在y时被送到,小结:
1、模拟方法的基本思想
2、用模拟方法计算不规则图形的面积
3、用模拟方法估计随机事件的概率
4、几何概型事件A发生概率的计算方法 P(A)=
概率的应用问题:房间的纱窗破了一个小洞,随机向纱窗投一粒小石子,估计小石子从小洞穿过的概率。 试验1:
取一个矩形,在面积为四分之一的部分画上阴影,随机地向矩形中撒一把豆子(我们数100粒),统计落在阴影内的豆子数与落在矩形内的总豆子数,观察它们有怎样的比例关系? 结论:试验2:
取一个矩形,随机地向矩形中撒一把豆子,统计落在阴影内的豆子数与落在矩形内的总豆子数,你能根据豆子数得到什么结论? 如图,曲线y=-x2+1与x轴,y轴围成区域A,求阴影部分面积。xyo如图,曲线y=-x2+1与x轴,y轴围成区域A,
直线x=1,直线y=1,x轴,y轴围成正方形,
求阴影部分面积。我国古代数学家祖冲之早在1500多年前就算出圆周率π的值在3.1415926和3.1415927之间,这是我国古代数学家的一大成就,利用模拟方法,我们也可以对圆周率π的值作出估计。你能设计一个方案来模拟吗? 如果在正方形中撒了n颗豆子,其中有m颗豆子落在圆中,则圆周率π的近似值是多少? 如果正方形面积不变,但形状改变,所得的比例发生变化吗?每个事件发生的概率只与该事件区域的长度(面积或体积)成比例。即:
P(点落在阴影区域)= 几何概型的特点:(1)试验结果有无限多个(2)每个试验结果的发生是等可能的几何概型的概率公式: P(A)= 例1、如图,在墙上挂着一块边长为16cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm、4cm、6cm,某人站在3m处向此板投镖,设投镖击中线上或没有投中木板时都不算,可重投。 问:(1)投中大圆内的概率是多少? (2)投中小圆和中圆形成的 圆环的概率是多少? (3)投中大圆之外 的概率是多少? 例2、小明家的晚报在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐。
(1)你认为晚报在晚餐开始之前被送到和在晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少? 我们用模拟方法来估计晚报在晚餐开始之前被送到的概率:
用两个转盘来模拟上述过程,一个转盘
用于模拟晚报的送达,另一个转盘用于模拟晚餐,两个转盘各转动一次并记录下结果就完成一次模拟。 O在平面上如图所示建立坐标系,图中直线x=6,x=7,y=5.5,y=6.5围成一个正方形区域,设晚餐在x时开始,晚报在y时被送到,小结:
1、模拟方法的基本思想
2、用模拟方法计算不规则图形的面积
3、用模拟方法估计随机事件的概率
4、几何概型事件A发生概率的计算方法 P(A)=
