(北师大版必修3)数学:第二章 算法初步(章综合)
文档属性
| 名称 | (北师大版必修3)数学:第二章 算法初步(章综合) |  | |
| 格式 | rar | ||
| 文件大小 | 62.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-15 08:43:00 | ||
图片预览






文档简介
课件15张PPT。算法初 步第一章 算法初步1.1.1算法的概念 回顾二元一次方程组
x-2y=-1 (1 )
2x+y=1 (2 )
的求解过程,我们可以归纳出以下步骤:
第一步: (2 )-(1 )×2,得 5y=3;
第二步: 解 ( 3 ) 得y=3/5;
第三步: 将y=3/5代入 ( 1) ,得x=1/5.算法这个词出现于12世纪,指的是用阿拉伯数字进行算术运算的过程。在数学中,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成。按照这样的理解,我们可以设计出很多数学问题的算法。下面看几个例子。例 1 任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定。
算法分析:根据质数的定义,很容易设计出下面的步骤:第一步:判断n是否等于2,若n=2,则n是质数;若n>2,则执行第二步。
第二步:依次从2~(n-1)检验是不是n的因数,即整除n的数。若有这样的数,则n不是质数;若没有这样的数,则n是质数。点评:这是判断一个大于1的整数n是否为质数的最基本的方法例1的程序框图例2 用二分法设计一个求方程x2-2=0的近似根的算法。算法分析:回顾二分法解方程的过程,并假设所求近似根与精确解的差的绝对值不超过0.005,则不难设计出以下步骤:第一步:令 f(x)= x2-2.因为f(1)<0,f(2)>0,所以设x1=1,x2=2.
第二步:令 ,判断f(m)是否为0,若是,则m为所求;若否,则继续判断f(x1) · f(m)大于0还是小于0。
第三步:若f(x1) · f(m)>0,则令x1= m;否则,令x2= m。
第四步:判断 <0.005是否成立?若是,则x1、 x2之间的任意取值均为满足条件的 近似根;若否,则返回第二步。
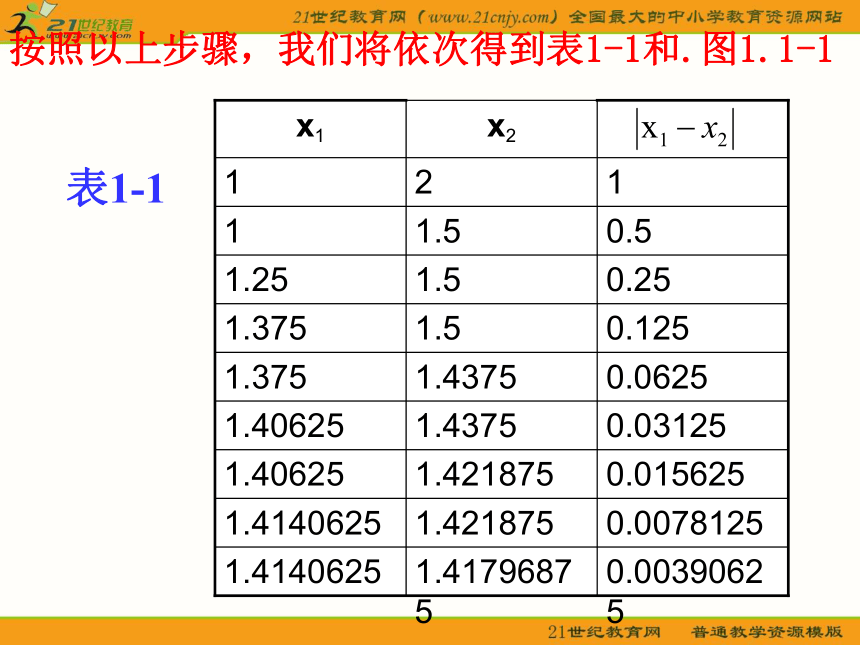
按照以上步骤,我们将依次得到表1-1和.图1.1-1表1-1
图1.1-1实际上,上述步骤就是在求 的近似值。计算机解决任何问题都要依赖于算法,只有将解决问题的过程分解为若干个明确的步骤,即算法,并用计算机能够接受的“语言”准确的描述出来,计算机才能够解决问题。任意给定一个正实数,设计一个算法求以这个数为半径的圆的面积。
任意给定一个大于1的正整数n,设计一个算法求出n的所有的因数。练习
1.2流程图(程序框图)表1-2
程序框图
结束n不是质数d=d+1返回顺序结构条件结构循环结构程序框图中的三种逻辑结构例3 已知一个三角形的三边边长分别为2,3,4,利用海伦-秦九韶公设计一个算法,求出它的面积,画出算法的程序框图。程序框图开始输出S结束返回例4 任意给定3个正实数,设计一个算法,判断分别
以这3个数为三边边长的三角形是否存在。画出这个
算法的的程序框图。程序框图开始结束输入a,b,ca+b>c,a+c>b,
b+c>a是否同时成立是存在这样的
三角形不存在这样的
三角形否返回例5 设计一个计算1+2+3+…+100的值的算法,并画出程序框图 程序框图开始i=1i<=100?否输出sum结束sum=0i=i+1sum=sum+i是返回
x-2y=-1 (1 )
2x+y=1 (2 )
的求解过程,我们可以归纳出以下步骤:
第一步: (2 )-(1 )×2,得 5y=3;
第二步: 解 ( 3 ) 得y=3/5;
第三步: 将y=3/5代入 ( 1) ,得x=1/5.算法这个词出现于12世纪,指的是用阿拉伯数字进行算术运算的过程。在数学中,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成。按照这样的理解,我们可以设计出很多数学问题的算法。下面看几个例子。例 1 任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定。
算法分析:根据质数的定义,很容易设计出下面的步骤:第一步:判断n是否等于2,若n=2,则n是质数;若n>2,则执行第二步。
第二步:依次从2~(n-1)检验是不是n的因数,即整除n的数。若有这样的数,则n不是质数;若没有这样的数,则n是质数。点评:这是判断一个大于1的整数n是否为质数的最基本的方法例1的程序框图例2 用二分法设计一个求方程x2-2=0的近似根的算法。算法分析:回顾二分法解方程的过程,并假设所求近似根与精确解的差的绝对值不超过0.005,则不难设计出以下步骤:第一步:令 f(x)= x2-2.因为f(1)<0,f(2)>0,所以设x1=1,x2=2.
第二步:令 ,判断f(m)是否为0,若是,则m为所求;若否,则继续判断f(x1) · f(m)大于0还是小于0。
第三步:若f(x1) · f(m)>0,则令x1= m;否则,令x2= m。
第四步:判断 <0.005是否成立?若是,则x1、 x2之间的任意取值均为满足条件的 近似根;若否,则返回第二步。
按照以上步骤,我们将依次得到表1-1和.图1.1-1表1-1
图1.1-1实际上,上述步骤就是在求 的近似值。计算机解决任何问题都要依赖于算法,只有将解决问题的过程分解为若干个明确的步骤,即算法,并用计算机能够接受的“语言”准确的描述出来,计算机才能够解决问题。任意给定一个正实数,设计一个算法求以这个数为半径的圆的面积。
任意给定一个大于1的正整数n,设计一个算法求出n的所有的因数。练习
1.2流程图(程序框图)表1-2
程序框图
结束n不是质数d=d+1返回顺序结构条件结构循环结构程序框图中的三种逻辑结构例3 已知一个三角形的三边边长分别为2,3,4,利用海伦-秦九韶公设计一个算法,求出它的面积,画出算法的程序框图。程序框图开始输出S结束返回例4 任意给定3个正实数,设计一个算法,判断分别
以这3个数为三边边长的三角形是否存在。画出这个
算法的的程序框图。程序框图开始结束输入a,b,ca+b>c,a+c>b,
b+c>a是否同时成立是存在这样的
三角形不存在这样的
三角形否返回例5 设计一个计算1+2+3+…+100的值的算法,并画出程序框图 程序框图开始i=1i<=100?否输出sum结束sum=0i=i+1sum=sum+i是返回
