(北师大版必修3)数学:算法的基本结构及设计(教案)
文档属性
| 名称 | (北师大版必修3)数学:算法的基本结构及设计(教案) |
|
|
| 格式 | rar | ||
| 文件大小 | 232.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-15 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
高一数学算法的基本结构及设计北师大版
【本讲教育信息】
一. 教学内容:
算法的基本结构及设计
二. 学习目标
1、通过模仿、操作、探索,经历通过设计流程图表达解决问题的过程。在具体问题(如三元一次方程组求解等问题)的解决过程中,理解流程图的三种基本逻辑结构:顺序结构、选择结构和循环结构;
2、经过分析具体问题,抽象出算法的过程,培养抽象概括能力、语言表达能力和逻辑思维能力;
3、通过算法实例,体会构造性的思想和方法。
三、知识要点
1、流程图——为了使算法的结构更加清晰,可借助图来帮助描述算法。描述算法的图称为算法流程图或算法框图,简称流程图或框图。21世纪教育网
一般地,我们把“开始”、“结束”框(起止框)画成圆角矩形:
把“输入”、“输出”框画成平行四边形:
把“计算”框(数据处理框)画成矩形:
把“判断”框画成菱形:
2、顺序结构——按照步骤依次执行的一个算法称为具有“顺序结构”的算法,或者称为算法的顺序结构。
3、选择结构——在执行下一个步骤之前需要先进行判断,判断的结果决定后面的步骤,这样的结构称为选择结构。
4、变量——在研究问题的过程中,可以取不同数值的量称为变量。
5、赋值——将某一数值赋给变量的过程称为赋值。在计算机程序设计中,赋值是通过赋值语句实现的,所赋的值可以是数字,也可以是字符串或表达式。不同的程序设计语言中,赋值语句的写法是不一样的,如将数值1赋给变量x,在VB中是用“x=1”实现的,而在C语言中是用“int x=1”实现的。再如,“x=x+1”这个赋值语句执行后,会将此前计算的x的值再加1后的和赋给x(即使得x的值增加了1)。
6、循环结构——在一个算法中,有时有一些步骤需要重复执行,我们把这样的算法结构称为循环结构。其中反复执行的部分称为循环体,控制循环开始和结束的变量称为循环变量。
一个循环结构中必须包括循环体、循环开始的条件和终止的条件(由循环变量控制)。
一般地,循环结构可分为如下两种:
(一)当型(while型)。当型循环在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,不满足则停止;当型循环有时也称为“前测试型”循环(如图1)。
(二)直到型(until型)。直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止。直到型循环又称为“后测试型”循环(如图2)。
对同一个问题,一般来说既可以用当型,又可以用直到型。当然其流程图(即程序框图)是有所不同的。
四、考点解析与典型例题
考点一 有序列直接插入排序算法和折半插入排序算法
对一个给定的有序列(按顺序排列的数据列),插入一个新的数据A,使得新的数据列仍为有序列。有两种算法:直接插入和折半插入。
例1、设计一个算法,在5,7,15,16,25,26中插入20,使得该数据列仍为有序列。
法一:直接插入排序法。
【算理分析】将20与原数据列中的每个数据按从左到右(或从右到左的顺序)逐个比较,以确认该数的位置。
【解】1、20<26,故20在26的左边;
2、20<25,故20在25的左边;
3、20>16,故20在16的右边。
从而,20在16与25之间,新的数据列为:5,7,15,16,20,25,26。
法二:折半插入排序法。
【算理分析】将该数与数据列的中间一个数进行比较,以确认该数在数据列的左或右半部分;再取数据列的左(或右)部分的中间一个数据与该数进行比较,如此循环。
【解】1、因为15<20,故20在数据列的右半部分;
2、因为25>20,故20在右半部分靠左的部分;
3、故20在16和25之间。
【说明】本知识点是对上一讲的一个补充。
考点二 顺序结构的算法流程图
例2、已知梯形两底a、b和高h,设计一个求梯形面积的算法,并画出流程图。
【解】其算法设计如下:
流程图:
21世纪教育网
1. 输入a,b,h;
2. 计算S=(a+b)h;
3.输出S.
考点三 选择结构的算法流程图
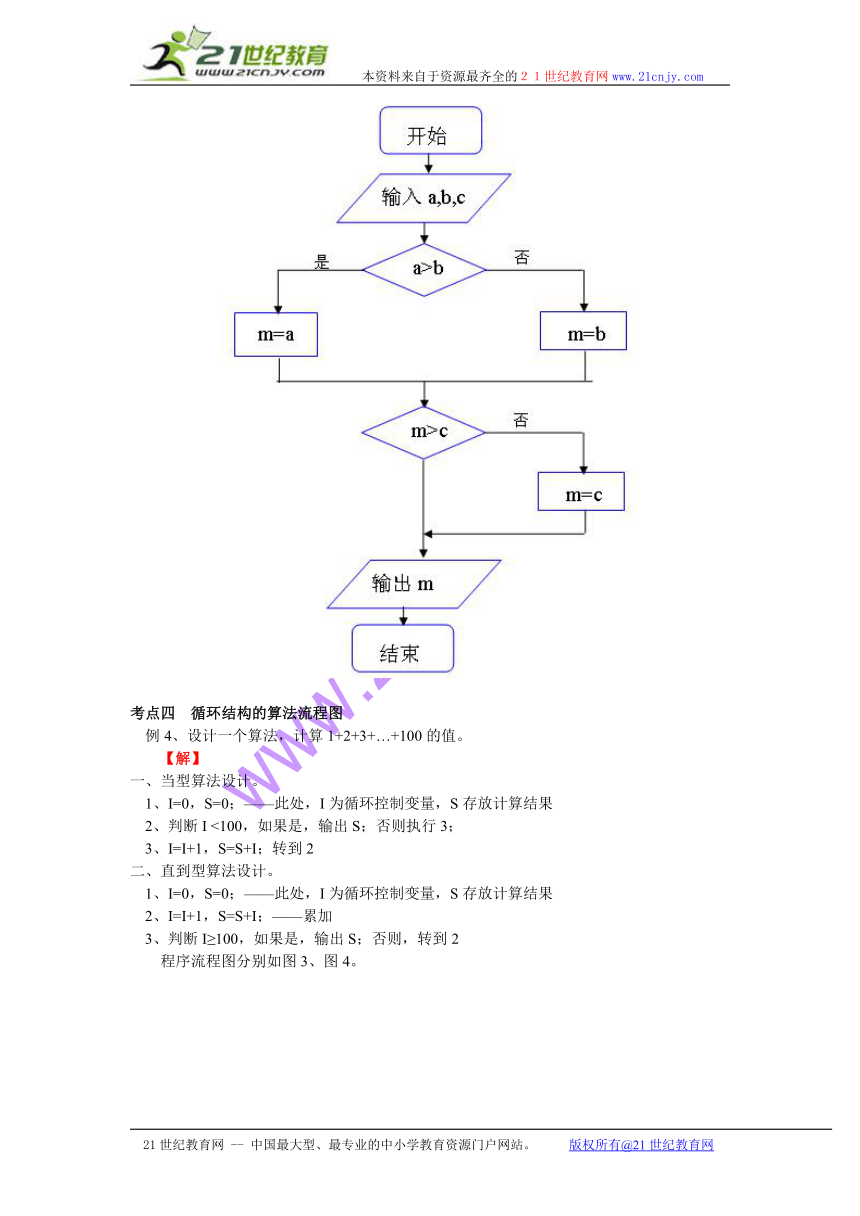
例3、设计一个算法,输出a,b,c中的最大值。
【解】算法设计如下:
1、比较a,b。如果a>b,则执行步骤2,否则执行步骤3;
2、m=a;
3、m=b;
4、比较m,c。如果m>c,则执行步骤5;否则执行步骤6;
5、输出m;
6、m=c;
流程图:
考点四 循环结构的算法流程图
例4、设计一个算法,计算1+2+3+…+100的值。
【解】
一、当型算法设计。
1、I=0,S=0;——此处,I为循环控制变量,S存放计算结果
2、判断I <100,如果是,输出S;否则执行3;
3、I=I+1,S=S+I;转到2
二、直到型算法设计。
1、I=0,S=0;——此处,I为循环控制变量,S存放计算结果
2、I=I+1,S=S+I;——累加
3、判断I≥100,如果是,输出S;否则,转到2
程序流程图分别如图3、图4。
考点五 正确读图,理解算法
例5、下面的程序流程图能判断任意输入的数的奇偶性:
其中判断框内的条件是
A. B. C. D.
【解】“x是偶数”的条件是x除以2的余数是0,本算法以m表示这个余数,故判断框内应填的条件是“m=0”。
【说明】高考对此类题型的考查十分常见。
五、数学思想方法
算法思想是贯穿高中课程的一条主线。算法思想就是程序化地处理问题的思想,指令明确,步骤清晰;但尽管如此,用自然语言描述的算法,尤其是比较复杂的问题的算法,在阅读上仍然有一定的难度,但借助程序流程图(框图)来描述算法则直观易懂;因此,在进行程序设计前我们一般要准确的绘出程序框图。
本讲的学习对于我们正确绘制程序框图、培养算法思想以及逻辑思维能力都有着重要的价值。
【模拟试题】(答题时间:60分钟)
一、选择题
1. 下面的程序框图(如图1),如果输入三个实数a、b、c,要求输出这三个数中最大的数,那么在空白的判断框中,应填入下面四个选项中的
A. c > x B. x > c C. c > b D. b > c
2. 已知直角三角形两直角边长为,,求斜边长的一个算法分下列三步:
①计算;②输入直角三角形两直角边长,的值; ③输出斜边长的值,其中正确的顺序是
A. ①②③ B. ②③① C. ①③② D. ②①③
3. 下图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是
A. i>100 B. i<=100 C. i>50 D. i<=50
4. 给出以下一个算法的程序框图(如图所示),该程序框图的功能是
A. 求输出三数的最大数 B. 求输出三数的最小数
C. 将按从小到大排列 D. 将按从大到小排列
c
5. 阅读如下图所示程序框图,若输入n=5,会输出
A. 3 B. 4 C. 5 D. 6
6. 如图,若输入a=1,b=2,则输出结果为
A、1 B、2 C、3 D、程序有错,无结果
7. 直到型循环结构指的是程序开始后直接执行循环体,“直到条件为真时为止”。 下列循环结构中属于直到型循环结构的为
二、填空题
8. 阅读程序框图,若输入,,则输出 , (注:框图中的赋值符号“”也可以写成“”或“”)
9. 如图执行程序框,若p=0. 8,则输出的n= .
三、解答题
10. 铁路托运行李,从甲地到乙地,按规定每张客票托运行李不超过50㎏时,每千克0. 2元,超过50㎏时,超过部分按每千克0. 25元计算,画出计算行李价格的算法框图.
11. 试设计一个求的算法,并画出流程图。
*12. 设计求1+3+5+7+…+31的流程图
*13. 用二分法设计一个求方程x2-2=0的正近似根的算法(精确到ε=0. 005)。
【试题答案】
1、 选择题
题号 1 2 3 4 5 6 7
答案[来源:21世纪教育网] A D B B A C D
二、填空题
8. 12,3;
9. n=4
三、解答题
10.
11. 输入x;如果x≥0,那么y=1;否则( x<0),得y=-1输出函数值y。
12. 见下图
13. 第一步:令f(x)= x2-2,因为f(1)<0,f(2)>0,则根在区间(1,2)内,设x1=1,x2=2,即根在区间(x1,x2)内。
第二步:令m=,计算f(m)的值,并判断f(m)是否为0。若是,则m为所求根;若否,则继续执行以下步骤。21世纪教育网
第三步:若f(x1) f(m)>0,知f(m) f(x2)<0,则根在区间(m, x2)内,令x1=m;否则根在区间(x1 ,m)内,令x2=m。
第四步:判断|x1-x2|<ε(即|x1-x2|<0. 005)是否成立?若是,则令m=,m为满足条件的近似根;若否,则返回第二步。[来源:21世纪教育网]
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
高一数学算法的基本结构及设计北师大版
【本讲教育信息】
一. 教学内容:
算法的基本结构及设计
二. 学习目标
1、通过模仿、操作、探索,经历通过设计流程图表达解决问题的过程。在具体问题(如三元一次方程组求解等问题)的解决过程中,理解流程图的三种基本逻辑结构:顺序结构、选择结构和循环结构;
2、经过分析具体问题,抽象出算法的过程,培养抽象概括能力、语言表达能力和逻辑思维能力;
3、通过算法实例,体会构造性的思想和方法。
三、知识要点
1、流程图——为了使算法的结构更加清晰,可借助图来帮助描述算法。描述算法的图称为算法流程图或算法框图,简称流程图或框图。21世纪教育网
一般地,我们把“开始”、“结束”框(起止框)画成圆角矩形:
把“输入”、“输出”框画成平行四边形:
把“计算”框(数据处理框)画成矩形:
把“判断”框画成菱形:
2、顺序结构——按照步骤依次执行的一个算法称为具有“顺序结构”的算法,或者称为算法的顺序结构。
3、选择结构——在执行下一个步骤之前需要先进行判断,判断的结果决定后面的步骤,这样的结构称为选择结构。
4、变量——在研究问题的过程中,可以取不同数值的量称为变量。
5、赋值——将某一数值赋给变量的过程称为赋值。在计算机程序设计中,赋值是通过赋值语句实现的,所赋的值可以是数字,也可以是字符串或表达式。不同的程序设计语言中,赋值语句的写法是不一样的,如将数值1赋给变量x,在VB中是用“x=1”实现的,而在C语言中是用“int x=1”实现的。再如,“x=x+1”这个赋值语句执行后,会将此前计算的x的值再加1后的和赋给x(即使得x的值增加了1)。
6、循环结构——在一个算法中,有时有一些步骤需要重复执行,我们把这样的算法结构称为循环结构。其中反复执行的部分称为循环体,控制循环开始和结束的变量称为循环变量。
一个循环结构中必须包括循环体、循环开始的条件和终止的条件(由循环变量控制)。
一般地,循环结构可分为如下两种:
(一)当型(while型)。当型循环在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,不满足则停止;当型循环有时也称为“前测试型”循环(如图1)。
(二)直到型(until型)。直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止。直到型循环又称为“后测试型”循环(如图2)。
对同一个问题,一般来说既可以用当型,又可以用直到型。当然其流程图(即程序框图)是有所不同的。
四、考点解析与典型例题
考点一 有序列直接插入排序算法和折半插入排序算法
对一个给定的有序列(按顺序排列的数据列),插入一个新的数据A,使得新的数据列仍为有序列。有两种算法:直接插入和折半插入。
例1、设计一个算法,在5,7,15,16,25,26中插入20,使得该数据列仍为有序列。
法一:直接插入排序法。
【算理分析】将20与原数据列中的每个数据按从左到右(或从右到左的顺序)逐个比较,以确认该数的位置。
【解】1、20<26,故20在26的左边;
2、20<25,故20在25的左边;
3、20>16,故20在16的右边。
从而,20在16与25之间,新的数据列为:5,7,15,16,20,25,26。
法二:折半插入排序法。
【算理分析】将该数与数据列的中间一个数进行比较,以确认该数在数据列的左或右半部分;再取数据列的左(或右)部分的中间一个数据与该数进行比较,如此循环。
【解】1、因为15<20,故20在数据列的右半部分;
2、因为25>20,故20在右半部分靠左的部分;
3、故20在16和25之间。
【说明】本知识点是对上一讲的一个补充。
考点二 顺序结构的算法流程图
例2、已知梯形两底a、b和高h,设计一个求梯形面积的算法,并画出流程图。
【解】其算法设计如下:
流程图:
21世纪教育网
1. 输入a,b,h;
2. 计算S=(a+b)h;
3.输出S.
考点三 选择结构的算法流程图
例3、设计一个算法,输出a,b,c中的最大值。
【解】算法设计如下:
1、比较a,b。如果a>b,则执行步骤2,否则执行步骤3;
2、m=a;
3、m=b;
4、比较m,c。如果m>c,则执行步骤5;否则执行步骤6;
5、输出m;
6、m=c;
流程图:
考点四 循环结构的算法流程图
例4、设计一个算法,计算1+2+3+…+100的值。
【解】
一、当型算法设计。
1、I=0,S=0;——此处,I为循环控制变量,S存放计算结果
2、判断I <100,如果是,输出S;否则执行3;
3、I=I+1,S=S+I;转到2
二、直到型算法设计。
1、I=0,S=0;——此处,I为循环控制变量,S存放计算结果
2、I=I+1,S=S+I;——累加
3、判断I≥100,如果是,输出S;否则,转到2
程序流程图分别如图3、图4。
考点五 正确读图,理解算法
例5、下面的程序流程图能判断任意输入的数的奇偶性:
其中判断框内的条件是
A. B. C. D.
【解】“x是偶数”的条件是x除以2的余数是0,本算法以m表示这个余数,故判断框内应填的条件是“m=0”。
【说明】高考对此类题型的考查十分常见。
五、数学思想方法
算法思想是贯穿高中课程的一条主线。算法思想就是程序化地处理问题的思想,指令明确,步骤清晰;但尽管如此,用自然语言描述的算法,尤其是比较复杂的问题的算法,在阅读上仍然有一定的难度,但借助程序流程图(框图)来描述算法则直观易懂;因此,在进行程序设计前我们一般要准确的绘出程序框图。
本讲的学习对于我们正确绘制程序框图、培养算法思想以及逻辑思维能力都有着重要的价值。
【模拟试题】(答题时间:60分钟)
一、选择题
1. 下面的程序框图(如图1),如果输入三个实数a、b、c,要求输出这三个数中最大的数,那么在空白的判断框中,应填入下面四个选项中的
A. c > x B. x > c C. c > b D. b > c
2. 已知直角三角形两直角边长为,,求斜边长的一个算法分下列三步:
①计算;②输入直角三角形两直角边长,的值; ③输出斜边长的值,其中正确的顺序是
A. ①②③ B. ②③① C. ①③② D. ②①③
3. 下图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是
A. i>100 B. i<=100 C. i>50 D. i<=50
4. 给出以下一个算法的程序框图(如图所示),该程序框图的功能是
A. 求输出三数的最大数 B. 求输出三数的最小数
C. 将按从小到大排列 D. 将按从大到小排列
c
5. 阅读如下图所示程序框图,若输入n=5,会输出
A. 3 B. 4 C. 5 D. 6
6. 如图,若输入a=1,b=2,则输出结果为
A、1 B、2 C、3 D、程序有错,无结果
7. 直到型循环结构指的是程序开始后直接执行循环体,“直到条件为真时为止”。 下列循环结构中属于直到型循环结构的为
二、填空题
8. 阅读程序框图,若输入,,则输出 , (注:框图中的赋值符号“”也可以写成“”或“”)
9. 如图执行程序框,若p=0. 8,则输出的n= .
三、解答题
10. 铁路托运行李,从甲地到乙地,按规定每张客票托运行李不超过50㎏时,每千克0. 2元,超过50㎏时,超过部分按每千克0. 25元计算,画出计算行李价格的算法框图.
11. 试设计一个求的算法,并画出流程图。
*12. 设计求1+3+5+7+…+31的流程图
*13. 用二分法设计一个求方程x2-2=0的正近似根的算法(精确到ε=0. 005)。
【试题答案】
1、 选择题
题号 1 2 3 4 5 6 7
答案[来源:21世纪教育网] A D B B A C D
二、填空题
8. 12,3;
9. n=4
三、解答题
10.
11. 输入x;如果x≥0,那么y=1;否则( x<0),得y=-1输出函数值y。
12. 见下图
13. 第一步:令f(x)= x2-2,因为f(1)<0,f(2)>0,则根在区间(1,2)内,设x1=1,x2=2,即根在区间(x1,x2)内。
第二步:令m=,计算f(m)的值,并判断f(m)是否为0。若是,则m为所求根;若否,则继续执行以下步骤。21世纪教育网
第三步:若f(x1) f(m)>0,知f(m) f(x2)<0,则根在区间(m, x2)内,令x1=m;否则根在区间(x1 ,m)内,令x2=m。
第四步:判断|x1-x2|<ε(即|x1-x2|<0. 005)是否成立?若是,则令m=,m为满足条件的近似根;若否,则返回第二步。[来源:21世纪教育网]
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
