实际问题与一元一次方程
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
实际问题与一元一次方程
教学目标
(1)建立实际问题的方程模型,运用一元一次方程分析和解决实际问题.
(2)根据问题的实际背景进行检验,利用方程进行简单推理判断.
价值.
教学重点、难点:
重点:建立实际问题的方程模型,运用一元一次方程分析和解决实际问题.
难点:正确地建立方程.
一、创设情景
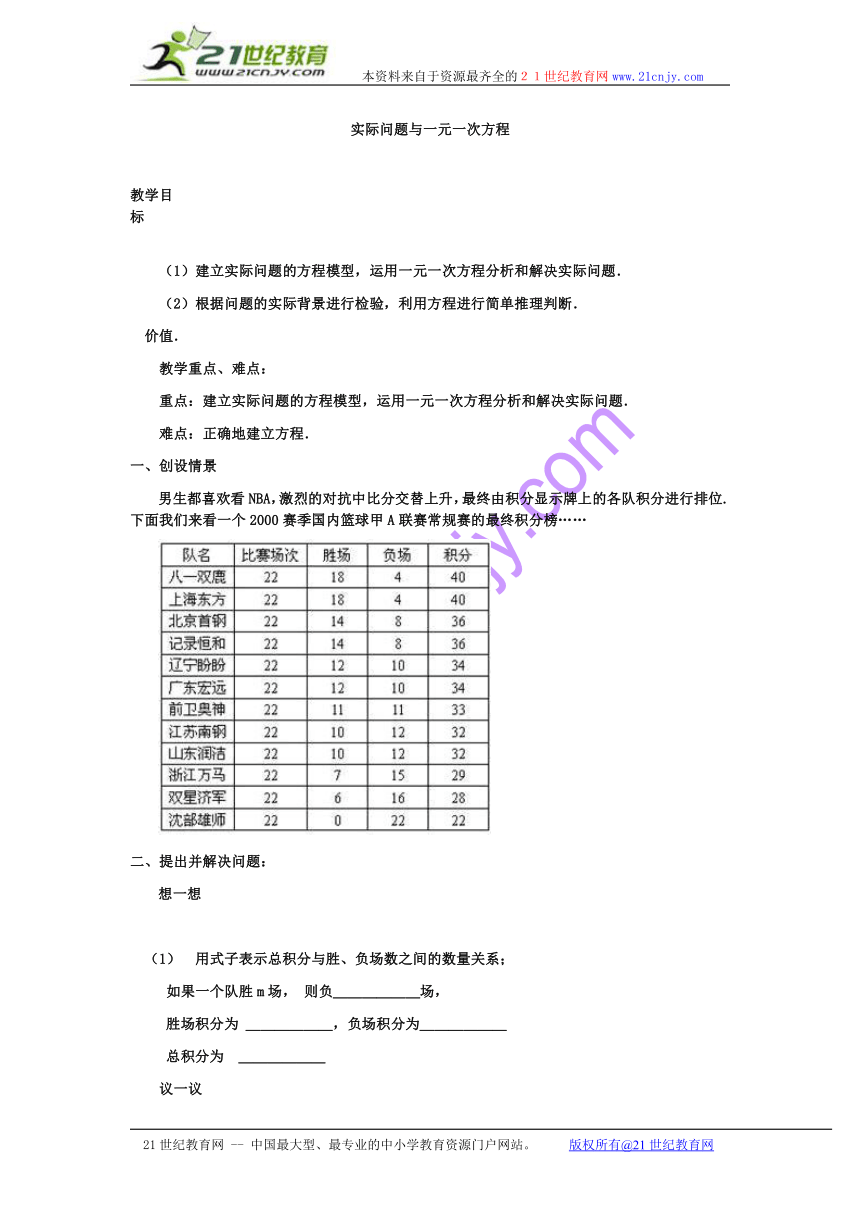
男生都喜欢看NBA,激烈的对抗中比分交替上升,最终由积分显示牌上的各队积分进行排位.下面我们来看一个2000赛季国内篮球甲A联赛常规赛的最终积分榜……
二、提出并解决问题:
想一想
(1) 用式子表示总积分与胜、负场数之间的数量关系;
如果一个队胜m场, 则负______场,
胜场积分为 ______,负场积分为______
总积分为 ______
议一议
(2) 某队的胜场总积分能等于它的负场总积分吗?
设一个队胜了x场,则负了______场,如果这个队的胜场总积分等于负场总积分,则有方程 ______
计算得 ______
问题:x表示什么量?它可以是分数吗?
x表示某队获胜的场数,它应该是自然数,不能是分数22/3.所以x=22/3不符合实际.
问题:由此你得出什么结论?
可以判定没有哪个队的胜场总积分等于负场总积分.
(3) 问题:“观察积分表,你能选择出其中一行说明负一场积几分吗?”
设胜一场积x分的话,从表中其他任何一行可以列方程,求出x的值
从第一行得出方程:
18x+1×4=40
由此得出
x=2
用表中其他行可以验证,得出结论:____________.
小注:(!)
(2)
三 总结质疑:
这节课有哪些收获?你还有哪些问题?
四 练习尝试
《A》大家一起做
一、选择题:
1.陈华以8折的优惠价购得一双鞋子节省了20元,则他买鞋子实际用了( )
A.60元 B.80元 C.100元 D.150元
2.甲仓库存煤200吨,乙仓库存煤70吨,若甲仓库每天运出15吨煤,乙仓库每天运进25吨煤,几天后乙仓库存煤比甲仓库多1倍?设x天后乙仓库存煤比甲仓库多1倍,则有( )
A.2×15x = 25x B.70+25x 15x = 200×2
C.2(200 15x) = 70+25x D.200 15x = 2(70+25x) .
3.某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个,则可以超额5个,问规定时间是多少?设规定的时间为x,则有( )
A.38x 15 = 42x+5 B.38x+15 = 42x 5
C.42x+38x = 15+5 D.42x 28x = 15 5
4.三少年年龄之和为33,多少年后三人的年龄之和为现在年龄之和的两倍?设x年后三人年龄之和为现在年龄的2倍,则有( )
A.3x = 2×33 B.3x 33 = 2× 33
C.3x+33 = 2×33 D.3x = 3×33
〈B〉相信你能行
二、列方程解应用题:
1.要加工200个零件,甲先单独加工了5小时,然后又与乙一起加工了4小时,完成了任务,已知甲每小时比乙每小时多加工2个零件,求甲、乙每小时各加工多少零件?
2.学校开展植树活动,甲班和乙班共植树31株,其中甲班植树数比乙班植树数的2倍多1株,求两班各植树多少株?
3.某商店购买大件商品实行分期付款,小明的爸爸买了一台9000元的电脑,第一次付款30%,以后每月付450元,需要多长时间才能付完?
4.服装厂要生产某种型号的学生服装一批,已知 3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,库内存有这样的布料 600m,应分别用多少布料做上衣,多少布料做裤子才能恰好配套?
5.甲步行上午6时从A地出发于下午5时到达B地,乙骑自行车上午10时从A地出发,于下午是3时到达B地;问乙是在什么时间追上甲的?
6.有一架飞机,最多能在空中连续飞行6h,它在飞出和返回时的速度分别是 900km/h和 850km/h,这架飞机最远飞出多少千米就应返回?(精确到 1km)
7.某校组织初一学生外出进行科技活动,需租用客车若干辆,现有50座的和45座的两种客车,若租用50座的客车刚好坐满,若租用同样数量的45座的客车则有30人无座位.
(1)初一年级有多少学生?
(2)若50座、45座车的日租金分别为每辆300元和250元,且只能租用一种型号的客车,哪种方案合算?
8.某售楼中心对某住宅楼的标价是:基价为2580元/m2,楼层差价如下表:(“+”表示上浮,“ ”表示下浮).
某人买了面积为 90平方米的三楼,若他花同样多的钱去买六楼,则可多买几平方米?
9.航船从A码头顺流而下到达B码头,然后逆流返回到达A、B之间的C码头,一共航行了7小时,已知此船在静水中的速度为 7.5千米/小时,水流速度为 2.5千米/小时,A、C码头间的航程为 10千米,求A、B码头间的航程.如果A码头在B、C码头之间,那么A、B码头间的航程又是多少千米?
一、选择题:
1.陈华以8折的优惠价购得一双鞋子节省了20元,则他买鞋子实际用了( )
A.60元 B.80元 C.100元 D.150元
说明:设他买鞋子实际用了x元,则根据题意鞋子的原价则是(x+20)元,因此有(x+20) 80% = x,化简得0.8x+16 = x,解得x = 80,所以答案为B.
2.甲仓库存煤200吨,乙仓库存煤70吨,若甲仓库每天运出15吨煤,乙仓库每天运进25吨煤,几天后乙仓库存煤比甲仓库多1倍?设x天后乙仓库存煤比甲仓库多1倍,则有( )
A.2×15x = 25x B.70+25x 15x = 200×2
C.2(200 15x) = 70+25x D.200 15x = 2(70+25x)
说明:乙仓库存煤比甲仓库多1倍,即乙仓库存煤是甲仓库的2倍;根据题意x天后乙仓库的存煤为70+25x,甲仓库x天后的存煤为200 15x,则70+25x = 2(200 15x),所以正确答案为C.
3.某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个,则可以超额5个,问规定时间是多少?设规定的时间为x,则有( )
A.38x 15 = 42x+5 B.38x+15 = 42x 5
C.42x+38x = 15+5 D.42x 28x = 15 5
说明:每小时生产38个零件,则规定时间可生产38x个零件,总零件数为38x+15;每小时生产42个,规定时间则可生产42x个,总零件数为42x 5,因此,38x+15 = 42x 5,答案为B.
4.三少年年龄之和为33,多少年后三人的年龄之和为现在年龄之和的两倍?设x年后三人年龄之和为现在年龄的2倍,则有( )
A.3x = 2×33 B.3x 33 = 2× 33 C.3x+33 = 2×33 D.3x = 3×33
说明:三个x年后年龄之和比现在增长3x,因此,现在的年龄之和增长3x后,应该是现在年龄之和的两倍,即33+3x = 2×33,答案为C.
二、列方程解应用题:
1.要加工200个零件,甲先单独加工了5小时,然后又与乙一起加工了4小时,完成了任务,已知甲每小时比乙每小时多加工2个零件,求甲、乙每小时各加工多少零件?
解:设乙每小时加工x个零件,则甲每小时加工(x+2)个零件
由题意得
5(x+2)+4(x+x+2) = 200
∴x = 14,x+2 = 16
答:甲每小时加工16个,乙每小时加工14个零件.
2.学校开展植树活动,甲班和乙班共植树31株,其中甲班植树数比乙班植树数的2倍多1株,求两班各植树多少株?
解:设甲班植树x株,则乙班植树(31 x)株
由题意得x = 2(31 x)+1
∴x = 21,31 x = 10
答:甲班植树21株,乙班植树10株.
3.某商店购买大件商品实行分期付款,小明的爸爸买了一台9000元的电脑,第一次付款30%,以后每月付450元,需要多长时间才能付完?
解:设需x个月可以付完
则450x+9000×30% = 9000,解得x = 14
答:14个月付完.
4.服装厂要生产某种型号的学生服装一批,已知 3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,库内存有这样的布料 600m,应分别用多少布料做上衣,多少布料做裤子才能恰好配套?
解:设做上衣的布料用x m,则做裤子的布料用(600 x)m;由题意知
×2 =×3
∴x = 360,600 x = 240
答:取 360m做上衣,剩下做裤子.
5.甲步行上午6时从A地出发于下午5时到达B地,乙骑自行车上午10时从A地出发,于下午是3时到达B地;问乙是在什么时间追上甲的?
解:甲从上午6时到下午5时,共11小时走完全程,乙用5小时走完全程
设乙出发后x小时与甲相遇,则x =x+
∴x = 3(小时)(3小时20分钟)
答:在下午1:20分乙追上甲.
6.有一架飞机,最多能在空中连续飞行6h,它在飞出和返回时的速度分别是 900km/h和 850km/h,这架飞机最远飞出多少千米就应返回?(精确到 1km)
解:设最远飞出s km就应返回;
则+= 6
∴s = 2622.857
∴取s = 2622
答:飞机飞出的最远距离为2622 km.
7.某校组织初一学生外出进行科技活动,需租用客车若干辆,现有50座的和45座的两种客车,若租用50座的客车刚好坐满,若租用同样数量的45座的客车则有30人无座位.
(1)初一年级有多少学生?
(2)若50座、45座车的日租金分别为每辆300元和250元,且只能租用一种型号的客车,哪种方案合算?
解析:(1)设计划租用50座客车x辆,则初一学生人数为50x,按租用45座客车计算,初一学生人数为45x+30.由题意得
50x = 45x+30
5x = 30
x = 6.
∴初一学生人数为50×6 = 300.
另法:设初一学生人数为x,则需租用50座客车辆,从总人数中减去30,需租用45座客车的辆数是,由题意得
=
9x = 10(x 30)
9x = 10x 300
x = 300.
评注:这两种解法中,应用的等量关系分别是初一学生的人数,租用客车的辆数.
(2)∵租用50座客车的总租金是300×6 = 1800(元)
租用45座客车的总租金是250×(6+1) = 1750(元)
∴租用45座客车7辆合算.
8.某售楼中心对某住宅楼的标价是:基价为2580元/m2,楼层差价如下表:(“+”表示上浮,“ ”表示下浮).
某人买了面积为 90平方米的三楼,若他花同样多的钱去买六楼,则可多买几平方米?
解析:设买六楼可多买x平方米,则买(90+x)平方米的六楼的房花钱2580×(1 10%)×(90+x)元,这钱数和买 90平方米三楼房花钱2580×(1+18%)×90元相等.
于是得
2580×(1 10%)×(90+x) = 2580×(1+18%)×90
0.9×(90+x) = 1.18×90
81+0.9x = 106.2
0.9x = 25.2
x = 28.
答:买六楼房子可多买 28平方米.
9.航船从A码头顺流而下到达B码头,然后逆流返回到达A、B之间的C码头,一共航行了7小时,已知此船在静水中的速度为 7.5千米/小时,水流速度为 2.5千米/小时,A、C码头间的航程为 10千米,求A、B码头间的航程.如果A码头在B、C码头之间,那么A、B码头间的航程又是多少千米?
解析:当C在A、B间时,如图
设B、C间的航程为x千米,则航船从A到B顺流而下的时间时小时,然后从B到C逆流而上的时间是小时,由题意得
+= 7
+=7
(10+x)+2x = 70
3x = 60
x = 20
x+10 = 30
解析:当A在B、C间时,如图
设A、B间的航程为x千米,则航船从A到B顺流而下的时间是小时,然后从B到C逆流而上的时间是小时,由题意得
+= 7
+= 7
x+2(10+x) = 70
x+20+2x = 70
3x = 50
x = 16.
答:当C在A、B间时,A、B间的航程是 30千米;当A在B、C间时,A、B间的航程是 16 千米.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
实际问题与一元一次方程
教学目标
(1)建立实际问题的方程模型,运用一元一次方程分析和解决实际问题.
(2)根据问题的实际背景进行检验,利用方程进行简单推理判断.
价值.
教学重点、难点:
重点:建立实际问题的方程模型,运用一元一次方程分析和解决实际问题.
难点:正确地建立方程.
一、创设情景
男生都喜欢看NBA,激烈的对抗中比分交替上升,最终由积分显示牌上的各队积分进行排位.下面我们来看一个2000赛季国内篮球甲A联赛常规赛的最终积分榜……
二、提出并解决问题:
想一想
(1) 用式子表示总积分与胜、负场数之间的数量关系;
如果一个队胜m场, 则负______场,
胜场积分为 ______,负场积分为______
总积分为 ______
议一议
(2) 某队的胜场总积分能等于它的负场总积分吗?
设一个队胜了x场,则负了______场,如果这个队的胜场总积分等于负场总积分,则有方程 ______
计算得 ______
问题:x表示什么量?它可以是分数吗?
x表示某队获胜的场数,它应该是自然数,不能是分数22/3.所以x=22/3不符合实际.
问题:由此你得出什么结论?
可以判定没有哪个队的胜场总积分等于负场总积分.
(3) 问题:“观察积分表,你能选择出其中一行说明负一场积几分吗?”
设胜一场积x分的话,从表中其他任何一行可以列方程,求出x的值
从第一行得出方程:
18x+1×4=40
由此得出
x=2
用表中其他行可以验证,得出结论:____________.
小注:(!)
(2)
三 总结质疑:
这节课有哪些收获?你还有哪些问题?
四 练习尝试
《A》大家一起做
一、选择题:
1.陈华以8折的优惠价购得一双鞋子节省了20元,则他买鞋子实际用了( )
A.60元 B.80元 C.100元 D.150元
2.甲仓库存煤200吨,乙仓库存煤70吨,若甲仓库每天运出15吨煤,乙仓库每天运进25吨煤,几天后乙仓库存煤比甲仓库多1倍?设x天后乙仓库存煤比甲仓库多1倍,则有( )
A.2×15x = 25x B.70+25x 15x = 200×2
C.2(200 15x) = 70+25x D.200 15x = 2(70+25x) .
3.某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个,则可以超额5个,问规定时间是多少?设规定的时间为x,则有( )
A.38x 15 = 42x+5 B.38x+15 = 42x 5
C.42x+38x = 15+5 D.42x 28x = 15 5
4.三少年年龄之和为33,多少年后三人的年龄之和为现在年龄之和的两倍?设x年后三人年龄之和为现在年龄的2倍,则有( )
A.3x = 2×33 B.3x 33 = 2× 33
C.3x+33 = 2×33 D.3x = 3×33
〈B〉相信你能行
二、列方程解应用题:
1.要加工200个零件,甲先单独加工了5小时,然后又与乙一起加工了4小时,完成了任务,已知甲每小时比乙每小时多加工2个零件,求甲、乙每小时各加工多少零件?
2.学校开展植树活动,甲班和乙班共植树31株,其中甲班植树数比乙班植树数的2倍多1株,求两班各植树多少株?
3.某商店购买大件商品实行分期付款,小明的爸爸买了一台9000元的电脑,第一次付款30%,以后每月付450元,需要多长时间才能付完?
4.服装厂要生产某种型号的学生服装一批,已知 3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,库内存有这样的布料 600m,应分别用多少布料做上衣,多少布料做裤子才能恰好配套?
5.甲步行上午6时从A地出发于下午5时到达B地,乙骑自行车上午10时从A地出发,于下午是3时到达B地;问乙是在什么时间追上甲的?
6.有一架飞机,最多能在空中连续飞行6h,它在飞出和返回时的速度分别是 900km/h和 850km/h,这架飞机最远飞出多少千米就应返回?(精确到 1km)
7.某校组织初一学生外出进行科技活动,需租用客车若干辆,现有50座的和45座的两种客车,若租用50座的客车刚好坐满,若租用同样数量的45座的客车则有30人无座位.
(1)初一年级有多少学生?
(2)若50座、45座车的日租金分别为每辆300元和250元,且只能租用一种型号的客车,哪种方案合算?
8.某售楼中心对某住宅楼的标价是:基价为2580元/m2,楼层差价如下表:(“+”表示上浮,“ ”表示下浮).
某人买了面积为 90平方米的三楼,若他花同样多的钱去买六楼,则可多买几平方米?
9.航船从A码头顺流而下到达B码头,然后逆流返回到达A、B之间的C码头,一共航行了7小时,已知此船在静水中的速度为 7.5千米/小时,水流速度为 2.5千米/小时,A、C码头间的航程为 10千米,求A、B码头间的航程.如果A码头在B、C码头之间,那么A、B码头间的航程又是多少千米?
一、选择题:
1.陈华以8折的优惠价购得一双鞋子节省了20元,则他买鞋子实际用了( )
A.60元 B.80元 C.100元 D.150元
说明:设他买鞋子实际用了x元,则根据题意鞋子的原价则是(x+20)元,因此有(x+20) 80% = x,化简得0.8x+16 = x,解得x = 80,所以答案为B.
2.甲仓库存煤200吨,乙仓库存煤70吨,若甲仓库每天运出15吨煤,乙仓库每天运进25吨煤,几天后乙仓库存煤比甲仓库多1倍?设x天后乙仓库存煤比甲仓库多1倍,则有( )
A.2×15x = 25x B.70+25x 15x = 200×2
C.2(200 15x) = 70+25x D.200 15x = 2(70+25x)
说明:乙仓库存煤比甲仓库多1倍,即乙仓库存煤是甲仓库的2倍;根据题意x天后乙仓库的存煤为70+25x,甲仓库x天后的存煤为200 15x,则70+25x = 2(200 15x),所以正确答案为C.
3.某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个,则可以超额5个,问规定时间是多少?设规定的时间为x,则有( )
A.38x 15 = 42x+5 B.38x+15 = 42x 5
C.42x+38x = 15+5 D.42x 28x = 15 5
说明:每小时生产38个零件,则规定时间可生产38x个零件,总零件数为38x+15;每小时生产42个,规定时间则可生产42x个,总零件数为42x 5,因此,38x+15 = 42x 5,答案为B.
4.三少年年龄之和为33,多少年后三人的年龄之和为现在年龄之和的两倍?设x年后三人年龄之和为现在年龄的2倍,则有( )
A.3x = 2×33 B.3x 33 = 2× 33 C.3x+33 = 2×33 D.3x = 3×33
说明:三个x年后年龄之和比现在增长3x,因此,现在的年龄之和增长3x后,应该是现在年龄之和的两倍,即33+3x = 2×33,答案为C.
二、列方程解应用题:
1.要加工200个零件,甲先单独加工了5小时,然后又与乙一起加工了4小时,完成了任务,已知甲每小时比乙每小时多加工2个零件,求甲、乙每小时各加工多少零件?
解:设乙每小时加工x个零件,则甲每小时加工(x+2)个零件
由题意得
5(x+2)+4(x+x+2) = 200
∴x = 14,x+2 = 16
答:甲每小时加工16个,乙每小时加工14个零件.
2.学校开展植树活动,甲班和乙班共植树31株,其中甲班植树数比乙班植树数的2倍多1株,求两班各植树多少株?
解:设甲班植树x株,则乙班植树(31 x)株
由题意得x = 2(31 x)+1
∴x = 21,31 x = 10
答:甲班植树21株,乙班植树10株.
3.某商店购买大件商品实行分期付款,小明的爸爸买了一台9000元的电脑,第一次付款30%,以后每月付450元,需要多长时间才能付完?
解:设需x个月可以付完
则450x+9000×30% = 9000,解得x = 14
答:14个月付完.
4.服装厂要生产某种型号的学生服装一批,已知 3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,库内存有这样的布料 600m,应分别用多少布料做上衣,多少布料做裤子才能恰好配套?
解:设做上衣的布料用x m,则做裤子的布料用(600 x)m;由题意知
×2 =×3
∴x = 360,600 x = 240
答:取 360m做上衣,剩下做裤子.
5.甲步行上午6时从A地出发于下午5时到达B地,乙骑自行车上午10时从A地出发,于下午是3时到达B地;问乙是在什么时间追上甲的?
解:甲从上午6时到下午5时,共11小时走完全程,乙用5小时走完全程
设乙出发后x小时与甲相遇,则x =x+
∴x = 3(小时)(3小时20分钟)
答:在下午1:20分乙追上甲.
6.有一架飞机,最多能在空中连续飞行6h,它在飞出和返回时的速度分别是 900km/h和 850km/h,这架飞机最远飞出多少千米就应返回?(精确到 1km)
解:设最远飞出s km就应返回;
则+= 6
∴s = 2622.857
∴取s = 2622
答:飞机飞出的最远距离为2622 km.
7.某校组织初一学生外出进行科技活动,需租用客车若干辆,现有50座的和45座的两种客车,若租用50座的客车刚好坐满,若租用同样数量的45座的客车则有30人无座位.
(1)初一年级有多少学生?
(2)若50座、45座车的日租金分别为每辆300元和250元,且只能租用一种型号的客车,哪种方案合算?
解析:(1)设计划租用50座客车x辆,则初一学生人数为50x,按租用45座客车计算,初一学生人数为45x+30.由题意得
50x = 45x+30
5x = 30
x = 6.
∴初一学生人数为50×6 = 300.
另法:设初一学生人数为x,则需租用50座客车辆,从总人数中减去30,需租用45座客车的辆数是,由题意得
=
9x = 10(x 30)
9x = 10x 300
x = 300.
评注:这两种解法中,应用的等量关系分别是初一学生的人数,租用客车的辆数.
(2)∵租用50座客车的总租金是300×6 = 1800(元)
租用45座客车的总租金是250×(6+1) = 1750(元)
∴租用45座客车7辆合算.
8.某售楼中心对某住宅楼的标价是:基价为2580元/m2,楼层差价如下表:(“+”表示上浮,“ ”表示下浮).
某人买了面积为 90平方米的三楼,若他花同样多的钱去买六楼,则可多买几平方米?
解析:设买六楼可多买x平方米,则买(90+x)平方米的六楼的房花钱2580×(1 10%)×(90+x)元,这钱数和买 90平方米三楼房花钱2580×(1+18%)×90元相等.
于是得
2580×(1 10%)×(90+x) = 2580×(1+18%)×90
0.9×(90+x) = 1.18×90
81+0.9x = 106.2
0.9x = 25.2
x = 28.
答:买六楼房子可多买 28平方米.
9.航船从A码头顺流而下到达B码头,然后逆流返回到达A、B之间的C码头,一共航行了7小时,已知此船在静水中的速度为 7.5千米/小时,水流速度为 2.5千米/小时,A、C码头间的航程为 10千米,求A、B码头间的航程.如果A码头在B、C码头之间,那么A、B码头间的航程又是多少千米?
解析:当C在A、B间时,如图
设B、C间的航程为x千米,则航船从A到B顺流而下的时间时小时,然后从B到C逆流而上的时间是小时,由题意得
+= 7
+=7
(10+x)+2x = 70
3x = 60
x = 20
x+10 = 30
解析:当A在B、C间时,如图
设A、B间的航程为x千米,则航船从A到B顺流而下的时间是小时,然后从B到C逆流而上的时间是小时,由题意得
+= 7
+= 7
x+2(10+x) = 70
x+20+2x = 70
3x = 50
x = 16.
答:当C在A、B间时,A、B间的航程是 30千米;当A在B、C间时,A、B间的航程是 16 千米.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
