11.2三角形全等判定(3)
文档属性
| 名称 | 11.2三角形全等判定(3) |  | |
| 格式 | rar | ||
| 文件大小 | 924.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-16 21:29:00 | ||
图片预览




文档简介
课件18张PPT。 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——古希腊数学家:毕达哥拉斯
安陆市接官乡初级中学 董成伟人教版八年级数学 第十一章 11. 2
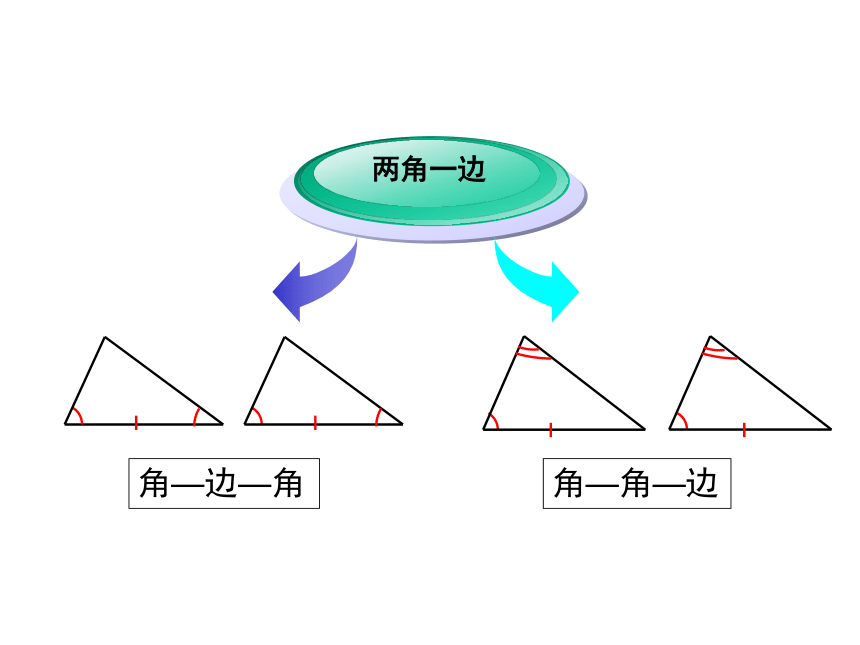
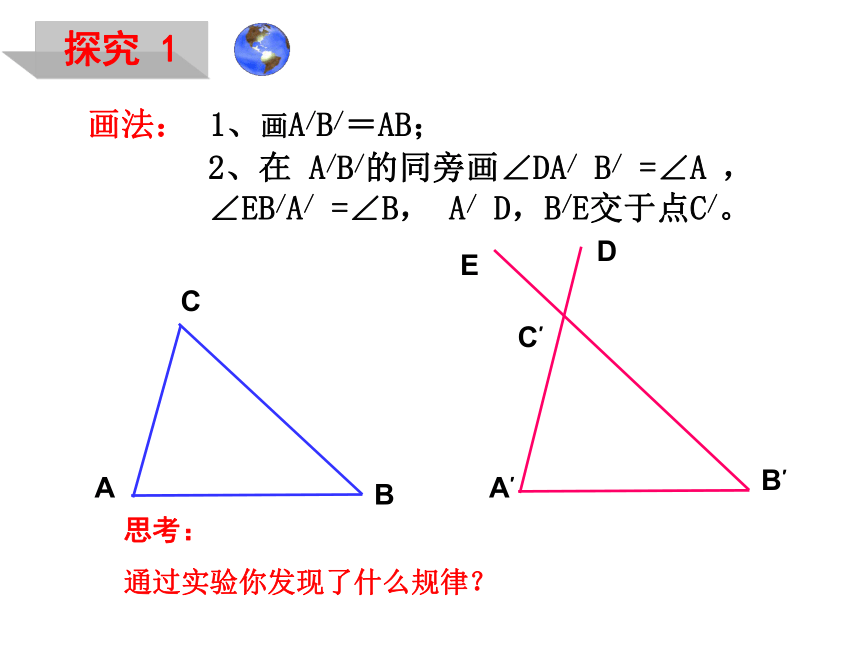
三角形全等的判定(三)①三角;②三边;③两边一角;④两角一边。 回 顾 如果给出三个条件画三角形,你能说出有哪几种可能的情况?角—边—角 角—角—边 先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B (即使两角和它们的夹边对应相等)。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗? 探究 1画法:2、在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/。1、画A/B/=AB;思考:
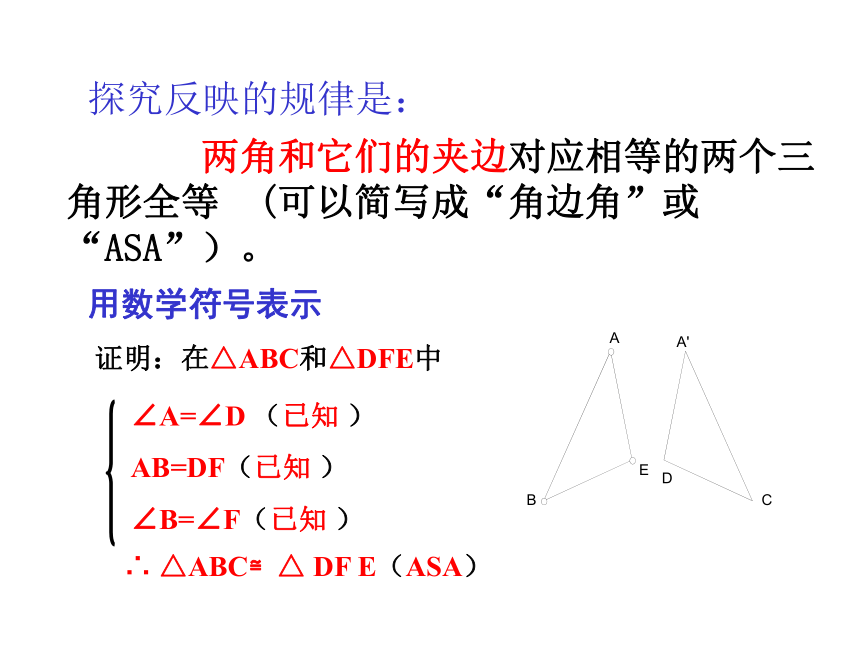
通过实验你发现了什么规律?A′B′C′ED 探究 1 两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角”或“ASA”)。探究反映的规律是:用数学符号表示 如下图,在△ABC和△DEF中,∠A =∠D ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?BACEFD 探究 2 探究2反映的规律是:
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。用数学符号表示ABCDEF 1.如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C。 求证 AD=AE。 应用提高 应用提高 2.已知,如图,∠1=∠2,∠C=∠D。求证:AC=AD。
证明:
在△ABD和△ABC中
∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
证明:
∵AB⊥BC,AD⊥DC
∴∠B=∠D=90°
在△ABC和△ADC中
∠B=∠D=90° (已证)
∠1=∠2(对顶角)
AC=AC(公共边)
∴△ABC≌△ADC (AAS)
∴AB=AD (全等三角形对应边相等)
解:
在△ABC和△EDC中
∠B=∠D=90° (已知)
BC=DC(公共边)
∠ACB=∠ECD(对顶角)
∴△ABD≌△ABC (ASA)
∴DE=AB (全等三角形对应边相等) 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?(2)(1)请你帮帮忙!①三角;②三边;③两边一角;④两角一边。归纳小结 如果给出三个条件画三角形,你能说出有哪几种可能的情况?只给三个条件 到目前为止,我们一共探索出判定三角形全等的方法有哪些?
1、边边边(SSS)3、角边角(ASA)4、角角边(AAS)2、边角边(SAS)归纳小结学习小结 你能谈谈学习这节课内容后的收获和体会吗? 习题11.2
第5、6题。再 见!
——古希腊数学家:毕达哥拉斯
安陆市接官乡初级中学 董成伟人教版八年级数学 第十一章 11. 2
三角形全等的判定(三)①三角;②三边;③两边一角;④两角一边。 回 顾 如果给出三个条件画三角形,你能说出有哪几种可能的情况?角—边—角 角—角—边 先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B (即使两角和它们的夹边对应相等)。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗? 探究 1画法:2、在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/。1、画A/B/=AB;思考:
通过实验你发现了什么规律?A′B′C′ED 探究 1 两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角”或“ASA”)。探究反映的规律是:用数学符号表示 如下图,在△ABC和△DEF中,∠A =∠D ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?BACEFD 探究 2 探究2反映的规律是:
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。用数学符号表示ABCDEF 1.如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C。 求证 AD=AE。 应用提高 应用提高 2.已知,如图,∠1=∠2,∠C=∠D。求证:AC=AD。
证明:
在△ABD和△ABC中
∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
证明:
∵AB⊥BC,AD⊥DC
∴∠B=∠D=90°
在△ABC和△ADC中
∠B=∠D=90° (已证)
∠1=∠2(对顶角)
AC=AC(公共边)
∴△ABC≌△ADC (AAS)
∴AB=AD (全等三角形对应边相等)
解:
在△ABC和△EDC中
∠B=∠D=90° (已知)
BC=DC(公共边)
∠ACB=∠ECD(对顶角)
∴△ABD≌△ABC (ASA)
∴DE=AB (全等三角形对应边相等) 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?(2)(1)请你帮帮忙!①三角;②三边;③两边一角;④两角一边。归纳小结 如果给出三个条件画三角形,你能说出有哪几种可能的情况?只给三个条件 到目前为止,我们一共探索出判定三角形全等的方法有哪些?
1、边边边(SSS)3、角边角(ASA)4、角角边(AAS)2、边角边(SAS)归纳小结学习小结 你能谈谈学习这节课内容后的收获和体会吗? 习题11.2
第5、6题。再 见!
