(新人教a版必修4)数学:3.1.1《两角差的余弦公式》课件
文档属性
| 名称 | (新人教a版必修4)数学:3.1.1《两角差的余弦公式》课件 |
|
|
| 格式 | rar | ||
| 文件大小 | 78.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-15 19:58:00 | ||
图片预览




文档简介
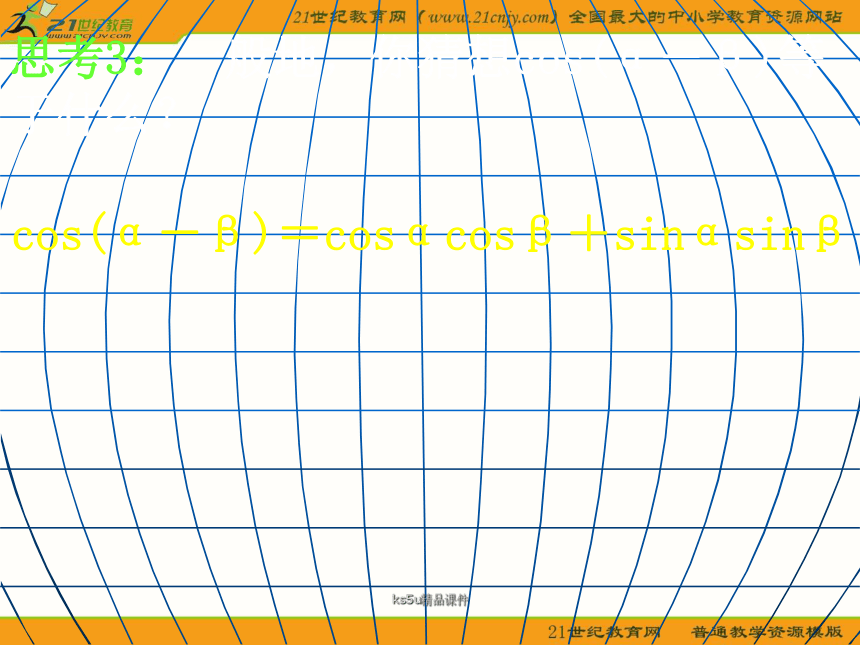
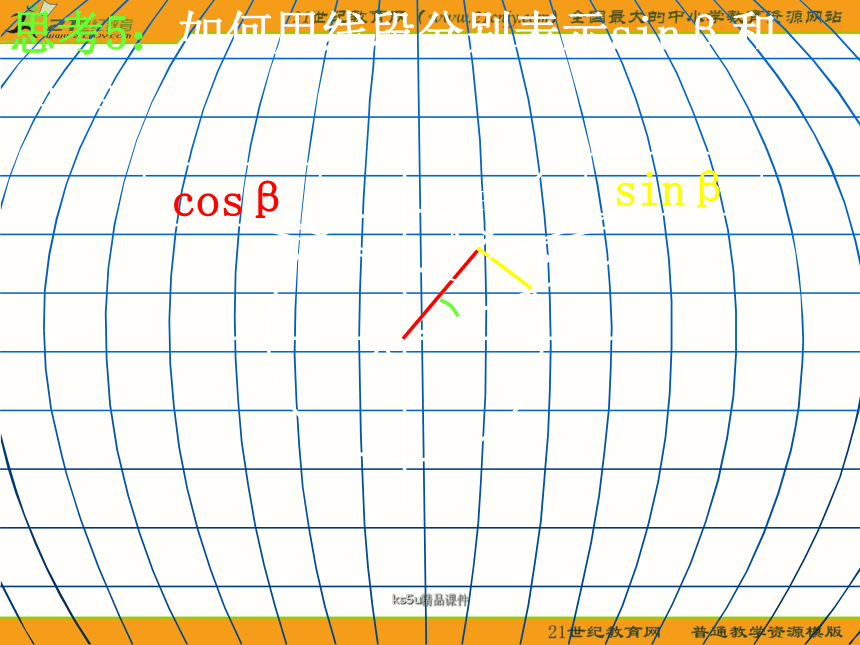
课件21张PPT。ks5u精品课件3.1 两角和与差的正弦、余弦 和正切公式3.1.1 两角差的余弦公式ks5u精品课件问题提出1.在三角函数中,我们学习了哪些基本的三角函数公式? 2.对于30°,45°,60°等特殊角的三角函数值可以直接写出,利用诱导公式还可进一步求出150°,210°,315°等角的三角函数值.我们希望再引进一些公式,能够求更多的非特殊角的三角函数值,同时也为三角恒等变换提供理论依据.ks5u精品课件3.若已知α,β的三角函数值,那么cos(α-β)的值是否确定?它与α,β的三角函数值有什么关系?这是我们需要探索的问题. ks5u精品课件两角差的余弦公式 ks5u精品课件探究(一):两角差的余弦公式 思考1:设α,β为两个任意角, 你能判断cos(α-β)=cosα-cosβ恒成立吗?cos(30°-30°)≠cos30°-cos30°ks5u精品课件思考2:我们设想cos(α-β)的值与α,β的三角函数值有一定关系,观察下表中的数据,你有什么发现?ks5u精品课件思考3:一般地,你猜想cos(α-β)等于什么?cos(α-β)=cosαcosβ+sinαsinβks5u精品课件思考4:如图,设α,β为锐角,且α>β,角α的终边与单位圆的交点为P1, ∠P1OP=β,那么cos(α-β)表示哪条线段长?cos(α-β)=OMks5u精品课件思考5:如何用线段分别表示sinβ和cosβ?sinβcosβks5u精品课件思考6:cosαcosβ=OAcosα,它表示哪条线段长?
sinαsinβ=PAsinα,它表示哪条线段长?sinαsinβcosαcosβks5u精品课件思考7:利用OM=OB+BM=OB+CP可得什么结论?cos(α-β)=cosαcosβ+sinαsinβks5u精品课件xyPP1MBOAC+11ks5u精品课件思考8:上述推理能说明对任意角α,β,都有
cos(α-β)=cosαcosβ+sinαsinβ成立吗?思考9:根据cosαcosβ+sinαsinβ的结构特征,你能联想到一个相关计算原理吗?ks5u精品课件思考10:如图,设角α,β的终边与单位圆的交点分别为A、B,则向量 、
的坐标分别是什么?其数量积是什么?=(cosα,sinα)=(cosβ,sinβ)ks5u精品课件思考11:向量与的夹角θ与α、β有什么关系?根据数量积定义, 等于什么?由此可得什么结论? α=2kπ+β+θ或β=2kπ+α+θ cos(α-β)=cosαcosβ+sinαsinβks5u精品课件思考12:公式cos(α-β)=cosαcosβ+sinαsinβ称为差角的余弦公式,记作 ,该公式有什么特点?如何记忆?ks5u精品课件探究(二):两角差的余弦公式的变通 思考1:若已知α+β和β的三角函数值,如何求cosα的值? cosα=cos[(α+β)-β]= cos(α+β) cosβ+sin(α+β)sinβ. 思考2:利用α-(α-β)=β可得cosβ等于什么?cosβ=cos[(α-β)-α]= cos(α-β)cosα+sin(α-β)sinα.ks5u精品课件思考3:若cosα+cosβ=a,sinα+sinβ=b,则cos(α-β)等于什么?思考4:若cosα-cosβ=a,sinα-sinβ=b,则cos(α-β)等于什么?ks5u精品课件例1 利用余弦公式求cos15°的值. 例2 已知
β是第三象限角,求cos(α-β)的值.理论迁移例3 已知
且 , 求 的值. ks5u精品课件小结作业1.在差角的余弦公式的形成过程中,蕴涵着丰富的数学思想、方法和技巧,如数形结合,化归转换、归纳、猜想、构造、换元、向量等,我们要深刻理解和领会.2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.ks5u精品课件作业:
P127练习:1,2,3,4.3.在差角的余弦公式中,α,β既可以是单角,也可以是复角,运用时要注意角的变换,如,2β=(α+β)-(α-β) 等. 同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.
sinαsinβ=PAsinα,它表示哪条线段长?sinαsinβcosαcosβks5u精品课件思考7:利用OM=OB+BM=OB+CP可得什么结论?cos(α-β)=cosαcosβ+sinαsinβks5u精品课件xyPP1MBOAC+11ks5u精品课件思考8:上述推理能说明对任意角α,β,都有
cos(α-β)=cosαcosβ+sinαsinβ成立吗?思考9:根据cosαcosβ+sinαsinβ的结构特征,你能联想到一个相关计算原理吗?ks5u精品课件思考10:如图,设角α,β的终边与单位圆的交点分别为A、B,则向量 、
的坐标分别是什么?其数量积是什么?=(cosα,sinα)=(cosβ,sinβ)ks5u精品课件思考11:向量与的夹角θ与α、β有什么关系?根据数量积定义, 等于什么?由此可得什么结论? α=2kπ+β+θ或β=2kπ+α+θ cos(α-β)=cosαcosβ+sinαsinβks5u精品课件思考12:公式cos(α-β)=cosαcosβ+sinαsinβ称为差角的余弦公式,记作 ,该公式有什么特点?如何记忆?ks5u精品课件探究(二):两角差的余弦公式的变通 思考1:若已知α+β和β的三角函数值,如何求cosα的值? cosα=cos[(α+β)-β]= cos(α+β) cosβ+sin(α+β)sinβ. 思考2:利用α-(α-β)=β可得cosβ等于什么?cosβ=cos[(α-β)-α]= cos(α-β)cosα+sin(α-β)sinα.ks5u精品课件思考3:若cosα+cosβ=a,sinα+sinβ=b,则cos(α-β)等于什么?思考4:若cosα-cosβ=a,sinα-sinβ=b,则cos(α-β)等于什么?ks5u精品课件例1 利用余弦公式求cos15°的值. 例2 已知
β是第三象限角,求cos(α-β)的值.理论迁移例3 已知
且 , 求 的值. ks5u精品课件小结作业1.在差角的余弦公式的形成过程中,蕴涵着丰富的数学思想、方法和技巧,如数形结合,化归转换、归纳、猜想、构造、换元、向量等,我们要深刻理解和领会.2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.ks5u精品课件作业:
P127练习:1,2,3,4.3.在差角的余弦公式中,α,β既可以是单角,也可以是复角,运用时要注意角的变换,如,2β=(α+β)-(α-β) 等. 同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.
