2.7有理数的减法同步练习（1）

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
2.7有理数的减法
【同步达纲练习】
1．判断题
(1)如果a－b＝a，那么b＝0．
(2)如果a－b<0，那么a(3)如果a－b0．
(4)(－15)－(－8)＝(－15)＋(＋8)＝－23．
(5)|x－y|＝x－y．
(6)绝对值大于2而小于5的所有整数的和是0．
(7)若a>0，b<0，则a－b<0．
(8)－(－2)－|－2|<0．
(9)如果|a|＋|b|≠0，那么a、b不都为零．
(10)若a、b不全为零，那么|a＋b|>0．
2．填空题
(1)________－0＝－0．125． (2)(＋3)－ ________＝－1．
(3)_______－(－345)＝0． (4)0－________＝0．321．
(5)若－a>－|a|，则a的范围是________． (6)若a<0，则|a－|a||＝_______．
(7)若a、b互为相反数，则a＋b＝_____． (8)若a＋b>a－b，则b_______．
(9)若|a|－a＝b，则b________0(填>、<、≥或≤)．
(10)已知(a－b)2＋|b－1|＝0，则3a－2b＝___________．
3．选择题
(1)下列计算正确的是
A．7－(－7)＝0
B．0－3＝－3
C．
D．(－5)－(－6)＝－1
(2)如图2—11所示，a、b在数轴上的位置分别在原点的两旁，则|a－b|化简的结果是
A．a－b
B．b－a
C．－(a－b)
D．－(b－a)
图2—11
(3)如果a＋b＝c，且a＞c则
A．b一定是负数
B．a一定小于b
C．a一定是负数
D．b一定小于a
(4)如果｜a｜－｜b｜＝0，那么
A．a＝b
B．a、b互为相反数
C．a和b都是0
D．a＝b或a＝－b
(5)如果a的绝对值大于－5的绝对值，那么有
A．a>－5
B．a<－5
C．|a－(－5)|＝a－(－5)
D．以上均不对
(6)若3A．4
B．－4
C．10－2x
D．2x－10
(7)若a>0，b<0，|a|＝4，|b|＝a－2，则a－b的值是
A．2
B．－2
C．6
D．－6
(8)若有理数a满足＝1时，那么a是
A．正有理数
B．负有理数
C．非负有理数
D．非正有理数
4．计算下列各式的值：
(1)(－60)－(＋30)； (2)(－212)－(＋414)；
(3)0－(－101)； (4)(－)－(－)；
(5)(＋17)－(－30)； (6)(－)－(＋24)；
(7)(＋25)－(－0．25)； (8)(－65．3)－0；
(9)(＋12)－(＋15)； (10)(＋8．312)－(－11．688)；
(11)(－25．75)－(＋74．25)； (12)0－(＋375)；
(13)(－205)－0； (14)(－13)－(－31)．
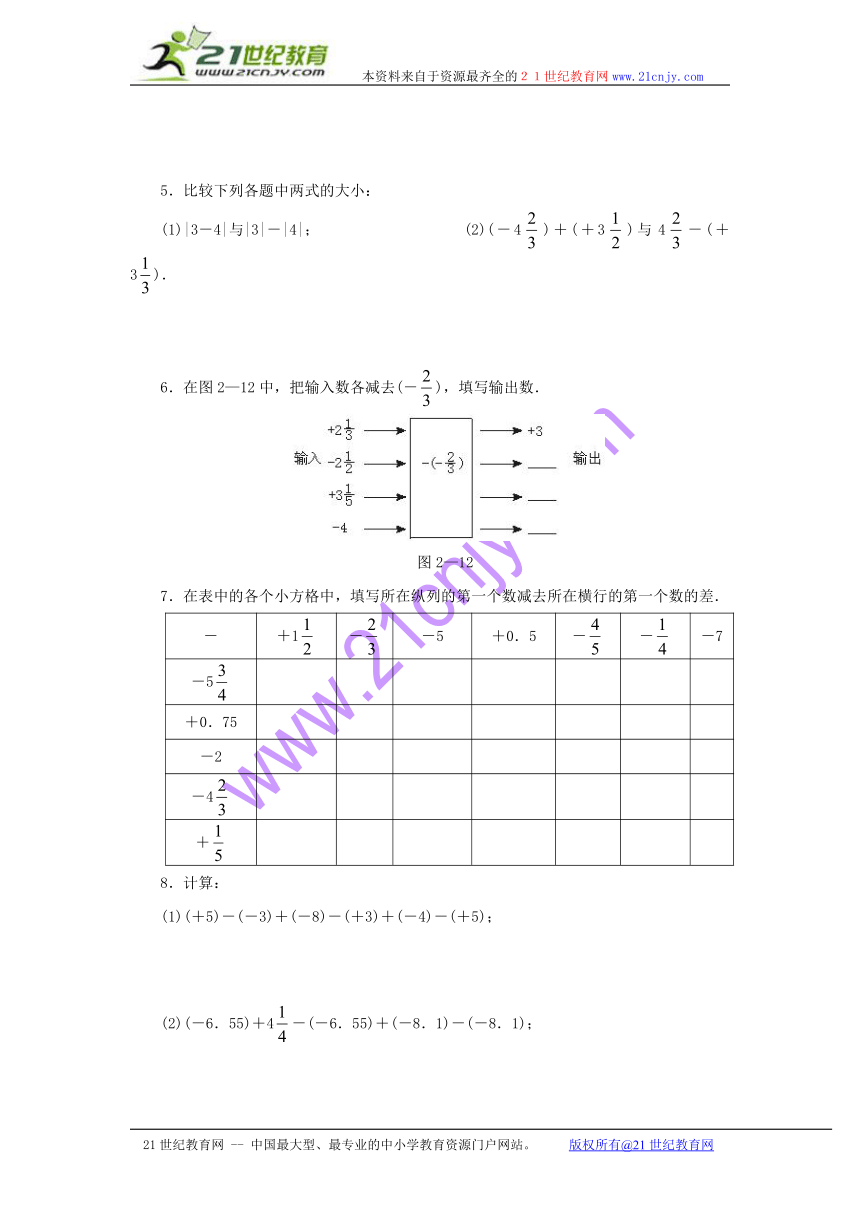
5．比较下列各题中两式的大小：
(1)|3－4|与|3|－|4|； (2)(－4)＋(＋3)与4－(＋3)．
6．在图2—12中，把输入数各减去(－)，填写输出数．
图2—12
7．在表中的各个小方格中，填写所在纵列的第一个数减去所在横行的第一个数的差．
－ ＋1 － －5 ＋0．5 － － －7
－5
＋0．75
－2
－4
＋
8．计算：
(1)(＋5)－(－3)＋(－8)－(＋3)＋(－4)－(＋5)；
(2)(－6．55)＋4－(－6．55)＋(－8．1)－(－8．1)；
(3)1＋；
(4)；
(5)(－8)＋(＋11)＋(－12)＋(＋39)；
(6)(＋5)＋(－9)＋(－91)＋(＋45)；
(7)(－5．4)＋(＋0．3)＋(－0．6)＋(＋0．7)；
(8)(－0．67)－(－0．01)－(－1．99)＋(＋0．67)；
(9)(－0．5)＋ (＋．
9．当a＝，b＝－，c＝－时，分别计算下列各式的值：
(1)a＋b； (2)a－b； (3)b－c；
(4)a＋(－c)； (5)a＋b－c； (6)a－b＋c．
10．已知a＝3，|b|＝4，求a＋b的值．
11．如果|a－2|＋|2b－5|＝0，求3a－2b的值．
【思路拓展题】
奇数与偶数的性质
偶数±偶数＝偶数；奇数±奇数＝偶数；
奇数±偶数＝奇数；奇数×奇数＝奇数；
奇数×偶数＝偶数；偶数×偶数＝偶数．
以上这些内容虽很简单，但在解决一些与奇偶数有关的问题时却有着举足轻重的作用．看下面的问题．你是否能够读懂？
设有n盏亮着的拉线开关，规定每次必须拉动n－1个拉线开关，试问：能否把所有的灯都关闭？证明你的结论或给出一种关灯的办法．
思路分析：从简单情况想起：当n＝1时，显然不行；当n＝2时，1号灯不动，2号关上，2号灯不动，1号关上，可行．当n＝3时，每盏灯拉动奇数次时才能关上，3个奇数的和仍为奇数，而n－1＝2，按规定总拉动开关的次数是偶数，因此不能把灯全部关闭，由此猜测当n为偶数时可以，当n为奇数时不行．
说明：(1)当n为奇数时，每盏灯拉动奇数次才能关闭，因此要把全部灯关闭，总拉动开关次数应是奇数个奇数的和，是奇数．但n－1是偶数，按规定只能拉动任意的偶数次开关，故无论如何不能把全部亮着的灯都关上．
(2)当n为偶数时，把n盏灯编序为1，2，3，…，n．仅需如下操作：
第一次：1号灯不动，拉动其余n－1个开关；
第二次：2号灯不动，拉动其余n－1个开关；
……
第n次：n号灯不动，拉动其余n－1个开关．
这样每盏灯拉动n－1次，即奇数次，因此可以用这种办法把全部亮着的灯关闭．你读懂了吗？
参考答案
【同步达纲练习】
1．(1)√　(2)√　(3)√　(4)×　(5)×　(6)√　(7)×　(8)×　(9)√　(10)×
2．(1)－0．125　(2)5　(3)－345　(4)－0．321
(5)a<0　(6)－2a　(7)0　(8)>0　(9)≥　(10)1
3．(1)B　(2)A　(3)A　(4)D　(5)D　(6)A　(7)C　(8)A
4．(1)－90　(2)－626　(3)101　(4)－　(5)47　(6)－24　(7)25　(8)－65．3
(9)－3　(10)20　(11)－100　(12)－375　(13)－205　(14)19
5．(1)>　(2)<
6．从上到下输出的数顺次是－1，3，－3．
7．
－7 －5 － －6 －4 －5 1
－ 1 5 1 1 7
－3 －1 3 －2 －1 －1 5
－6 －4 －5 －3 －4 2
－1 5 － 1 7
8．(1)－12　(2)4　(3)　(4)3　(5)30　(6)－50　(7)－5　(8)2　(9)4
9．(1)　(2)1　(3)　(4)　(5)　(6)　
10．7或－1　11．1
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网