算法的概念
图片预览






文档简介
课件22张PPT。1.1.1算法的概念古代算筹的功用大致和后来的算盘珠相仿.五以下数用几根筹表示几,6、7、8、9四个数目,用一根筹放在上边表示五,余下来每一根筹表示一,放在下边,用算筹表示数目时有纵、横两种方式.我国是算盘的故乡,在计算机普遍使用的的今天,古老的算盘不但没有被废弃,反而因为它的方便、灵活的特点,在许多国家方兴未艾。 计算机的问世可谓20世纪最伟大的发明,它把人类社会带进了信息技术时代,而算法是计算机科学的重要基础,就像使用算盘一样,人们需要给计算机编制“口诀”——算法,才能让它工作,要想了解计算机的工作原理,算法的学习是一个开始。问1、要把水果装入冰箱分几步?引入问2、 求1×2×3×4×5的步骤。步骤1:先求1×2,得到结果2;
步骤2:将步骤1得到的结果2再乘以3,得到6;
步骤3:将步骤2得到的结果6再乘以4,得到结果24;
步骤4:将步骤3得到的结果24再乘以5,得到120。
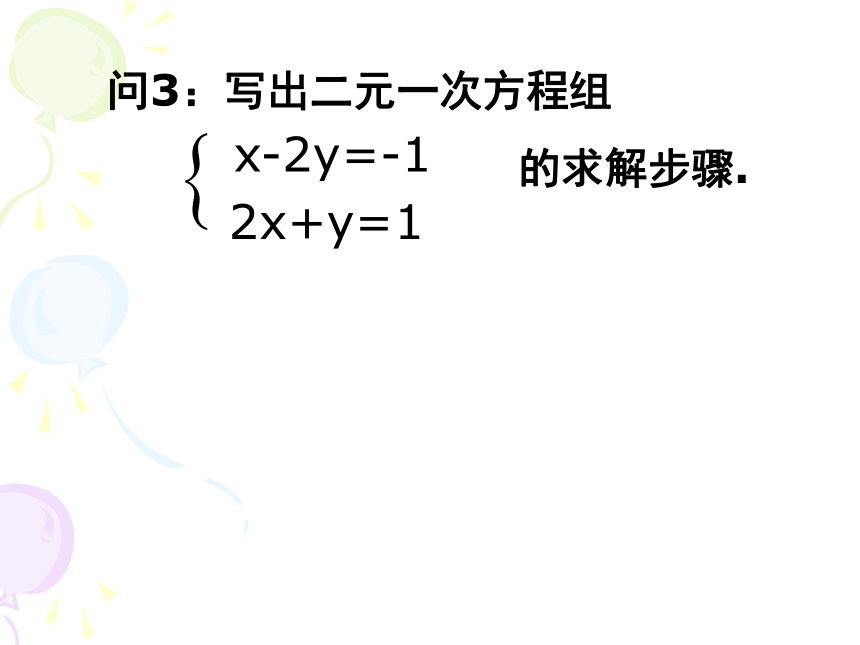
问3:写出二元一次方程组
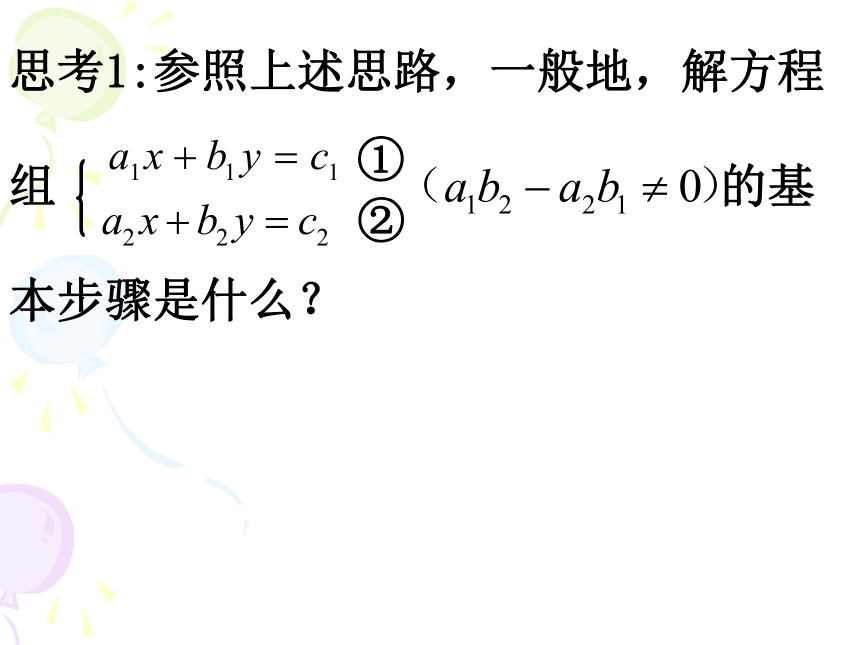
的求解步骤. x-2y=-1 2x+y=1算法过程: 要能一步一步执行,每一步执行的操作,必须确切,不能含混不清楚,而且经过有限步后能得出结果。算法的含义:
在数学中,按照一定规则解决某一类问题的明确和有限的步骤称为算法。
归纳与总结明辨定义
有人对哥德巴赫猜想“任何大于4的偶数都能写成两个质数之和”设计了如下操作步骤:
第一步,检验6=3+3, 第二步,检验8=3+5, 第三步,检验10=5+5,……
利用计算机无穷地进行下去!
请问:这是一个算法吗? 算法的特征 有穷性: 一个算法应包含有限的操作步骤而不能是
无限的。 确定性: 算法中每一个步骤应当是确定的,而不能应 当是含糊的、模棱两可的。有效性: 算法中每一个步骤应当能有效地执行,并得到
确定的结果。知识探究:算法的步骤设计例1:如果让计算机判断7是否为质数,如何设计算法步骤? 第一步,用2除7,得到余数1,所以2不能整除7.第四步,用5除7,得到余数2,所以5不能整除7. 第五步,用6除7,得到余数1,所以6不能整除7. 第二步,用3除7,得到余数1,所以3不能整除7.第三步,用4除7,得到余数3,所以4不能整除7. 因此,7是质数.变式:整数89是否为质数?如果让计算机判断89是否为质数,按照上述算法需要设计多少个步骤? 第一步,用2除89,得到余数1,所以2不能整除89.第二步,用3除89,得到余数2,所以3不能整除89.第三步,用4除89,得到余数1,所以4不能整除89. …… …… …… ……
第八十七步,用88除89,得到余数1,所以88不能 整除89.因此,89是质数. 用2~88逐一去除89求余数,需要87个步骤,这些步骤基本是重复操作,我们可以按下面的思路改进这个算法,减少算法的步骤.(1)用i表示2~88中的任意一个整数,并从2开始取数;(2)用i除89,得到余数r. 若r=0,则89不是质数;若r≠0,将i用i+1替代,再执行同样的操作; (3)这个操作一直进行到i取88为止.你能按照这个思路,设计一个“判断89是否为质数”的算法步骤吗?用i除89,得到余数r; 令i=2; 若r=0,则89不是质数,结束算法;若r≠0,将i的值增加1,仍用i表示; 判断“i>88”是否成立?若是,则89是质数,结束算法;否则,返回第二步. 第一步, 第四步, 第三步, 第二步, 算法设计:思考:任意给定一个大于1的整数n,试设计一个算法对n是否为质数作出判定。施展才华小结:本节课主要讲了算法的概念,算法就是解决问题的步骤,平时无论我们做什么事都离不开算法,算法的描述可以用自然语言,也可以用数学语言。 一位商人有9枚银元,其中有1枚略轻的是假银元。你能用天平(无砝码)将假银元找出来吗?写出解决这一问题的一种算法。施展才华一个大人和两个小孩一起渡河,渡口只有一条小船,每次只能渡1个大人或两个小孩,他们三人都会划船,但都不会游泳。试问他们怎样渡过河去?请写出一个渡河方案。
第一步,两个小孩同船过河去;
第二步,一个小孩划船回来;
第三步,一个大人划船过河去;
第四步,对岸的小孩划船回来;
第五步,两个小孩同船渡过河去。思考2: 练习写出解一元二次方程的一个算法。
2.写出求1至1000的正整数中3的倍数的一个算法。作业 设计一个计算 的值的算法。(用数学语言)注意算法的要求;
理解循环算法。怎样用数学语言表示循环?再见
步骤2:将步骤1得到的结果2再乘以3,得到6;
步骤3:将步骤2得到的结果6再乘以4,得到结果24;
步骤4:将步骤3得到的结果24再乘以5,得到120。
问3:写出二元一次方程组
的求解步骤. x-2y=-1 2x+y=1算法过程: 要能一步一步执行,每一步执行的操作,必须确切,不能含混不清楚,而且经过有限步后能得出结果。算法的含义:
在数学中,按照一定规则解决某一类问题的明确和有限的步骤称为算法。
归纳与总结明辨定义
有人对哥德巴赫猜想“任何大于4的偶数都能写成两个质数之和”设计了如下操作步骤:
第一步,检验6=3+3, 第二步,检验8=3+5, 第三步,检验10=5+5,……
利用计算机无穷地进行下去!
请问:这是一个算法吗? 算法的特征 有穷性: 一个算法应包含有限的操作步骤而不能是
无限的。 确定性: 算法中每一个步骤应当是确定的,而不能应 当是含糊的、模棱两可的。有效性: 算法中每一个步骤应当能有效地执行,并得到
确定的结果。知识探究:算法的步骤设计例1:如果让计算机判断7是否为质数,如何设计算法步骤? 第一步,用2除7,得到余数1,所以2不能整除7.第四步,用5除7,得到余数2,所以5不能整除7. 第五步,用6除7,得到余数1,所以6不能整除7. 第二步,用3除7,得到余数1,所以3不能整除7.第三步,用4除7,得到余数3,所以4不能整除7. 因此,7是质数.变式:整数89是否为质数?如果让计算机判断89是否为质数,按照上述算法需要设计多少个步骤? 第一步,用2除89,得到余数1,所以2不能整除89.第二步,用3除89,得到余数2,所以3不能整除89.第三步,用4除89,得到余数1,所以4不能整除89. …… …… …… ……
第八十七步,用88除89,得到余数1,所以88不能 整除89.因此,89是质数. 用2~88逐一去除89求余数,需要87个步骤,这些步骤基本是重复操作,我们可以按下面的思路改进这个算法,减少算法的步骤.(1)用i表示2~88中的任意一个整数,并从2开始取数;(2)用i除89,得到余数r. 若r=0,则89不是质数;若r≠0,将i用i+1替代,再执行同样的操作; (3)这个操作一直进行到i取88为止.你能按照这个思路,设计一个“判断89是否为质数”的算法步骤吗?用i除89,得到余数r; 令i=2; 若r=0,则89不是质数,结束算法;若r≠0,将i的值增加1,仍用i表示; 判断“i>88”是否成立?若是,则89是质数,结束算法;否则,返回第二步. 第一步, 第四步, 第三步, 第二步, 算法设计:思考:任意给定一个大于1的整数n,试设计一个算法对n是否为质数作出判定。施展才华小结:本节课主要讲了算法的概念,算法就是解决问题的步骤,平时无论我们做什么事都离不开算法,算法的描述可以用自然语言,也可以用数学语言。 一位商人有9枚银元,其中有1枚略轻的是假银元。你能用天平(无砝码)将假银元找出来吗?写出解决这一问题的一种算法。施展才华一个大人和两个小孩一起渡河,渡口只有一条小船,每次只能渡1个大人或两个小孩,他们三人都会划船,但都不会游泳。试问他们怎样渡过河去?请写出一个渡河方案。
第一步,两个小孩同船过河去;
第二步,一个小孩划船回来;
第三步,一个大人划船过河去;
第四步,对岸的小孩划船回来;
第五步,两个小孩同船渡过河去。思考2: 练习写出解一元二次方程的一个算法。
2.写出求1至1000的正整数中3的倍数的一个算法。作业 设计一个计算 的值的算法。(用数学语言)注意算法的要求;
理解循环算法。怎样用数学语言表示循环?再见
