(新人教b版必修4)数学:1.2.2《单位圆与三角函数线》课件
文档属性
| 名称 | (新人教b版必修4)数学:1.2.2《单位圆与三角函数线》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 91.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-16 19:20:00 | ||
图片预览





文档简介
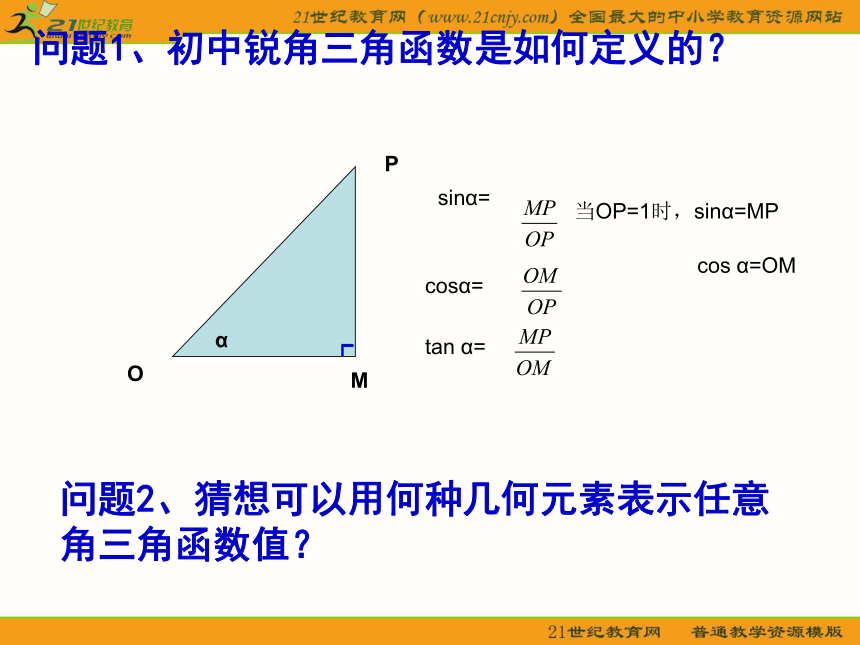
课件17张PPT。三角函数线问题2、猜想可以用何种几何元素表示任意角三角函数值?问题1、初中锐角三角函数是如何定义的?
OMPα sinα=cosα=tan α=当OP=1时,sinα=MP
cos α=OM
┍设P(x,y)是α终边上任一点,线段0P的长度为 r复习:任意角三角函数的定义①比值 叫做 的正弦,
记作 ,即 .②比值 叫做 的余弦,
记作 ,即 .③比值 叫做 的正切,
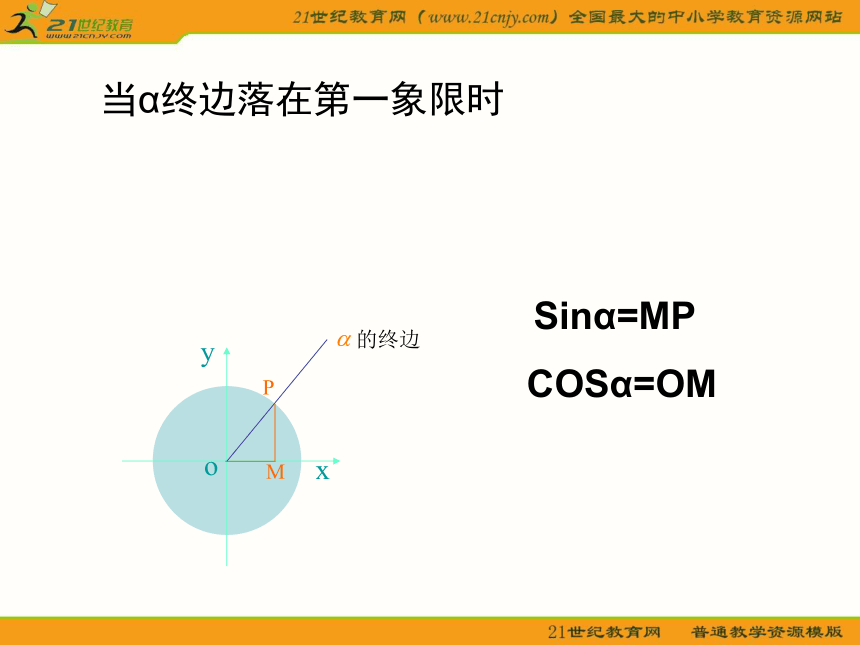
记作 ,即 .x 角α的终边结论:当P点在以原点为圆心,半径为1的圆(称为单位圆)上时, r=1,而,sinα,cosα的函数值分别为点P的纵坐标y和横坐标x。当α终边落在第一象限时MP(x,y)
1当α终边落在第二象限时
MP(x,y)
1当α终边落在第一象限时MPSinα=MPCOSα=OM当α终边落在第二象限时
MPSinα=MPCOSα=OM
有向线段MP的数量等于角的正弦,把有向线段MP叫做正弦线有向线段OM的数量等于角的余弦,把有向线段OM叫做余弦线
定义介绍:正切线如何画?AT当α终边落在第一象限时
tanα=AT1探究活动:当α终边落在第二象限时PATtanα=AT
有向线段AT叫做正切线1PMAT步骤:1、作直角坐标系和角的终边2、作单位圆,圆与角的终边的交点为P,与 x轴正半轴交点为A3、过P点作 x轴的垂线,垂足为M4、过A点作 x 轴的垂线,与角的终边或其反向延长线交于T点5、有向线段MP、OM、AT就为所求归纳1:凡含有原点的线段,均以原点为起点2:不含原点的线段,均以此线段与坐标轴的公共点为起点 当α终边落在坐标轴上时,情况又如何?α终边落在x轴上时,正弦线、正切线分别变成一个点, α终边落在y轴上时,余弦线变成一个点,正切线不存在练习: 作出下列各角的正弦线,余弦线,正切线.(1) ;(2) .比较下列各组数的大小Sin1和 sincos 和 cos练习2
1、用字母表示有向线段时,要分清起点和终点,书写顺序要准确2三角函数线凡含有原点的线段,均以原点为
起点不含原点的线段,均以此线段与坐标轴的公共点为起点
3、α终边落在x轴上时,正弦线、正切线分别变成一个点, α终边落在y轴上时,余弦线变成一个点,正切线不存在
回顾小结:
OMPα sinα=cosα=tan α=当OP=1时,sinα=MP
cos α=OM
┍设P(x,y)是α终边上任一点,线段0P的长度为 r复习:任意角三角函数的定义①比值 叫做 的正弦,
记作 ,即 .②比值 叫做 的余弦,
记作 ,即 .③比值 叫做 的正切,
记作 ,即 .x 角α的终边结论:当P点在以原点为圆心,半径为1的圆(称为单位圆)上时, r=1,而,sinα,cosα的函数值分别为点P的纵坐标y和横坐标x。当α终边落在第一象限时MP(x,y)
1当α终边落在第二象限时
MP(x,y)
1当α终边落在第一象限时MPSinα=MPCOSα=OM当α终边落在第二象限时
MPSinα=MPCOSα=OM
有向线段MP的数量等于角的正弦,把有向线段MP叫做正弦线有向线段OM的数量等于角的余弦,把有向线段OM叫做余弦线
定义介绍:正切线如何画?AT当α终边落在第一象限时
tanα=AT1探究活动:当α终边落在第二象限时PATtanα=AT
有向线段AT叫做正切线1PMAT步骤:1、作直角坐标系和角的终边2、作单位圆,圆与角的终边的交点为P,与 x轴正半轴交点为A3、过P点作 x轴的垂线,垂足为M4、过A点作 x 轴的垂线,与角的终边或其反向延长线交于T点5、有向线段MP、OM、AT就为所求归纳1:凡含有原点的线段,均以原点为起点2:不含原点的线段,均以此线段与坐标轴的公共点为起点 当α终边落在坐标轴上时,情况又如何?α终边落在x轴上时,正弦线、正切线分别变成一个点, α终边落在y轴上时,余弦线变成一个点,正切线不存在练习: 作出下列各角的正弦线,余弦线,正切线.(1) ;(2) .比较下列各组数的大小Sin1和 sincos 和 cos练习2
1、用字母表示有向线段时,要分清起点和终点,书写顺序要准确2三角函数线凡含有原点的线段,均以原点为
起点不含原点的线段,均以此线段与坐标轴的公共点为起点
3、α终边落在x轴上时,正弦线、正切线分别变成一个点, α终边落在y轴上时,余弦线变成一个点,正切线不存在
回顾小结:
