(新人教b版必修4)数学:1.3.2《余弦函数、正切函数的图像与性质》课件
文档属性
| 名称 | (新人教b版必修4)数学:1.3.2《余弦函数、正切函数的图像与性质》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 67.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-16 00:00:00 | ||
图片预览




文档简介
课件11张PPT。余弦函数的图象与性质 学习目标
1.通过本节学习,应掌握余弦函数图象的画法.
2.会用“五点法”画出余弦曲线简图.
3.能结合余弦函数图象理解余弦函数的性质(定义域、值域、周期性、奇偶性、单调性)
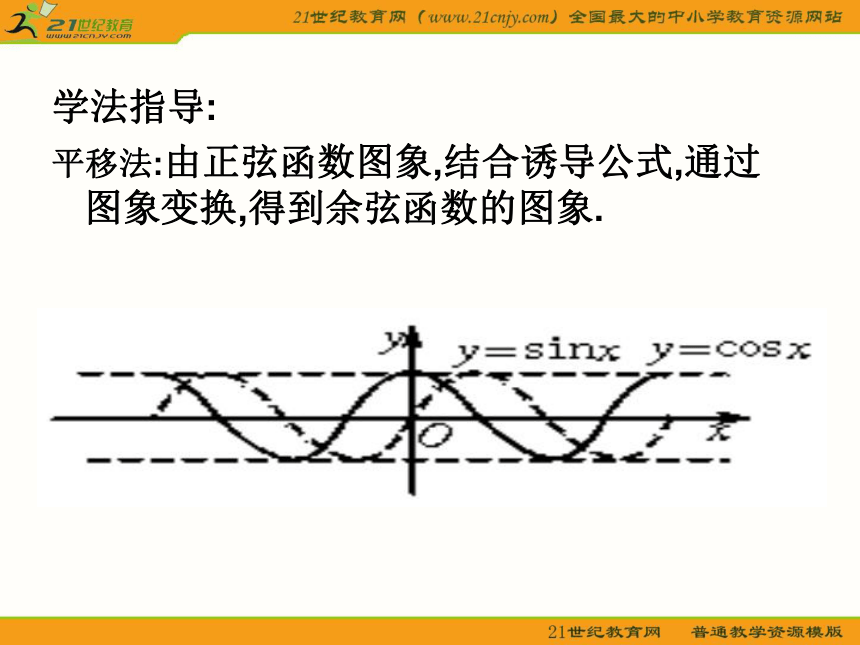
学法指导:
平移法:由正弦函数图象,结合诱导公式,通过图象变换,得到余弦函数的图象.学法指导:
1.根据图象分析性质,找出关键点,并总结“五点法”作图方法;五点法:五个点是
仿正弦函数探讨余弦函数的性质.
2.应用“五点法”作与正弦、余弦函数有关的函数的图象(如y=1+sinx,y=2cosx的图象)
学法指导:
1. 余弦曲线是中心对称图形,其所有的对称中心坐标是_____________;
2.余弦曲线是轴对称图形,其所有的对称轴方程是_______________.
余弦曲线的对称轴一定是过余弦曲线的最高点或最低点,此时余弦值为最大值或最小值.余弦函数的性质
1.定义域:余弦函数的定义域是实数集R.
2.值域:[-1,1],即-1≤cosx≤1. 当且仅当
x=________时,余弦函数y=cosx取得最大值1.
当且仅当x=____________时,余弦函数y=cosx取得
最小值-1.
3.周期:2π
4.奇偶性:由诱导公式cos(-x)=cosx可知,余弦函数是偶函数,它的图象关于y轴对称.
5.单调性:余弦函数y=cosx在每个闭区间_______________上,都是减函数;y=cosx在每个闭区间____________________上都是增函数.余弦型函数 的
定义域R;值域[-A,A];周期
当 时 为偶函数,
当 时 为奇函数;对称轴由 求得
对称中心横坐标由 求得.
其单调区间求法与正弦型函数相同。学习时应注意的问题
1.会说明和判断余弦函数的奇偶性.
2.能说明余弦函数的单调性和单调区间.
3.掌握余弦型函数
的周期性及求法.课堂练习一
1.求使下列函数取得最小值的自变量x的集合,并写出最小值是什么.
①y=-2sinx,x∈R ; ②y=2-cos2x ,x∈R.
2.求下列函数的周期:
①y=sin3x,x∈R;②y=cos(5x+1),x∈R.
3.已知函数f(x)=(sinx+cosx)-|sinx-cosx|
则f(x)的值域是_______
课堂练习二
1.判断下列函数的奇偶性
(1)f(x)=|x|+cosx;
(2)f(x)=sinx+cosx;
(3)f(x)=cosx|sinx|+sinx|cosx|.
2.已知f(x)是定义在R上的奇函数,
且x>0时, f(x)=sinx+cosx,则在定义域R上,f(x)=___________.
3.已知函数y=a-bcos3x的最大值为6,最小值为-2,求a,b的值.
4.求y=cos2x的单调区间.
5.教材56页-4,5.
1.通过本节学习,应掌握余弦函数图象的画法.
2.会用“五点法”画出余弦曲线简图.
3.能结合余弦函数图象理解余弦函数的性质(定义域、值域、周期性、奇偶性、单调性)
小结
1.通过本节学习,应掌握余弦函数图象的画法.
2.会用“五点法”画出余弦曲线简图.
3.能结合余弦函数图象理解余弦函数的性质(定义域、值域、周期性、奇偶性、单调性)
学法指导:
平移法:由正弦函数图象,结合诱导公式,通过图象变换,得到余弦函数的图象.学法指导:
1.根据图象分析性质,找出关键点,并总结“五点法”作图方法;五点法:五个点是
仿正弦函数探讨余弦函数的性质.
2.应用“五点法”作与正弦、余弦函数有关的函数的图象(如y=1+sinx,y=2cosx的图象)
学法指导:
1. 余弦曲线是中心对称图形,其所有的对称中心坐标是_____________;
2.余弦曲线是轴对称图形,其所有的对称轴方程是_______________.
余弦曲线的对称轴一定是过余弦曲线的最高点或最低点,此时余弦值为最大值或最小值.余弦函数的性质
1.定义域:余弦函数的定义域是实数集R.
2.值域:[-1,1],即-1≤cosx≤1. 当且仅当
x=________时,余弦函数y=cosx取得最大值1.
当且仅当x=____________时,余弦函数y=cosx取得
最小值-1.
3.周期:2π
4.奇偶性:由诱导公式cos(-x)=cosx可知,余弦函数是偶函数,它的图象关于y轴对称.
5.单调性:余弦函数y=cosx在每个闭区间_______________上,都是减函数;y=cosx在每个闭区间____________________上都是增函数.余弦型函数 的
定义域R;值域[-A,A];周期
当 时 为偶函数,
当 时 为奇函数;对称轴由 求得
对称中心横坐标由 求得.
其单调区间求法与正弦型函数相同。学习时应注意的问题
1.会说明和判断余弦函数的奇偶性.
2.能说明余弦函数的单调性和单调区间.
3.掌握余弦型函数
的周期性及求法.课堂练习一
1.求使下列函数取得最小值的自变量x的集合,并写出最小值是什么.
①y=-2sinx,x∈R ; ②y=2-cos2x ,x∈R.
2.求下列函数的周期:
①y=sin3x,x∈R;②y=cos(5x+1),x∈R.
3.已知函数f(x)=(sinx+cosx)-|sinx-cosx|
则f(x)的值域是_______
课堂练习二
1.判断下列函数的奇偶性
(1)f(x)=|x|+cosx;
(2)f(x)=sinx+cosx;
(3)f(x)=cosx|sinx|+sinx|cosx|.
2.已知f(x)是定义在R上的奇函数,
且x>0时, f(x)=sinx+cosx,则在定义域R上,f(x)=___________.
3.已知函数y=a-bcos3x的最大值为6,最小值为-2,求a,b的值.
4.求y=cos2x的单调区间.
5.教材56页-4,5.
1.通过本节学习,应掌握余弦函数图象的画法.
2.会用“五点法”画出余弦曲线简图.
3.能结合余弦函数图象理解余弦函数的性质(定义域、值域、周期性、奇偶性、单调性)
小结
