(新人教b版必修4)数学:1.3.1《三角函数的图象与性质》教案2
文档属性
| 名称 | (新人教b版必修4)数学:1.3.1《三角函数的图象与性质》教案2 |

|
|
| 格式 | rar | ||
| 文件大小 | 75.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-16 19:20:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.3.1正弦函数的图象与性质(2)
教学目标:
1.知识与技能
(1)理解正弦函数的性质
(2)理解周期函数与最小正周期的意义
2.过程与方法
通过正弦函数的图像,进一步体会数形结合的思想方法。
3.情感、态度与价值观
通过正弦函数性质的学习,培养学生 “看图说话”的能力,即图形语言、文字语言与符号语言的转换,从而达到从直观到抽象的飞跃。
教学重点:正弦函数的性质
教学难点:正弦函数的周期性
教学方法:引导学生正弦函数的图像,观察、归纳、启发探究相结合的教学方法,运用现代化多媒体教学手段,进行教学活动。首先由形及数,数形结合,通过设置问题引导学生观察、分析、归纳正弦函数的性质,使学生在独立思考的基础上进行合作交流,在思考、探究和交流的过程中获得对正弦函数的性质的全面的理解与认识。
教学过程:
教学环节 教学内容 师生互动 设计意图
复习引入 复习的图像函数的性质有哪些? 教师提出问题,学生回答。 为学生认识函数的性质作好准备。
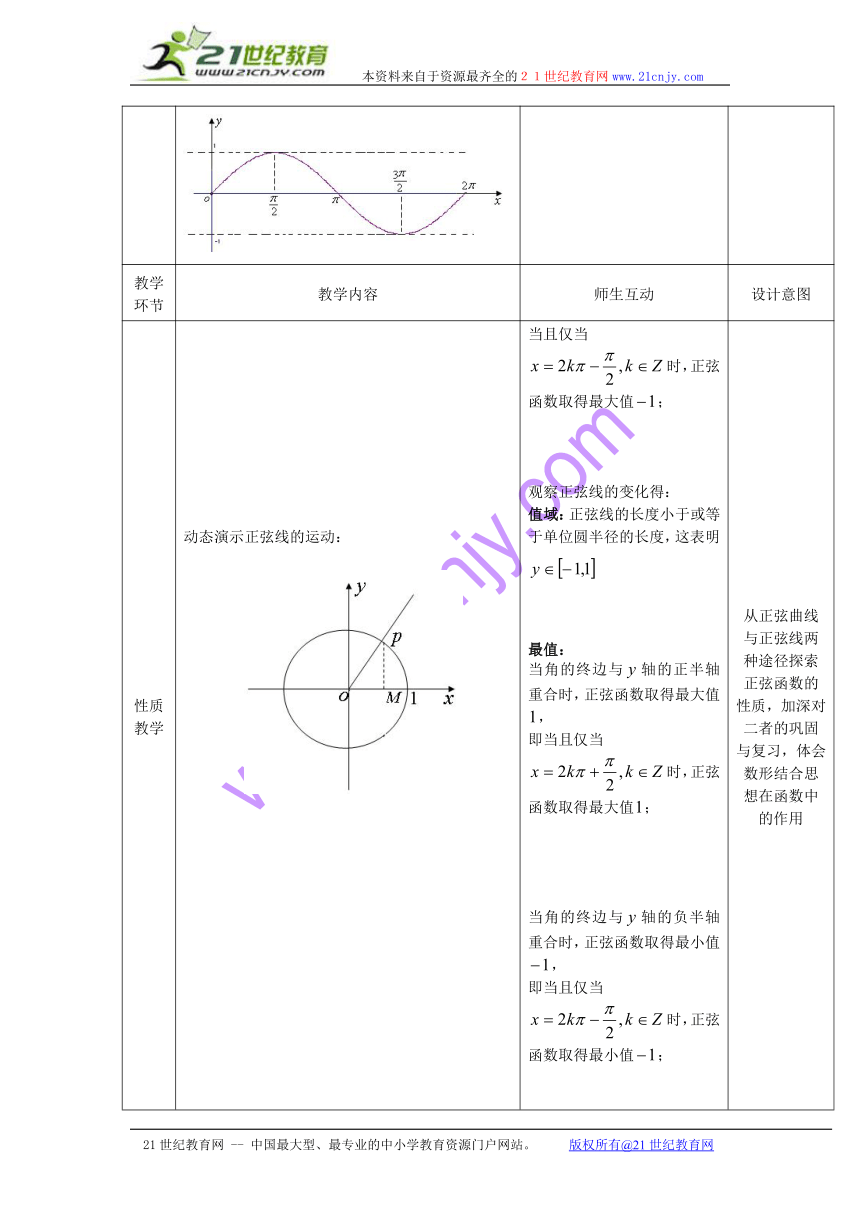
性质教学 正弦函数的值域与最值正弦函数的图像 值域:观察正弦曲线分布在两条平行直线和之间,这表明最值:当且仅当时,正弦函数取得最大值;
教学环节 教学内容 师生互动 设计意图
性质教学 动态演示正弦线的运动:21世纪教育网 当且仅当时,正弦函数取得最大值;观察正弦线的变化得:值域:正弦线的长度小于或等于单位圆半径的长度,这表明最值:当角的终边与轴的正半轴重合时,正弦函数取得最大值,即当且仅当时,正弦函数取得最大值;当角的终边与轴的负半轴重合时,正弦函数取得最小值,即当且仅当时,正弦函数取得最小值; 从正弦曲线与正弦线两种途径探索正弦函数的性质,加深对二者的巩固与复习,体会数形结合思想在函数中的作用
教学环节 教学内容 师生互动 设计意图
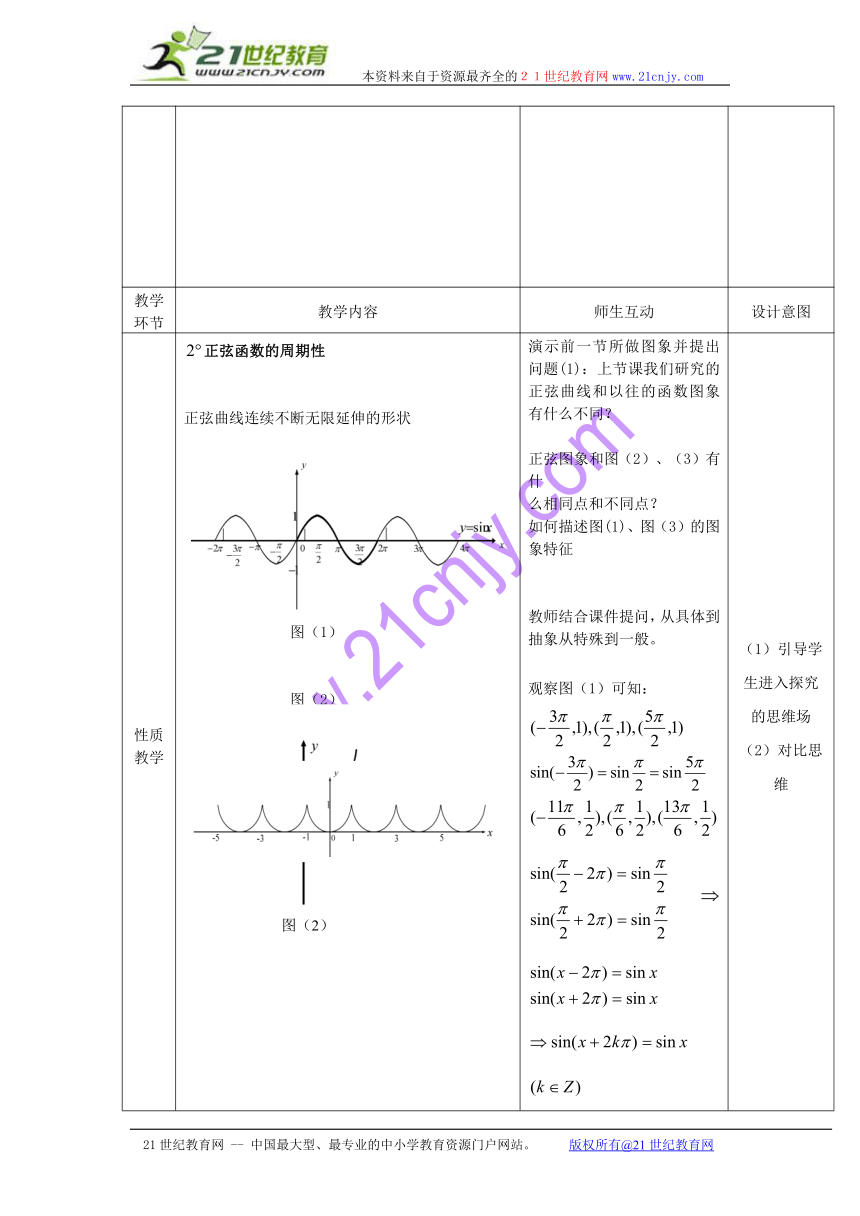
性质教学 正弦函数的周期性正弦曲线连续不断无限延伸的形状图(1)图(2)图(3) 演示前一节所做图象并提出问题(1):上节课我们研究的正弦曲线和以往的函数图象有什么不同?正弦图象和图(2)、(3)有什么相同点和不同点?如何描述图(1)、图(3)的图象特征教师结合课件提问,从具体到抽象从特殊到一般。观察图(1)可知:观察图(3)可知: (1)引导学生进入探究的思维场(2)对比思维
教学环节 教学内容 师生互动 设计意图
性质教学 定义:对于函数,如果存在一个非零常数,使得定义域内的每一个值,都满足,那么函数就叫做周期函数,非零常数叫做这个函数的周期. 对于一个周期函数,如果在它的所有周期中存在一个最小的正数,那么这个最小正数就叫做它的最小正周期.说明:正弦函数是一个周期函数,都是它的周期,是其最小正周期 由图(2)的分析可知:当自变量的值每增加或减少的整数倍时,正弦函数的值重复出现.在单位圆中,当角的终边绕原点转动回到原处时,正弦线的数量(长度和符号)不发生变化。师生共同总结函数周期性的定义。 从感性认识向理性认识从过渡最后抽象概括并渗透三种语言的转化
性质教学 正弦函数的奇偶性 教师提出问题:1.如何判断函数的奇偶性?[来源:21世纪教育网]2.正弦函数具有奇偶性吗?21世纪教育网3.如何判断它的奇偶性?学生回答:1.偶函数图像关于轴对称;奇函数图像关于成中心对称。 21世纪教育网
教学环节 教学内容 师生互动 设计意图
性质教学 正弦函数的图像 正弦函数的单调性正弦函数的一个周期内的图像中,如图: 正弦函数具有奇偶性。方法一:由诱导公式可知,正弦函数是奇函数。方法二:正弦函数的图像关于原点成中心对称可知,正弦函数是奇函数。方法三:由正弦线知,角的正弦线知,,故正弦函数是奇函数。教师引导学生观察正弦曲线在一个周期的图像,可以看出:当由增加到时,由增加到;当由增加到时,由减小到。教师根据学生的回答,得出左边的表格,直观体现变化趋势。 教师引导学生从诱导公式、正弦曲线、正弦线三种角度探究正弦函数的奇偶性,温故知新。从正弦曲线及正弦线双重角度体会正弦函数的单调性,进一步体会三角函数线及正弦曲线的工具性。
教学环节 教学内容 师生互动 设计意图
性质教学 动态演示正弦线的运动: 随着正弦线的变化,体会正弦函数的单调性。学生总结正弦函数的单调性:单调递增区间:单调递减区间:
应用举例 例1.设,求的取值范围。例2.求使下列函数取得最大值和最小值的的取值范围,并说出最大值和最小值是什么:(1)(2)(3)例3.求下列函数的周期(1)(2)例4.不通过求值,指出下列各式大于零还是小于零:(1);(2) 师:例1中体现出什么基础知识?例2(1)中体现什么基本方法?例2(2)中为什么与同时取得最大值?例2(3)通过观察题目结构可以利用什么方法转化成什么问题?例3 基本三角函数的最小正周期是什么?怎样利用换元法解决(1)(2)的周期?对一般的函数如何求出周期? 使学生巩固掌握正弦函数的性质。从特殊到一般,类比思维
归纳小结 1.知识:正弦函数的性质。2.思想方法:数形结合思想、换元法、类比法。 学生反思本节内容,对知识进行总结,教师对思想方法进行提炼。 让学生学会学习,学会总结。
布置作业 层次1:43页A中3、5;B中3。层次2:43页A中4。 层次1要求所有学生完成;层次2要求中等以上水平完成。 使学生进一步巩固和应用所学知识。
w.w.w.k.s.5.u.c.o.m
www.
图(2)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
1.3.1正弦函数的图象与性质(2)
教学目标:
1.知识与技能
(1)理解正弦函数的性质
(2)理解周期函数与最小正周期的意义
2.过程与方法
通过正弦函数的图像,进一步体会数形结合的思想方法。
3.情感、态度与价值观
通过正弦函数性质的学习,培养学生 “看图说话”的能力,即图形语言、文字语言与符号语言的转换,从而达到从直观到抽象的飞跃。
教学重点:正弦函数的性质
教学难点:正弦函数的周期性
教学方法:引导学生正弦函数的图像,观察、归纳、启发探究相结合的教学方法,运用现代化多媒体教学手段,进行教学活动。首先由形及数,数形结合,通过设置问题引导学生观察、分析、归纳正弦函数的性质,使学生在独立思考的基础上进行合作交流,在思考、探究和交流的过程中获得对正弦函数的性质的全面的理解与认识。
教学过程:
教学环节 教学内容 师生互动 设计意图
复习引入 复习的图像函数的性质有哪些? 教师提出问题,学生回答。 为学生认识函数的性质作好准备。
性质教学 正弦函数的值域与最值正弦函数的图像 值域:观察正弦曲线分布在两条平行直线和之间,这表明最值:当且仅当时,正弦函数取得最大值;
教学环节 教学内容 师生互动 设计意图
性质教学 动态演示正弦线的运动:21世纪教育网 当且仅当时,正弦函数取得最大值;观察正弦线的变化得:值域:正弦线的长度小于或等于单位圆半径的长度,这表明最值:当角的终边与轴的正半轴重合时,正弦函数取得最大值,即当且仅当时,正弦函数取得最大值;当角的终边与轴的负半轴重合时,正弦函数取得最小值,即当且仅当时,正弦函数取得最小值; 从正弦曲线与正弦线两种途径探索正弦函数的性质,加深对二者的巩固与复习,体会数形结合思想在函数中的作用
教学环节 教学内容 师生互动 设计意图
性质教学 正弦函数的周期性正弦曲线连续不断无限延伸的形状图(1)图(2)图(3) 演示前一节所做图象并提出问题(1):上节课我们研究的正弦曲线和以往的函数图象有什么不同?正弦图象和图(2)、(3)有什么相同点和不同点?如何描述图(1)、图(3)的图象特征教师结合课件提问,从具体到抽象从特殊到一般。观察图(1)可知:观察图(3)可知: (1)引导学生进入探究的思维场(2)对比思维
教学环节 教学内容 师生互动 设计意图
性质教学 定义:对于函数,如果存在一个非零常数,使得定义域内的每一个值,都满足,那么函数就叫做周期函数,非零常数叫做这个函数的周期. 对于一个周期函数,如果在它的所有周期中存在一个最小的正数,那么这个最小正数就叫做它的最小正周期.说明:正弦函数是一个周期函数,都是它的周期,是其最小正周期 由图(2)的分析可知:当自变量的值每增加或减少的整数倍时,正弦函数的值重复出现.在单位圆中,当角的终边绕原点转动回到原处时,正弦线的数量(长度和符号)不发生变化。师生共同总结函数周期性的定义。 从感性认识向理性认识从过渡最后抽象概括并渗透三种语言的转化
性质教学 正弦函数的奇偶性 教师提出问题:1.如何判断函数的奇偶性?[来源:21世纪教育网]2.正弦函数具有奇偶性吗?21世纪教育网3.如何判断它的奇偶性?学生回答:1.偶函数图像关于轴对称;奇函数图像关于成中心对称。 21世纪教育网
教学环节 教学内容 师生互动 设计意图
性质教学 正弦函数的图像 正弦函数的单调性正弦函数的一个周期内的图像中,如图: 正弦函数具有奇偶性。方法一:由诱导公式可知,正弦函数是奇函数。方法二:正弦函数的图像关于原点成中心对称可知,正弦函数是奇函数。方法三:由正弦线知,角的正弦线知,,故正弦函数是奇函数。教师引导学生观察正弦曲线在一个周期的图像,可以看出:当由增加到时,由增加到;当由增加到时,由减小到。教师根据学生的回答,得出左边的表格,直观体现变化趋势。 教师引导学生从诱导公式、正弦曲线、正弦线三种角度探究正弦函数的奇偶性,温故知新。从正弦曲线及正弦线双重角度体会正弦函数的单调性,进一步体会三角函数线及正弦曲线的工具性。
教学环节 教学内容 师生互动 设计意图
性质教学 动态演示正弦线的运动: 随着正弦线的变化,体会正弦函数的单调性。学生总结正弦函数的单调性:单调递增区间:单调递减区间:
应用举例 例1.设,求的取值范围。例2.求使下列函数取得最大值和最小值的的取值范围,并说出最大值和最小值是什么:(1)(2)(3)例3.求下列函数的周期(1)(2)例4.不通过求值,指出下列各式大于零还是小于零:(1);(2) 师:例1中体现出什么基础知识?例2(1)中体现什么基本方法?例2(2)中为什么与同时取得最大值?例2(3)通过观察题目结构可以利用什么方法转化成什么问题?例3 基本三角函数的最小正周期是什么?怎样利用换元法解决(1)(2)的周期?对一般的函数如何求出周期? 使学生巩固掌握正弦函数的性质。从特殊到一般,类比思维
归纳小结 1.知识:正弦函数的性质。2.思想方法:数形结合思想、换元法、类比法。 学生反思本节内容,对知识进行总结,教师对思想方法进行提炼。 让学生学会学习,学会总结。
布置作业 层次1:43页A中3、5;B中3。层次2:43页A中4。 层次1要求所有学生完成;层次2要求中等以上水平完成。 使学生进一步巩固和应用所学知识。
w.w.w.k.s.5.u.c.o.m
www.
图(2)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
