第5课时 教师版-函数的表示方法(2)
文档属性
| 名称 | 第5课时 教师版-函数的表示方法(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 86.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-17 00:00:00 | ||
图片预览

文档简介
第五课时 函数的表示方法(2)
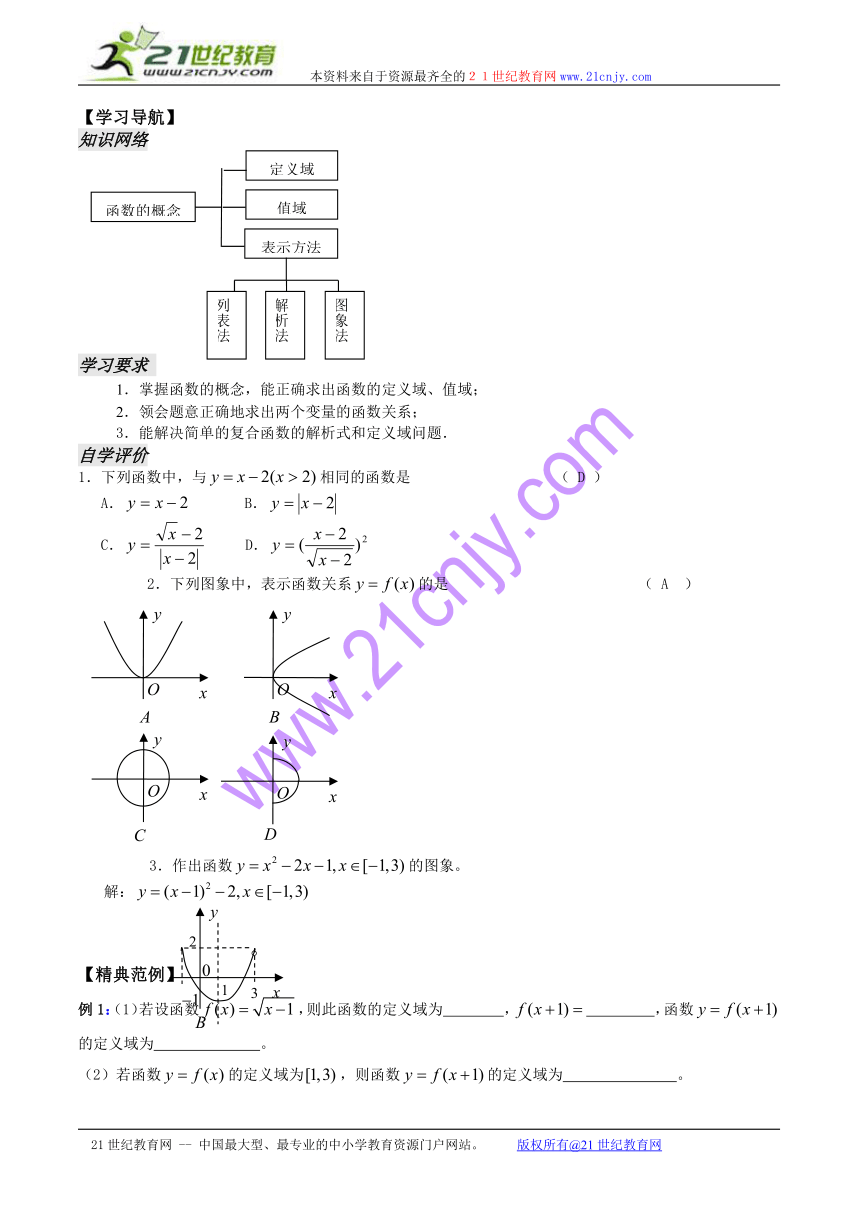
【学习导航】
知识网络
学习要求
1.掌握函数的概念,能正确求出函数的定义域、值域;
2.领会题意正确地求出两个变量的函数关系;
3.能解决简单的复合函数的解析式和定义域问题.
自学评价
1.下列函数中,与相同的函数是 ( D )
A. B.
C. D.
2.下列图象中,表示函数关系的是 ( A )
3.作出函数的图象。
解:
【精典范例】
例1:(1)若设函数,则此函数的定义域为 , ,函数的定义域为 。
(2)若函数的定义域为,则函数的定义域为 。
解:(1)由得,∴的定义域为,,
∴的定义域为。
(2)从(1)的解决可以体会,(1)中函数的定义域实际可以由求出。从形式上看,函数的定义域为,即“”后面的“( )”内的范围为,故的定义域应由得到,即。
例2:如图实线部分,某电影院的窗户的上部呈半圆形,下部呈矩形。已知窗户的外框的周长是,矩形的水平边的长是,求窗户的采光面的面积与的函数解析式,并指出函数的定义域。
【解】由题意,
,
,
∴,
即。
由问题的实际意义可知:
,解得。
所以,与的函数解析式是
,函数的定义域是
。
例3.若函数的定义域为,求实数的取值范围.
【解】由题意知,方程
① 无实数解,
(1)若,则方程①即,无实数解;
(2)若,则“方程①无实数解”等价于,
解得,
综上所述,实数的取值范围为
。
追踪训练一
1.函数的定义域为 ()
2.动点从边长为的正方形的顶点出发,顺次经过、、再回到,设表示点的行程,表示线段的长,求关于的函数解析式。
答案:
【选修延伸】
一、函数的值域
例4: 求函数的值域。
【分析】解析式的分子、分母都含变量,我们应设法减少变化的地方;
【解】,
∵, ∴,
即函数的值域为.
例5.求函数的值域。
【解】令 (),
则,
,
当时,,
∴函数的值域为.
思维点拨
例4中我们减少了的个数后就可以求出函数的值域,该方法我们称为分离常数法,容易知道:形如 的值域为;例5通过换元解决根号的问题我们称这种方法为换元法。
追踪训练二
1.函数的值域为( )
2.函数的值域是 。
学生质疑
教师释疑
定义域
值域
表示方法
函数的概念
列表法
解析法
图象法
3
1
2
【学习导航】
知识网络
学习要求
1.掌握函数的概念,能正确求出函数的定义域、值域;
2.领会题意正确地求出两个变量的函数关系;
3.能解决简单的复合函数的解析式和定义域问题.
自学评价
1.下列函数中,与相同的函数是 ( D )
A. B.
C. D.
2.下列图象中,表示函数关系的是 ( A )
3.作出函数的图象。
解:
【精典范例】
例1:(1)若设函数,则此函数的定义域为 , ,函数的定义域为 。
(2)若函数的定义域为,则函数的定义域为 。
解:(1)由得,∴的定义域为,,
∴的定义域为。
(2)从(1)的解决可以体会,(1)中函数的定义域实际可以由求出。从形式上看,函数的定义域为,即“”后面的“( )”内的范围为,故的定义域应由得到,即。
例2:如图实线部分,某电影院的窗户的上部呈半圆形,下部呈矩形。已知窗户的外框的周长是,矩形的水平边的长是,求窗户的采光面的面积与的函数解析式,并指出函数的定义域。
【解】由题意,
,
,
∴,
即。
由问题的实际意义可知:
,解得。
所以,与的函数解析式是
,函数的定义域是
。
例3.若函数的定义域为,求实数的取值范围.
【解】由题意知,方程
① 无实数解,
(1)若,则方程①即,无实数解;
(2)若,则“方程①无实数解”等价于,
解得,
综上所述,实数的取值范围为
。
追踪训练一
1.函数的定义域为 ()
2.动点从边长为的正方形的顶点出发,顺次经过、、再回到,设表示点的行程,表示线段的长,求关于的函数解析式。
答案:
【选修延伸】
一、函数的值域
例4: 求函数的值域。
【分析】解析式的分子、分母都含变量,我们应设法减少变化的地方;
【解】,
∵, ∴,
即函数的值域为.
例5.求函数的值域。
【解】令 (),
则,
,
当时,,
∴函数的值域为.
思维点拨
例4中我们减少了的个数后就可以求出函数的值域,该方法我们称为分离常数法,容易知道:形如 的值域为;例5通过换元解决根号的问题我们称这种方法为换元法。
追踪训练二
1.函数的值域为( )
2.函数的值域是 。
学生质疑
教师释疑
定义域
值域
表示方法
函数的概念
列表法
解析法
图象法
3
1
2
