第15课 教师版-分数指数幂
图片预览


文档简介
第十五课时 分数指数幂(2)
【学习导航】
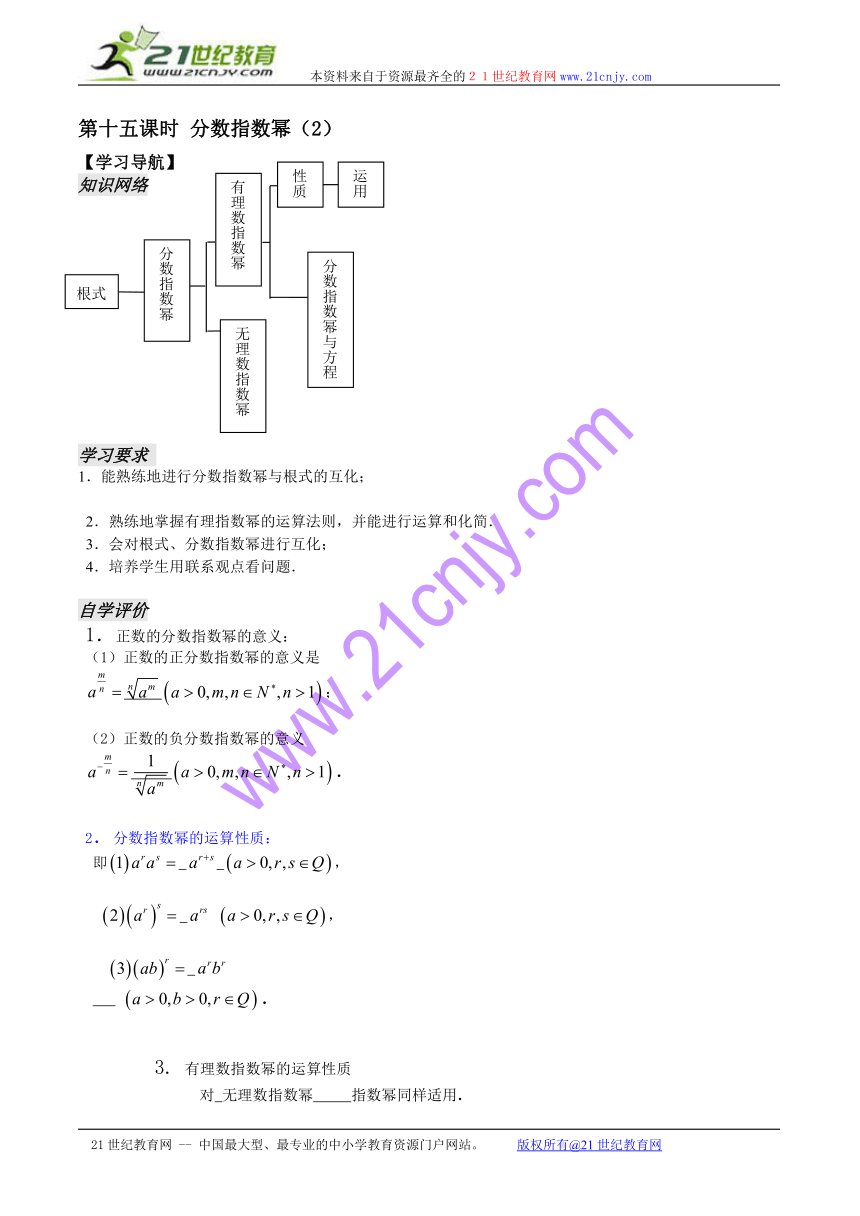
知识网络
学习要求
1.能熟练地进行分数指数幂与根式的互化;
2.熟练地掌握有理指数幂的运算法则,并能进行运算和化简.
3.会对根式、分数指数幂进行互化;
4.培养学生用联系观点看问题.
自学评价
1.正数的分数指数幂的意义:
(1)正数的正分数指数幂的意义是
;
(2)正数的负分数指数幂的意义
.
2.分数指数幂的运算性质:
即 ,
,
.
3. 有理数指数幂的运算性质
对 无理数指数幂 指数幂同样适用.
4. 的正分数指数幂等于 .
【精典范例】
例1:求值(1) ,(2)
(3), (4) .
【解】(1).
(2).
(3).
(4).
点评:解题的关键是利用分数指数幂的运算性质.
例2:用分数指数幂表示下列各式:
(1) ;(2) ;(3).
分析:先将根式写成分数指数幂的形式,然后进行运算.
【解】(1) .
(2).
(3).
点评:利用分数指数幂进行根式计算时,结果可化为根式的形式或保留分数指数幂的形式,但不能既有根式又有分数指数幂.
例3:已知a+a-1=3,求下列各式的值:
(1)-;(2)-
解:(1)因为(-)2=a1-2+a-1=3-2=1
所以-=±1
(2) -= (-)(a+1+a-1)= ±4
【解】
(1)∵
∴
∴.
(2)
=.
点评:要学会从整体上寻求已知条件与结论的联系;指数的概念推广后,初中所学的乘法公式和因式分解的变形技巧同样适用.
追踪训练一
1. 计算下列各式的值(式中字母都是正数).
(1)(xy2··)·
(2)·
解:(1)原式=····
(2)原式=[[]
=a1·a1=a2
2. 已知,求的值.
解:,
∴,又,
,
又,
∴原式.
3. 已知,求的值.
解:,
.
【选修延伸】
一、分数指数幂与方程
例4: 利用指数的运算法则,解下列方程:
(1)43x+2=256×81-x
(2)2x+2-6×2x-1-8=0
解:(1)因为43x+2=256×81-x
所以26x+4=28×23-3x
所以6x+4=11-3x
所以x=
(2)因为2x+2-6×2x-1-8=0
所以4×2x-3×2x-8=0
所以2x=8
所以x=3
分析:利用分数指数幂的性质将方程两边转化为同底的指数幂.
【解】(1)原方程可化为:,
,,∴
原方程的解为.
(2)原方程可化为:,
∴,,
原方程的解为.
点评:将指数方程转化为一元一次或一元二次方程是解题的关键.
思维点拔:
(1)根式与分数指数幂运算要灵活地互化;(2)一般地在化简过程中,先将根式化为分数指数幂,然后利用同底运算性质进行运算.
追踪训练二
1.化简:
解:
.
2.( )
3.设a>1,b>0,ab+a-b=2,则ab-a-b()
或
学生质疑
教师释疑
根式
分数指数幂
有理数指数幂
无理数指数幂
性质
运用
分数指数幂与方程
【学习导航】
知识网络
学习要求
1.能熟练地进行分数指数幂与根式的互化;
2.熟练地掌握有理指数幂的运算法则,并能进行运算和化简.
3.会对根式、分数指数幂进行互化;
4.培养学生用联系观点看问题.
自学评价
1.正数的分数指数幂的意义:
(1)正数的正分数指数幂的意义是
;
(2)正数的负分数指数幂的意义
.
2.分数指数幂的运算性质:
即 ,
,
.
3. 有理数指数幂的运算性质
对 无理数指数幂 指数幂同样适用.
4. 的正分数指数幂等于 .
【精典范例】
例1:求值(1) ,(2)
(3), (4) .
【解】(1).
(2).
(3).
(4).
点评:解题的关键是利用分数指数幂的运算性质.
例2:用分数指数幂表示下列各式:
(1) ;(2) ;(3).
分析:先将根式写成分数指数幂的形式,然后进行运算.
【解】(1) .
(2).
(3).
点评:利用分数指数幂进行根式计算时,结果可化为根式的形式或保留分数指数幂的形式,但不能既有根式又有分数指数幂.
例3:已知a+a-1=3,求下列各式的值:
(1)-;(2)-
解:(1)因为(-)2=a1-2+a-1=3-2=1
所以-=±1
(2) -= (-)(a+1+a-1)= ±4
【解】
(1)∵
∴
∴.
(2)
=.
点评:要学会从整体上寻求已知条件与结论的联系;指数的概念推广后,初中所学的乘法公式和因式分解的变形技巧同样适用.
追踪训练一
1. 计算下列各式的值(式中字母都是正数).
(1)(xy2··)·
(2)·
解:(1)原式=····
(2)原式=[[]
=a1·a1=a2
2. 已知,求的值.
解:,
∴,又,
,
又,
∴原式.
3. 已知,求的值.
解:,
.
【选修延伸】
一、分数指数幂与方程
例4: 利用指数的运算法则,解下列方程:
(1)43x+2=256×81-x
(2)2x+2-6×2x-1-8=0
解:(1)因为43x+2=256×81-x
所以26x+4=28×23-3x
所以6x+4=11-3x
所以x=
(2)因为2x+2-6×2x-1-8=0
所以4×2x-3×2x-8=0
所以2x=8
所以x=3
分析:利用分数指数幂的性质将方程两边转化为同底的指数幂.
【解】(1)原方程可化为:,
,,∴
原方程的解为.
(2)原方程可化为:,
∴,,
原方程的解为.
点评:将指数方程转化为一元一次或一元二次方程是解题的关键.
思维点拔:
(1)根式与分数指数幂运算要灵活地互化;(2)一般地在化简过程中,先将根式化为分数指数幂,然后利用同底运算性质进行运算.
追踪训练二
1.化简:
解:
.
2.( )
3.设a>1,b>0,ab+a-b=2,则ab-a-b()
或
学生质疑
教师释疑
根式
分数指数幂
有理数指数幂
无理数指数幂
性质
运用
分数指数幂与方程
