23.2中心对称(2010年中考演练同步作业)
文档属性
| 名称 | 23.2中心对称(2010年中考演练同步作业) |
|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-16 00:00:00 | ||
图片预览


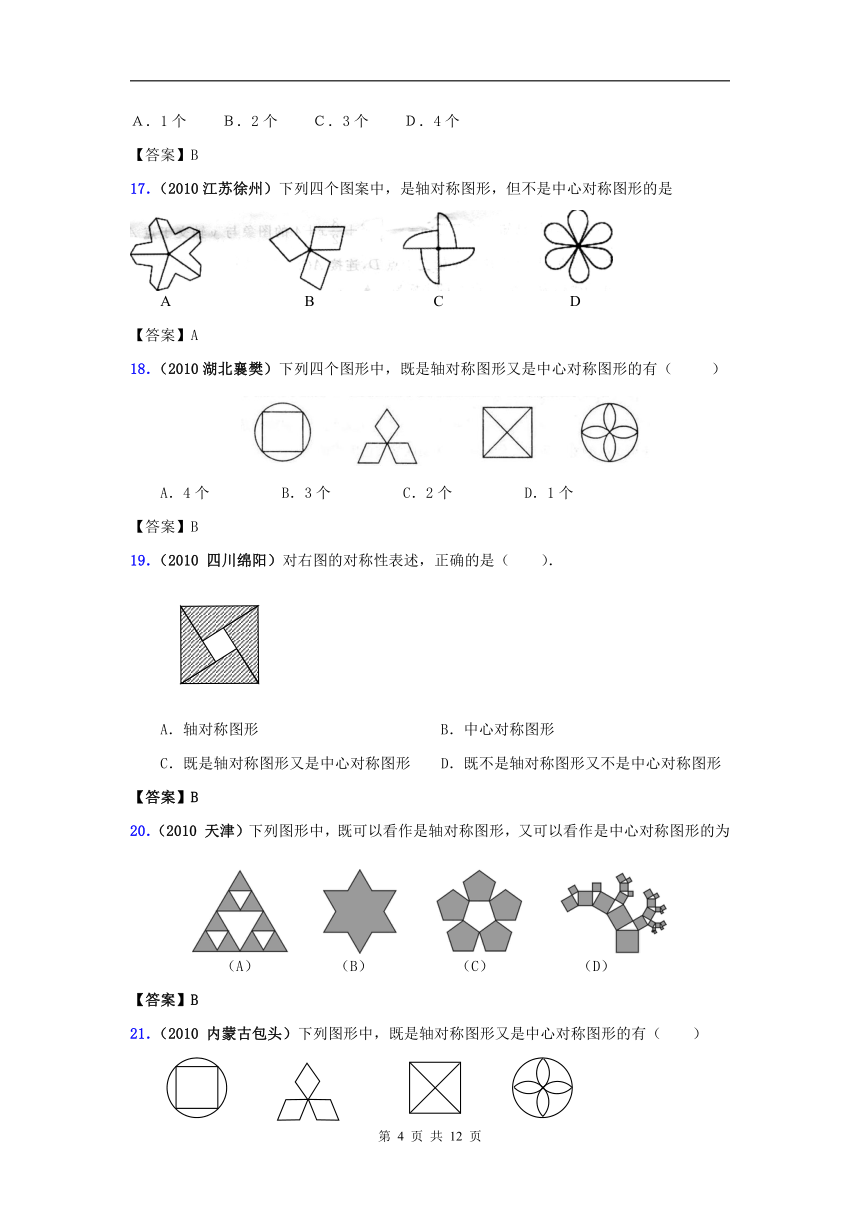
文档简介
23.2中心对称
一、选择题
1.(2010山东青岛)下列图形中,中心对称图形有( ).
【答案】C
2.(2010浙江宁波)下列各图是选自历届世博会会徽中的图案,其中是中心对称图形的是
【答案】C
3.(2010浙江湖州)如图,如果甲、乙关于点O成中心对称,则乙图中不符合题意的一块是( )
A. B. C. D.
【答案】C.
4.(2010湖南常德)下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
【答案】D
5.(2010江苏扬州)在等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】B
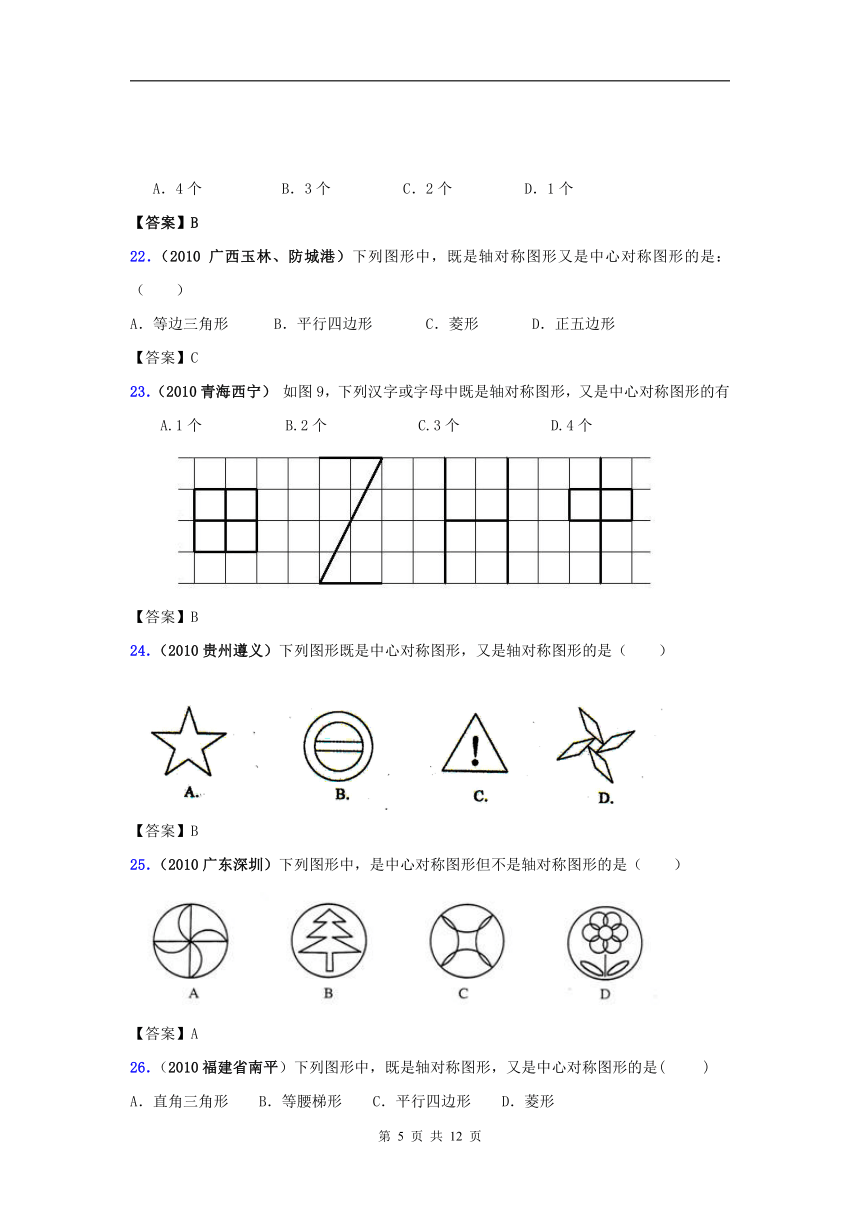
6.(2010黑龙江哈尔滨)一列图形中,是中心对称图形的是( )
【答案】D
7.(2010甘肃兰州)观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有
A.1个 B.2个 C.3个 D.4个
【答案】B
8.(2010江苏盐城)以下图形中,既是轴对称图形,又是中心对称图形的是
A.等边三角形 B.矩形 C.等腰梯形 D.平行四边形
【答案】B
9.(2010 浙江义乌)下列几何图形中,即是中心对称图形又是轴对称图形的是( )
A.正三角形 B.等腰直角三角形 C.等腰梯形 D.正方形
【答案】D
10.(2010 江苏连云港)下列四个多边形:①等边三角形;②正方形;③正五边形;④正六边形.其中,既是轴对称图形又是中心对称图形的是( )
A.①② B.②③ C.②④ D.①④
【答案】C
11.(2010江苏无锡)下列图形中,是中心对称图形但不是轴对称图形的是( )
【答案】B
12.(2010 山东省德州)下面的图形中,既是轴对称图形又是中心对称图形的是
(A) (B) (C) (D)
【答案】B
13.(2010 山东莱芜)在下列四个图案中既是轴对称图形,又是中心对称图形的是
A. B. C. D.
【答案】B
14.(2010福建宁德)下列四张扑克牌图案,属于中心对称的是( ).
【答案】B
15.(2010湖南怀化)下列图形中,是中心对称图形但不是轴对称图形的是( )
【答案】B
16.(2010山东泰安)下列图形:
其中,既是轴对称图形,又是中心对称图功的个数是( )
A.1个 B.2个 C.3个 D.4个
【答案】B
17.(2010江苏徐州)下列四个图案中,是轴对称图形,但不是中心对称图形的是
【答案】A
18.(2010湖北襄樊)下列四个图形中,既是轴对称图形又是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
【答案】B
19.(2010 四川绵阳)对右图的对称性表述,正确的是( ).
A.轴对称图形 B.中心对称图形
C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形又不是中心对称图形
【答案】B
20.(2010 天津)下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为
(A) (B) (C) (D)
【答案】B
21.(2010 内蒙古包头)下列图形中,既是轴对称图形又是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
【答案】B
22.(2010 广西玉林、防城港)下列图形中,既是轴对称图形又是中心对称图形的是: ( )
A.等边三角形 B.平行四边形 C.菱形 D.正五边形
【答案】C
23.(2010青海西宁) 如图9,下列汉字或字母中既是轴对称图形,又是中心对称图形的有
A.1个 B.2个 C.3个 D.4个
【答案】B
24.(2010贵州遵义)下列图形既是中心对称图形,又是轴对称图形的是( )
【答案】B
25.(2010广东深圳)下列图形中,是中心对称图形但不是轴对称图形的是( )
【答案】A
26.(2010福建省南平)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.直角三角形 B.等腰梯形 C.平行四边形 D.菱形
【答案】D
27.(2010 福建莆田)下列图形中,是中心对称图形的是( )
【答案】B
28.(2010广东湛江)下列交通标志既是中心对称图形,又是轴对称图形的是( )
【答案】D
29.(2010内蒙呼和浩特)在下列图形中,既是轴对称图形,又是中心对称图形的是 ( )
【答案】C
30.(2010内蒙赤峰)下列图形中既是轴对称图形,又是中心对称图形的是
( )
【答案】B
二、填空题
1.(2010江苏南京)如图,AB⊥BC,AB=BC=2cm,弧OA与弧OC关于点O中心对称,则AB、BC、弧CO、弧OA所围成的面积是 cm2。
【答案】2
2.(2010山东威海)如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为 .
【答案】﹙0,1﹚;
3.(2010 四川南充)如图,□ABCD中,点A关于点O的对称点是点____.
【答案】C
4.(2010浙江金华)如图, 在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 则对称中心E点的坐标是 .
【答案】(3,-1)
5.(2010广西河池)写出一个既有轴对称性质又有中心对称性质的图形名称: .
【答案】线段、圆、正方形、矩形、菱形、正边形(为正整数)等(写出其中一个即可)
6.(2010云南曲靖)在你认识的图形中,写出一个既是轴对称又是中心对称的图形名称: 。
【答案】圆答案不唯一
三、解答题
1.(2010四川内江)阅读理解:
我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为(,).
观察应用:
(1)如图,在平面直角坐标系中,若点P1(0,-1)、P2(2,3)的对称中心是点A,则点A的坐标为 ;
(2)另取两点B(-1.6,2.1)、C(-1,0).有一电子青蛙从点P1处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,….则P3、P8的坐标分别为 , ;
拓展延伸:
(3)求出点P2012的坐标,并直接写出在x轴上与点P2012、点C构成等腰三角形的点的坐标.
【答案】解:设A、P3、P4、…、Pn点的坐标依次为(x,y)、(x3,y3)、(x4,y4)、…、(xn,yn)(n≥3,且为正整数).
(1)P1(0,-1)、P2(2,3),
∴x==1,y==1,
∴A(1,1).
(2)∵点P3与P2关于点B成中心对称,且B(-1.6,2.1),
∴=-1.6,=2.1,
解得x3=-5.2,y3=1.2,
∴P3(-5.2,1.2).
∵点P4与P3关于点C成中心对称,且C(-1,0),
∴=-1,=0,
解得x4=3.2,y4=-1.2,
∴P4(3.2,-1.2) .
同理可得P5(-1.2,3.2)→P6(-2,1)→P7(0,-1)→P8 (2, 3).
(3)∵P1(0,-1)→P2(2,3)→P3(-5.2,1.2).→P4(3.2,-1.2)→P5(-1.2,3.2)→P6(-2,1)→P7(0,-1)→P8 (2, 3) …
∴P7的坐标和P1的坐标相同,P8的坐标和P2的坐标相同,即坐标以6为周期循环,
∵2012÷6=335……2,
∴P2012的坐标与P2的坐标相同,为P2012 (2,3);
在x轴上与点P2012、点C构成等腰三角形的点的坐标为
(-3-1,0),(2,0),(3-1,0),(5,0).
2.(2010浙江绍兴)分别按下列要求解答:
(1)在图1中,将△ABC先向左平移5个单位,再作关于直线AB的轴对称图形,经两次变换后得到△A1B1 C1.画出△A1B1C1;
(2)在图2中,△ABC经变换得到△A2B2C2.描述变换过程.
【答案】
(1) 如图.
(2) 将△ABC先关于点A作中心对称图形,再向左平移
2个单位,得到△A2B2C2.(变换过程不唯一)
3.(2010 甘肃)(6分)图①、图②均为的正方形网格,点在格点(小正方形的顶点)上.
(1)在图①中确定格点,并画出一个以为顶点的四边形,使其为轴对称图形;
(2)在图②中确定格点,并画出一个以为顶点的四边形,使其为中心对称图形.
【答案】解:(1)有以下答案供参考:
(2)有以下答案供参考:
4.(2010新疆维吾尔自治区新疆建设兵团)用四块如下图(1)所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形)
【答案】解法不唯一。
例解:
A
C
D
C
B
A
D
B
A
图②
C
B
A
图①
C
B
A
C
B
A
12
11
10
9
8
7
6
5
4
3
2
1
11
0 1 2 3 4 5 6 7 8 9 10 12
C2
B2
A2
C
B
A
12
11
10
9
8
7
6
5
4
3
2
1
11
0 1 2 3 4 5 6 7 8 9 10 12
P1
B
P2
C
O
y
x
5
B1
C1
A1
C
B
-4
4
3
2
1
-1
-3
-2
-1
2
1
y
x
O
A
(第14题图)
O
B
C
D
(第12题)
A
A
B
C
D
A. B. C. D.
A. B. C. D.
图4
A B C D
!
(D)
(A)
(B)
(C)
B
C
E
A
B
C
E
第 3 页 共 12 页
一、选择题
1.(2010山东青岛)下列图形中,中心对称图形有( ).
【答案】C
2.(2010浙江宁波)下列各图是选自历届世博会会徽中的图案,其中是中心对称图形的是
【答案】C
3.(2010浙江湖州)如图,如果甲、乙关于点O成中心对称,则乙图中不符合题意的一块是( )
A. B. C. D.
【答案】C.
4.(2010湖南常德)下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
【答案】D
5.(2010江苏扬州)在等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】B
6.(2010黑龙江哈尔滨)一列图形中,是中心对称图形的是( )
【答案】D
7.(2010甘肃兰州)观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有
A.1个 B.2个 C.3个 D.4个
【答案】B
8.(2010江苏盐城)以下图形中,既是轴对称图形,又是中心对称图形的是
A.等边三角形 B.矩形 C.等腰梯形 D.平行四边形
【答案】B
9.(2010 浙江义乌)下列几何图形中,即是中心对称图形又是轴对称图形的是( )
A.正三角形 B.等腰直角三角形 C.等腰梯形 D.正方形
【答案】D
10.(2010 江苏连云港)下列四个多边形:①等边三角形;②正方形;③正五边形;④正六边形.其中,既是轴对称图形又是中心对称图形的是( )
A.①② B.②③ C.②④ D.①④
【答案】C
11.(2010江苏无锡)下列图形中,是中心对称图形但不是轴对称图形的是( )
【答案】B
12.(2010 山东省德州)下面的图形中,既是轴对称图形又是中心对称图形的是
(A) (B) (C) (D)
【答案】B
13.(2010 山东莱芜)在下列四个图案中既是轴对称图形,又是中心对称图形的是
A. B. C. D.
【答案】B
14.(2010福建宁德)下列四张扑克牌图案,属于中心对称的是( ).
【答案】B
15.(2010湖南怀化)下列图形中,是中心对称图形但不是轴对称图形的是( )
【答案】B
16.(2010山东泰安)下列图形:
其中,既是轴对称图形,又是中心对称图功的个数是( )
A.1个 B.2个 C.3个 D.4个
【答案】B
17.(2010江苏徐州)下列四个图案中,是轴对称图形,但不是中心对称图形的是
【答案】A
18.(2010湖北襄樊)下列四个图形中,既是轴对称图形又是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
【答案】B
19.(2010 四川绵阳)对右图的对称性表述,正确的是( ).
A.轴对称图形 B.中心对称图形
C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形又不是中心对称图形
【答案】B
20.(2010 天津)下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为
(A) (B) (C) (D)
【答案】B
21.(2010 内蒙古包头)下列图形中,既是轴对称图形又是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
【答案】B
22.(2010 广西玉林、防城港)下列图形中,既是轴对称图形又是中心对称图形的是: ( )
A.等边三角形 B.平行四边形 C.菱形 D.正五边形
【答案】C
23.(2010青海西宁) 如图9,下列汉字或字母中既是轴对称图形,又是中心对称图形的有
A.1个 B.2个 C.3个 D.4个
【答案】B
24.(2010贵州遵义)下列图形既是中心对称图形,又是轴对称图形的是( )
【答案】B
25.(2010广东深圳)下列图形中,是中心对称图形但不是轴对称图形的是( )
【答案】A
26.(2010福建省南平)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.直角三角形 B.等腰梯形 C.平行四边形 D.菱形
【答案】D
27.(2010 福建莆田)下列图形中,是中心对称图形的是( )
【答案】B
28.(2010广东湛江)下列交通标志既是中心对称图形,又是轴对称图形的是( )
【答案】D
29.(2010内蒙呼和浩特)在下列图形中,既是轴对称图形,又是中心对称图形的是 ( )
【答案】C
30.(2010内蒙赤峰)下列图形中既是轴对称图形,又是中心对称图形的是
( )
【答案】B
二、填空题
1.(2010江苏南京)如图,AB⊥BC,AB=BC=2cm,弧OA与弧OC关于点O中心对称,则AB、BC、弧CO、弧OA所围成的面积是 cm2。
【答案】2
2.(2010山东威海)如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为 .
【答案】﹙0,1﹚;
3.(2010 四川南充)如图,□ABCD中,点A关于点O的对称点是点____.
【答案】C
4.(2010浙江金华)如图, 在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 则对称中心E点的坐标是 .
【答案】(3,-1)
5.(2010广西河池)写出一个既有轴对称性质又有中心对称性质的图形名称: .
【答案】线段、圆、正方形、矩形、菱形、正边形(为正整数)等(写出其中一个即可)
6.(2010云南曲靖)在你认识的图形中,写出一个既是轴对称又是中心对称的图形名称: 。
【答案】圆答案不唯一
三、解答题
1.(2010四川内江)阅读理解:
我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为(,).
观察应用:
(1)如图,在平面直角坐标系中,若点P1(0,-1)、P2(2,3)的对称中心是点A,则点A的坐标为 ;
(2)另取两点B(-1.6,2.1)、C(-1,0).有一电子青蛙从点P1处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,….则P3、P8的坐标分别为 , ;
拓展延伸:
(3)求出点P2012的坐标,并直接写出在x轴上与点P2012、点C构成等腰三角形的点的坐标.
【答案】解:设A、P3、P4、…、Pn点的坐标依次为(x,y)、(x3,y3)、(x4,y4)、…、(xn,yn)(n≥3,且为正整数).
(1)P1(0,-1)、P2(2,3),
∴x==1,y==1,
∴A(1,1).
(2)∵点P3与P2关于点B成中心对称,且B(-1.6,2.1),
∴=-1.6,=2.1,
解得x3=-5.2,y3=1.2,
∴P3(-5.2,1.2).
∵点P4与P3关于点C成中心对称,且C(-1,0),
∴=-1,=0,
解得x4=3.2,y4=-1.2,
∴P4(3.2,-1.2) .
同理可得P5(-1.2,3.2)→P6(-2,1)→P7(0,-1)→P8 (2, 3).
(3)∵P1(0,-1)→P2(2,3)→P3(-5.2,1.2).→P4(3.2,-1.2)→P5(-1.2,3.2)→P6(-2,1)→P7(0,-1)→P8 (2, 3) …
∴P7的坐标和P1的坐标相同,P8的坐标和P2的坐标相同,即坐标以6为周期循环,
∵2012÷6=335……2,
∴P2012的坐标与P2的坐标相同,为P2012 (2,3);
在x轴上与点P2012、点C构成等腰三角形的点的坐标为
(-3-1,0),(2,0),(3-1,0),(5,0).
2.(2010浙江绍兴)分别按下列要求解答:
(1)在图1中,将△ABC先向左平移5个单位,再作关于直线AB的轴对称图形,经两次变换后得到△A1B1 C1.画出△A1B1C1;
(2)在图2中,△ABC经变换得到△A2B2C2.描述变换过程.
【答案】
(1) 如图.
(2) 将△ABC先关于点A作中心对称图形,再向左平移
2个单位,得到△A2B2C2.(变换过程不唯一)
3.(2010 甘肃)(6分)图①、图②均为的正方形网格,点在格点(小正方形的顶点)上.
(1)在图①中确定格点,并画出一个以为顶点的四边形,使其为轴对称图形;
(2)在图②中确定格点,并画出一个以为顶点的四边形,使其为中心对称图形.
【答案】解:(1)有以下答案供参考:
(2)有以下答案供参考:
4.(2010新疆维吾尔自治区新疆建设兵团)用四块如下图(1)所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形)
【答案】解法不唯一。
例解:
A
C
D
C
B
A
D
B
A
图②
C
B
A
图①
C
B
A
C
B
A
12
11
10
9
8
7
6
5
4
3
2
1
11
0 1 2 3 4 5 6 7 8 9 10 12
C2
B2
A2
C
B
A
12
11
10
9
8
7
6
5
4
3
2
1
11
0 1 2 3 4 5 6 7 8 9 10 12
P1
B
P2
C
O
y
x
5
B1
C1
A1
C
B
-4
4
3
2
1
-1
-3
-2
-1
2
1
y
x
O
A
(第14题图)
O
B
C
D
(第12题)
A
A
B
C
D
A. B. C. D.
A. B. C. D.
图4
A B C D
!
(D)
(A)
(B)
(C)
B
C
E
A
B
C
E
第 3 页 共 12 页
同课章节目录
