24.2.1点与圆有关的位置关系(2010年中考演练同步作业)
文档属性
| 名称 | 24.2.1点与圆有关的位置关系(2010年中考演练同步作业) |  | |
| 格式 | rar | ||
| 文件大小 | 508.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-16 21:12:00 | ||
图片预览


文档简介
24.1点与圆有关的位置关系
一、选择题
1.(2010甘肃兰州) 有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有
A.4个 B.3个 C. 2个 D. 1个
【答案】B
2.(2010江苏南通) 如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是
A.1 B.
C. D.2
【答案】D
3.(2010台湾)如图(二),为圆O的直径,C、D两点均在圆上,其中与交于
E点,且。若=4,=2,则长度为何?
(A) 6 (B) 7 (C) 8 (D) 9 。
【答案】C
4.(2010浙江嘉兴)如图,A、B、C是⊙O上的三点,已知,则( )
(A) (B)
(C) (D)
【答案】C
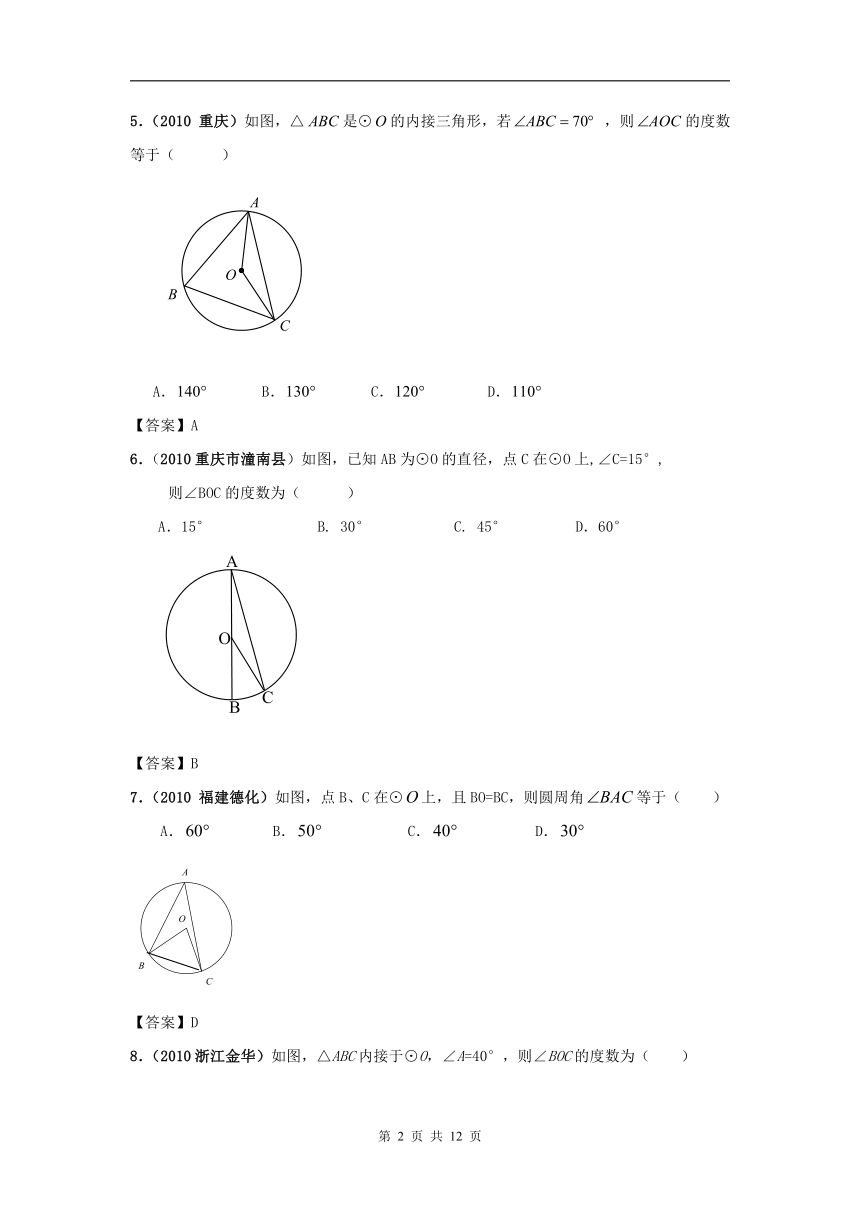
5.(2010 重庆)如图,△是⊙的内接三角形,若 ,则的度数等于( )
A. B. C. D.
【答案】A
6.(2010重庆市潼南县)如图,已知AB为⊙O的直径,点C在⊙O上,∠C=15°,
则∠BOC的度数为( )
A.15° B. 30° C. 45° D.60°
【答案】B
7.(2010 福建德化)如图,点B、C在⊙上,且BO=BC,则圆周角等于( )
A. B. C. D.
【答案】D
8.(2010浙江金华)如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为( )
A. 20° B. 40° C. 60° D. 80°
【答案】D
9.(2010四川宜宾)若⊙O的半径为4cm,点A到圆心O的距离为3cm,那么点A与⊙O的位置关系是( )
A.点A在圆内 B.点A在圆上 c.点A在圆外 D.不能确定
【答案】A
10.(2010湖北荆门)如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为
A.2 B. C.1 D.2
【答案】B
11.(2010湖北荆州)△ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.如图,若 弧A B 的长为12cm,那么弧AC 的长是
A.10cm B.9cm C.8cm D.6cm
【答案】C
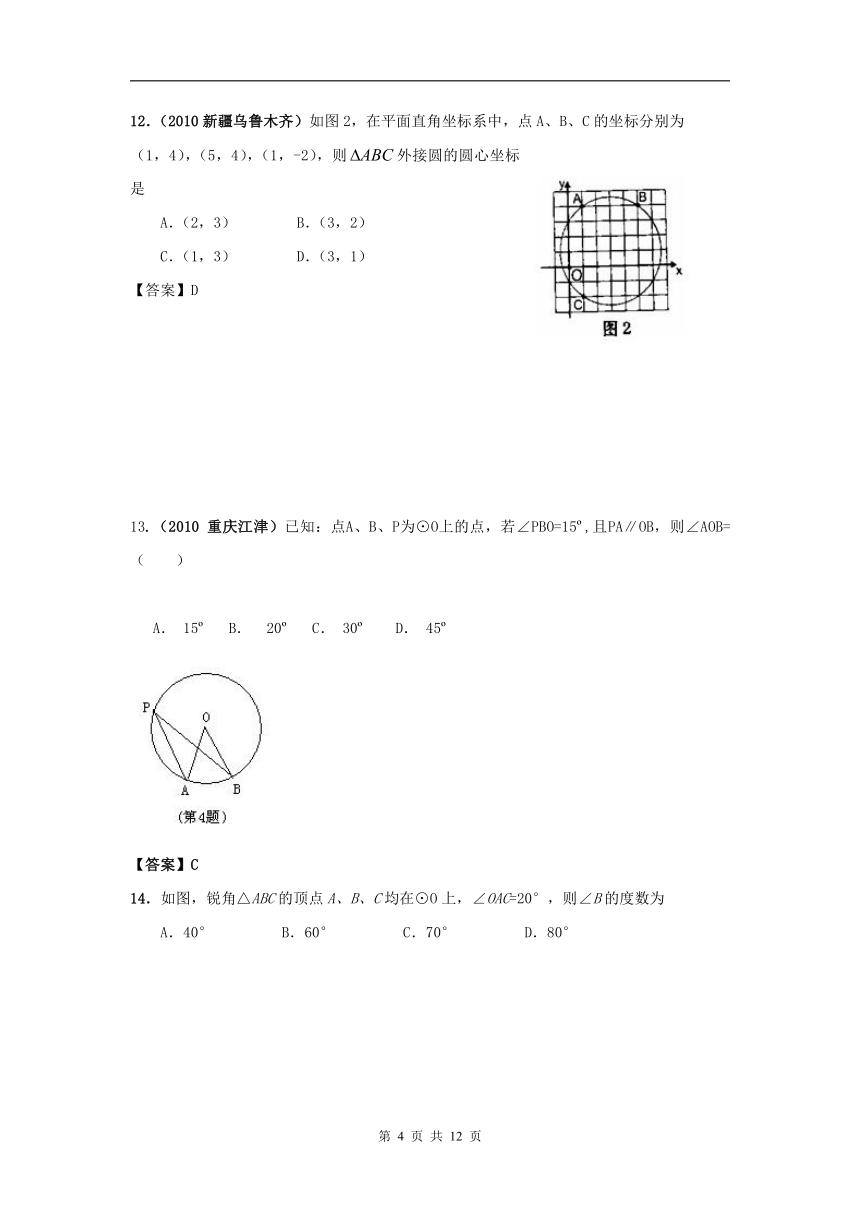
12.(2010新疆乌鲁木齐)如图2,在平面直角坐标系中,点A、B、C的坐标分别为
(1,4),(5,4),(1,-2),则外接圆的圆心坐标是
A.(2,3) B.(3,2)
C.(1,3) D.(3,1)
【答案】D
13.(2010 重庆江津)已知:点A、B、P为⊙O上的点,若∠PBO=15 ,且PA∥OB,则∠AOB=( )
A. 15 B. 20 C. 30 D. 45
【答案】C
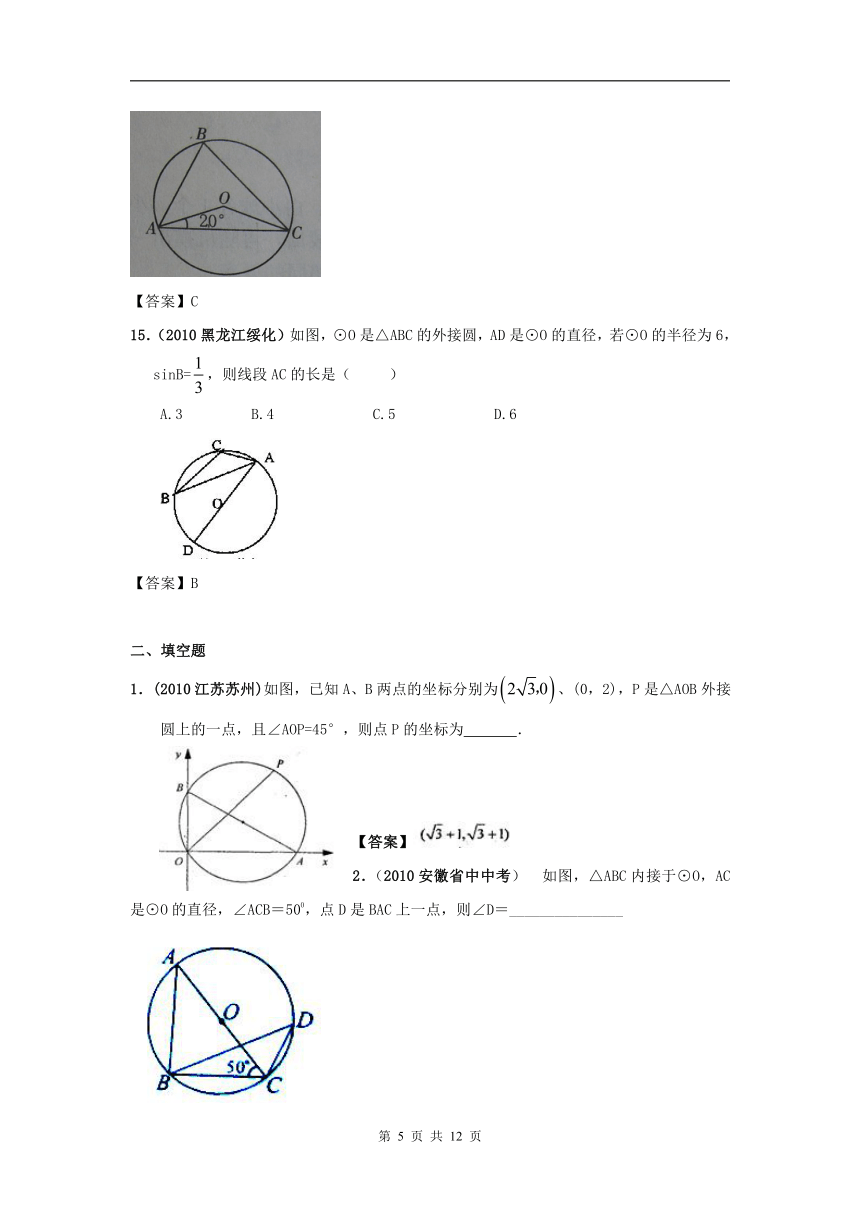
14.如图,锐角△ABC的顶点A、B、C均在⊙O上,∠OAC=20°,则∠B的度数为
A.40° B.60° C.70° D.80°
【答案】C
15.(2010黑龙江绥化)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为6,sinB=,则线段AC的长是( )
A.3 B.4 C.5 D.6
【答案】B
二、填空题
1.(2010江苏苏州)如图,已知A、B两点的坐标分别为、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 .
【答案】
2.(2010安徽省中中考) 如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=500,点D是BAC上一点,则∠D=_______________
【答案】
3.(2010山东青岛)如图,点A、B、C在⊙O上,若∠BAC = 24°,则∠BOC = °.
【答案】48
4.(2010山东威海)如图,AB为⊙O的直径,点C,D在⊙O上.若∠AOD=30°,则∠BCD的度数是 .
【答案】105°
5.(2010重庆綦江县)如图所示,A、B、C、D是圆上的点,∠1=68°,∠A=40°.则∠D=_______.
【答案】28°
6.(2010浙江绍兴)如图,⊙O是正三角形的外接圆,点在劣弧上,=22°,则的度数为_____________.
【答案】38°
7.(2010 浙江衢州) 如图,△ABC是⊙O的内接三角形,点D是的中点,
已知∠AOB=98°,∠COB=120°.则∠ABD的度数是 .
【答案】101°
8.(2010 江苏连云港)如图,点A、B、C在⊙O上,AB∥CD,∠B=22°,则∠A=________°.
【答案】44
9.(2010 四川成都)如图,内接于⊙O,,是⊙O上与点关于圆心成中心对称的点,是边上一点,连结.已知,,是线段上一动点,连结并延长交四边形的一边于点,且满足,则的值为_______________.
【答案】1和
10.(2010福建南平)如图,△ABC是⊙O的内接等边三角形,则∠BOC=_______°.
答案:120
三、解答题
1.(2010山东济宁)如图,为外接圆的直径,,垂足为点,的平分线交于点,连接,.
(1) 求证:;
(2) 请判断,,三点是否在以为圆心,以为半径的圆上?并说明理由.
【答案】
(1)证明:∵为直径,,
∴.∴.
(2)答:,,三点在以为圆心,以为半径的圆上.
理由:由(1)知:,∴.
∵,,,
∴.∴.
由(1)知:.∴.
∴,,三点在以为圆心,以为半径的圆上.
2.(2010 四川南充)如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC, OE=BC.
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
【答案】(1)解:连结OB和OC.
∵ OE⊥BC,∴ BE=CE.
∵ OE=BC,∴ ∠BOC=90°,∴ ∠BAC=45°.
(2)证明:∵ AD⊥BC,∴ ∠ADB=∠ADC=90°.
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD,
∴ ∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°.
∴ ∠GAF=∠BAG+∠CAF+∠BAC=90°.
∴ 四边形AFHG是正方形.
(3)解:由(2)得,∠BHC=90°,GH=HF=AD,GB=BD=6,CF=CD=4.
设AD的长为x,则 BH=GH-GB=x-6,CH=HF-CF=x-4.
在Rt△BCH中,BH2+CH2=BC2,∴ (x-6)2+(x-4)2=102.
解得,x1=12,x2=-2(不合题意,舍去).
∴ AD=12.
3.(2010 四川成都)已知:如图,内接于⊙O,为直径,弦于,是AD的中点,连结并延长交的延长线于点,连结,分别交、于点、.
(1)求证:是的外心;
(2)若,求的长;
(3)求证:.
【答案】(1)证明:∵C是AD的中点,∴AC=CD,
∴∠CAD=∠ABC
∵AB是⊙O的直径,∴∠ACB=90°。
∴∠CAD+∠AQC=90°
又CE⊥AB,∴∠ABC+∠PCQ=90°
∴∠AQC=∠PCQ
∴在△PCQ中,PC=PQ,
∵CE⊥直径AB,∴AC=AE
∴AE=CD
∴∠CAD=∠ACE。
∴在△APC中,有PA=PC,
∴PA=PC=PQ
∴P是△ACQ的外心。
(2)解:∵CE⊥直径AB于F,
∴在Rt△BCF中,由tan∠ABC=,CF=8,
得。
∴由勾股定理,得
∵AB是⊙O的直径,
∴在Rt△ACB中,由tan∠ABC=,
得。
易知Rt△ACB∽Rt△QCA,∴
∴。
(3)证明:∵AB是⊙O的直径,∴∠ACB=90°
∴∠DAB+∠ABD=90°
又CF⊥AB,∴∠ABG+∠G=90°
∴∠DAB=∠G;
∴Rt△AFP∽Rt△GFB,
∴,即
易知Rt△ACF∽Rt△CBF,
∴
∴
由(1),知PC=PQ,∴FP+PQ=FP+PC=FC
∴。
G
E
D
C
F
A
O
B
H
G
E
D
C
F
A
·
O
C
B
A
第10题
CFEBAD
·
O
BAD
AD
O
D
C
B
A
C
O
D
B
A
﹙第4题图﹚
·
C
B
A
O
O
B
C
A
B
C
O
A
(第4题)
图(二)
O
E
D
C
B
A
H
B
O
A
F
C
D
E
G
H
B
O
⌒
⌒
⌒
⌒
⌒
第 1 页 共 12 页
一、选择题
1.(2010甘肃兰州) 有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有
A.4个 B.3个 C. 2个 D. 1个
【答案】B
2.(2010江苏南通) 如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是
A.1 B.
C. D.2
【答案】D
3.(2010台湾)如图(二),为圆O的直径,C、D两点均在圆上,其中与交于
E点,且。若=4,=2,则长度为何?
(A) 6 (B) 7 (C) 8 (D) 9 。
【答案】C
4.(2010浙江嘉兴)如图,A、B、C是⊙O上的三点,已知,则( )
(A) (B)
(C) (D)
【答案】C
5.(2010 重庆)如图,△是⊙的内接三角形,若 ,则的度数等于( )
A. B. C. D.
【答案】A
6.(2010重庆市潼南县)如图,已知AB为⊙O的直径,点C在⊙O上,∠C=15°,
则∠BOC的度数为( )
A.15° B. 30° C. 45° D.60°
【答案】B
7.(2010 福建德化)如图,点B、C在⊙上,且BO=BC,则圆周角等于( )
A. B. C. D.
【答案】D
8.(2010浙江金华)如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为( )
A. 20° B. 40° C. 60° D. 80°
【答案】D
9.(2010四川宜宾)若⊙O的半径为4cm,点A到圆心O的距离为3cm,那么点A与⊙O的位置关系是( )
A.点A在圆内 B.点A在圆上 c.点A在圆外 D.不能确定
【答案】A
10.(2010湖北荆门)如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为
A.2 B. C.1 D.2
【答案】B
11.(2010湖北荆州)△ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.如图,若 弧A B 的长为12cm,那么弧AC 的长是
A.10cm B.9cm C.8cm D.6cm
【答案】C
12.(2010新疆乌鲁木齐)如图2,在平面直角坐标系中,点A、B、C的坐标分别为
(1,4),(5,4),(1,-2),则外接圆的圆心坐标是
A.(2,3) B.(3,2)
C.(1,3) D.(3,1)
【答案】D
13.(2010 重庆江津)已知:点A、B、P为⊙O上的点,若∠PBO=15 ,且PA∥OB,则∠AOB=( )
A. 15 B. 20 C. 30 D. 45
【答案】C
14.如图,锐角△ABC的顶点A、B、C均在⊙O上,∠OAC=20°,则∠B的度数为
A.40° B.60° C.70° D.80°
【答案】C
15.(2010黑龙江绥化)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为6,sinB=,则线段AC的长是( )
A.3 B.4 C.5 D.6
【答案】B
二、填空题
1.(2010江苏苏州)如图,已知A、B两点的坐标分别为、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 .
【答案】
2.(2010安徽省中中考) 如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=500,点D是BAC上一点,则∠D=_______________
【答案】
3.(2010山东青岛)如图,点A、B、C在⊙O上,若∠BAC = 24°,则∠BOC = °.
【答案】48
4.(2010山东威海)如图,AB为⊙O的直径,点C,D在⊙O上.若∠AOD=30°,则∠BCD的度数是 .
【答案】105°
5.(2010重庆綦江县)如图所示,A、B、C、D是圆上的点,∠1=68°,∠A=40°.则∠D=_______.
【答案】28°
6.(2010浙江绍兴)如图,⊙O是正三角形的外接圆,点在劣弧上,=22°,则的度数为_____________.
【答案】38°
7.(2010 浙江衢州) 如图,△ABC是⊙O的内接三角形,点D是的中点,
已知∠AOB=98°,∠COB=120°.则∠ABD的度数是 .
【答案】101°
8.(2010 江苏连云港)如图,点A、B、C在⊙O上,AB∥CD,∠B=22°,则∠A=________°.
【答案】44
9.(2010 四川成都)如图,内接于⊙O,,是⊙O上与点关于圆心成中心对称的点,是边上一点,连结.已知,,是线段上一动点,连结并延长交四边形的一边于点,且满足,则的值为_______________.
【答案】1和
10.(2010福建南平)如图,△ABC是⊙O的内接等边三角形,则∠BOC=_______°.
答案:120
三、解答题
1.(2010山东济宁)如图,为外接圆的直径,,垂足为点,的平分线交于点,连接,.
(1) 求证:;
(2) 请判断,,三点是否在以为圆心,以为半径的圆上?并说明理由.
【答案】
(1)证明:∵为直径,,
∴.∴.
(2)答:,,三点在以为圆心,以为半径的圆上.
理由:由(1)知:,∴.
∵,,,
∴.∴.
由(1)知:.∴.
∴,,三点在以为圆心,以为半径的圆上.
2.(2010 四川南充)如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC, OE=BC.
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
【答案】(1)解:连结OB和OC.
∵ OE⊥BC,∴ BE=CE.
∵ OE=BC,∴ ∠BOC=90°,∴ ∠BAC=45°.
(2)证明:∵ AD⊥BC,∴ ∠ADB=∠ADC=90°.
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD,
∴ ∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°.
∴ ∠GAF=∠BAG+∠CAF+∠BAC=90°.
∴ 四边形AFHG是正方形.
(3)解:由(2)得,∠BHC=90°,GH=HF=AD,GB=BD=6,CF=CD=4.
设AD的长为x,则 BH=GH-GB=x-6,CH=HF-CF=x-4.
在Rt△BCH中,BH2+CH2=BC2,∴ (x-6)2+(x-4)2=102.
解得,x1=12,x2=-2(不合题意,舍去).
∴ AD=12.
3.(2010 四川成都)已知:如图,内接于⊙O,为直径,弦于,是AD的中点,连结并延长交的延长线于点,连结,分别交、于点、.
(1)求证:是的外心;
(2)若,求的长;
(3)求证:.
【答案】(1)证明:∵C是AD的中点,∴AC=CD,
∴∠CAD=∠ABC
∵AB是⊙O的直径,∴∠ACB=90°。
∴∠CAD+∠AQC=90°
又CE⊥AB,∴∠ABC+∠PCQ=90°
∴∠AQC=∠PCQ
∴在△PCQ中,PC=PQ,
∵CE⊥直径AB,∴AC=AE
∴AE=CD
∴∠CAD=∠ACE。
∴在△APC中,有PA=PC,
∴PA=PC=PQ
∴P是△ACQ的外心。
(2)解:∵CE⊥直径AB于F,
∴在Rt△BCF中,由tan∠ABC=,CF=8,
得。
∴由勾股定理,得
∵AB是⊙O的直径,
∴在Rt△ACB中,由tan∠ABC=,
得。
易知Rt△ACB∽Rt△QCA,∴
∴。
(3)证明:∵AB是⊙O的直径,∴∠ACB=90°
∴∠DAB+∠ABD=90°
又CF⊥AB,∴∠ABG+∠G=90°
∴∠DAB=∠G;
∴Rt△AFP∽Rt△GFB,
∴,即
易知Rt△ACF∽Rt△CBF,
∴
∴
由(1),知PC=PQ,∴FP+PQ=FP+PC=FC
∴。
G
E
D
C
F
A
O
B
H
G
E
D
C
F
A
·
O
C
B
A
第10题
CFEBAD
·
O
BAD
AD
O
D
C
B
A
C
O
D
B
A
﹙第4题图﹚
·
C
B
A
O
O
B
C
A
B
C
O
A
(第4题)
图(二)
O
E
D
C
B
A
H
B
O
A
F
C
D
E
G
H
B
O
⌒
⌒
⌒
⌒
⌒
第 1 页 共 12 页
同课章节目录
