24.2.2直线与圆的位置关系2(2010年中考演练同步作业)
文档属性
| 名称 | 24.2.2直线与圆的位置关系2(2010年中考演练同步作业) |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-16 21:06:00 | ||
图片预览




文档简介
24.2.2直线与圆的位置关系
解答题
1.(2010 广东汕头)如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.
(1)求∠POA的度数;
(2)计算弦AB的长.
【答案】解:(1)∵PA与⊙O相切于A点
∴OA⊥AP
在Rt△OAP中,由OA=2,OP=4得
∴
∴.
(2)∵弦AB⊥OP,
∴,
∵
∴
∴
∴.
2.(2010 天津)已知是⊙的直径,是⊙的切线,是切点,与⊙交于点.
(Ⅰ)如图①,若,,求的长(结果保留根号);
(Ⅱ)如图②,若为的中点,求证直线是⊙的切线.
【答案】解:(Ⅰ)∵ 是⊙的直径,是切线,
∴ .
在Rt△中,,,
∴ .
由勾股定理,得. ..................5分
(Ⅱ)如图,连接、,
∵ 是⊙的直径,
∴ ,有.
在Rt△中,为的中点,
∴ .
∴ .
又 ∵,
∴.
∵ ,
∴ .
即 .
∴ 直线是⊙的切线.
3.(2010 内蒙古包头)如图,已知是的直径,点在上,过点的直线与的延长线交于点,,.
(1)求证:是的切线;
(2)求证:;
(3)点是的中点,交于点,若,求的值.
【答案】解:(1),
又,
.
又是的直径,
,
,即,
而是的半径,
是的切线.
(2),
,
又,
.
(3)连接,
点是的中点,,,
而,,而,
,,,
又是的直径,,
.
,.
4.(2010广西桂林)如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,
FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.[]
【答案】证明(1)连结OF
∵FH是⊙O的切线
∴OF⊥FH
∵FH∥BC ,
∴OF垂直平分BC
∴
∴AF平分∠BAC
(2)证明:由(1)及题设条件可知
∠1=∠2,∠4=∠3,∠5=∠2
∴∠1+∠4=∠2+∠3
∴∠1+∠4=∠5+∠3
∠FDB=∠FBD
∴BF=FD
(3)解: 在△BFE和△AFB中
∵∠5=∠2=∠1,∠F=∠F
∴△BFE∽△AFB
∴,
∴
∴
∴
∴AD==
5.(2010 广西玉林、防城港)(8分)如图8,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45,过点C的直线与⊙O、MN分别交于A、D两点,过C作CE⊥BD于点E。
(1)求证:CE是⊙O的切线;
(2)若∠D=30,BD=2+2,求⊙O的半径r。
【答案】(1)证明:连接OB,OC,MN是⊙O的切线,所以OB⊥MN,又CE⊥MN,MN∥OB,又∠CBN=45,OB=OC,所以∠OBC=∠OCB=∠CBN=∠BCE,所以有 OB=OC=CE=BE 四边形OBEC是正方形,所以OC⊥CE,故CE是⊙O的切线。
(2)因BE=CE,BD=BE+DE,设CE=x,∠D=30,所以CD=2x,DE=x,故有:x+x=2+2 x=2 故圆的半径为2。
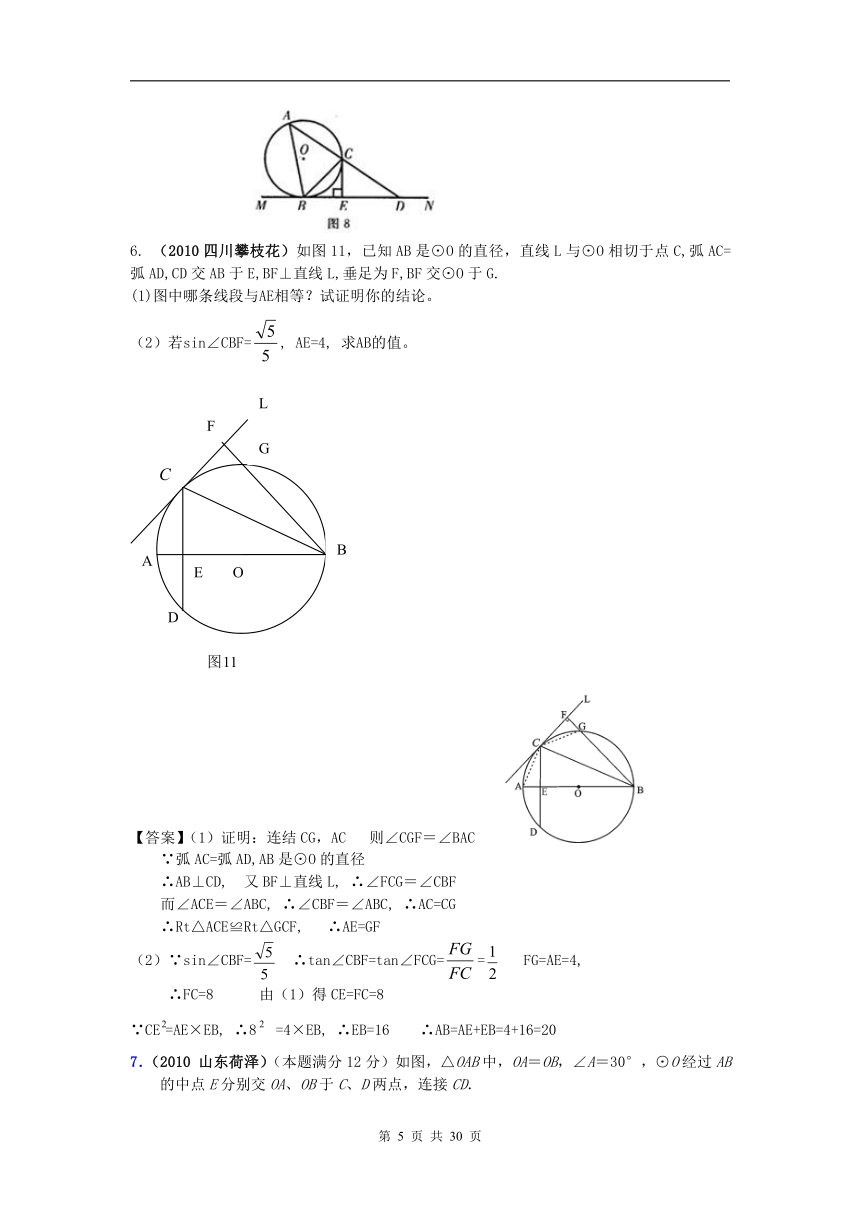
6. (2010四川攀枝花)如图11,已知AB是⊙O的直径,直线L与⊙O相切于点C,弧AC=弧AD,CD交AB于E,BF⊥直线L,垂足为F,BF交⊙O于G.
(1)图中哪条线段与AE相等?试证明你的结论。
(2)若sin∠CBF=, AE=4, 求AB的值。
【答案】(1)证明:连结CG,AC 则∠CGF=∠BAC
∵弧AC=弧AD,AB是⊙O的直径
∴AB⊥CD, 又BF⊥直线L, ∴∠FCG=∠CBF
而∠ACE=∠ABC, ∴∠CBF=∠ABC, ∴AC=CG
∴Rt△ACE≌Rt△GCF, ∴AE=GF
(2)∵sin∠CBF= ∴tan∠CBF=tan∠FCG== FG=AE=4,
∴FC=8 由(1)得CE=FC=8
∵CE=AE×EB, ∴8 =4×EB, ∴EB=16 ∴AB=AE+EB=4+16=20
7.(2010 山东荷泽)(本题满分12分)如图,△OAB中,OA=OB,∠A=30°,⊙O经过AB的中点E分别交OA、OB于C、D两点,连接CD.
⑴求证:AB是⊙O的切线.
⑵求证:CD∥AB.
⑶若CD=,求扇形OCED的面积.
【答案】⑴证明:连接OE,∵OA=OB,E是BC的中点,∴OE⊥AB,∴AB是⊙O的切线。
⑵在△OAB,△OCD中,∠COD=∠AOB,OC=OD,OA=OB,∴∠OCD=∠OAB,
∴CD∥AB
⑶∵CD∥AB,∠A=30°,OE⊥AB,CD=,
∴∠OCD=30°,OE⊥CD,CF=,∠COD=120°,OC==4,
∴S扇形OCED==
8.(2010 湖北咸宁)如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若,求CD的长.
【答案】解:(1)直线FC与⊙O相切.……1分
理由如下:
连接.
∵, ∴……2分
由翻折得,,.
∴. ∴OC∥AF.
∴.
∴直线FC与⊙O相切.……4分
(2)在Rt△OCG中,,
∴.……6分
在Rt△OCE中,.……8分
∵直径AB垂直于弦CD,
∴.……9分
9.(2010 广西钦州市)如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
【答案】解:(1)解法一: 解法二:
∵AB为⊙O的直径, ∵AB为⊙O的直径,∠B=30°,
∴∠ACB=90°.……1分 ∴AC=AB=1,BC=AB cos30°=…2分
∵在Rt△ABC中,∠B=30°,AB=2, ∵弦CD⊥直径AB于点M,
∴BC=AB cos30°=2×.…2分 ∴CD=2CM,AB×CM=AC×BC……4分
∵弦CD⊥直径AB,∠B=30°, ∴CD=2CM=2×
∴ CM=BC=.……4分 =2×=……5分
CD=2CM=.……5分 (其它解法请酌情给分)
(2)证明:∵AE切⊙O于点A,AB为⊙O的直径,
∴∠BAE=90°,∠ACE=∠ACB=90°, 6分
∴∠ACE=∠BAE=90°. 7分
又∵∠E=∠E,
∴Rt△ECA∽Rt△EAB. 8分
∴. 9分
∴AE2=EB EC. 10分
10.(2010鄂尔多斯)如图,AB为⊙O的直径,劣弧,BD∥CE,连接AE并延长交BD于D。
求证:(1)BD是⊙O的切线
(2)
【答案】证明:(1)∵
∴∠1=∠2, AC=AE
∴AB⊥CE
∵CE∥BD ∴AB⊥BD
∴BD是⊙O的切线
(2)连接CB
∵AB是⊙O的切线 ∴∠ACB=90°
∵∠ABD=90°∴∠ACB=∠ABD
∵∠1=∠2∴△ACB∽△ABD
∴ ∴
(证法二,连接BE,证明略)
11.(2010新疆维吾尔自治区新疆建设兵团)如图是一个量角器和一个含30°角的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OE。
(1)求证:DE∥CF;
(2)当OE=2时,若以O、B、F为顶点的三角形与△ABC相似,求OB的长。
(3)若OE=2,移动三角形ABC且使AB边始终与半圆O相切,直角顶点B在直径DE的延长线上移动,求出点B移动的最大距离。
【答案】
解:(1)连结OF
∵AB切半圆O于 F点
∴OF⊥AB
∴∠OFB=∠ABC=90°
∴OF∥BC
∵BC=OE=OF
∴四边形OFCB为平行四边形
∴CF∥OB
即DE∥CF
(2)在Rt△ABC中,∠A=30° BC=OE=2
∴AC=4 AB=
∵△OFB∽△ABC ∴
(3)在Rt△ABC中,BC=OE=2 ∠A=30° 则AC=4
当AB与半圆O相切于E点时,B点与E点重合,BE=0
当AB与半圆O相切于A点时,△OAB≌△CBA OB=AC=4
BE=OB-OE=4-2=2
即点B在直径DE的延长线上移动的最大距离为2.
12.(2010广西梧州)如图,⊙O的直径AC=13,弦BC=12,过点A作直线MN,使∠BAM=∠AOB,
(1)求证:MN是⊙O的切线。
(2)延长CB交MN于点D,求AD的长。
【答案】
(1)证明:∵∠BAM=∠AOB(已知),∠BCA=∠AOB(同弧所对圆周角是圆心角的一半),∴∠BAM=∠BCA(等量代换),
∵∠CBA=90°(直径所对圆周角是直角)∴∠BCA +∠CAB=90°,
∴∠BAM+∠CAB=90°,即:∠CAM=90°∴MN是⊙O的切线。
(2)在Rt△ABC中,AC=13,BC=12,根据勾股定理得:AB=5
∵∠BCA=∠ACD,∠CBA=∠CAD =90°, ∴△DAB∽△CAB,
∴,即:,∴AD=。
13.(2010广西南宁)如图11-①,为⊙的直径,与⊙相切于点,与
⊙相切于点,点为延长线上一点,且.
(1)求证:为⊙的切线;
(2)连接,的延长线与的延长线交于点
(如图11-②所示) .若,求线段和的长.
图11-① 图11-②
【答案】(1)连接 1分
∵
∴
∴ 2分
又∵与⊙相切于点
∴ 3分
∴
∴为⊙的切线 4分
(2)过点作于点,
∵分别切⊙于点
∴ 5分
设为,则,
在中,
解得: 6分
∵ ∴
∵ ∴
∵ ∴
∴ 7分
∴
∴ 8分
解法一:连接,
∴
∴ 9分
在中,
10分
解法二:∵
∴ 9分
∴,,解得 10分14.(2010广东茂名)已知⊙O1的半径为R,周长为C.
(1)在⊙O1内任意作三条弦,其长分别是、、.求证:++< C; (3分)
(2)如图,在直角坐标系O中,设⊙O1的圆心为O1.
①当直线:与⊙O1相切时,求的值;(2分)
②当反比例函数的图象与⊙O1有两个交点时,
求的取值范围. (3分)
:
【答案】(1)证明:,,.++,
因此,++< C.
(2)解:①如图,根据题意可知⊙O1与轴、轴分别相切,设直线与⊙O1相切于点M,则O1M⊥l,过点O1作直线NH⊥轴,与交于点N,与轴交于点H,又∵直线与轴、轴分别交于点E(,0)、F(0,),∴OE=OF=,∴∠NEO=45o,∴∠ENO1=45o,在Rt△O1MN中,O1N=O1Msin45o=,
∴点N的坐标为N(R,),
把点N坐标代入得:,解得:,
②如图,设经过点O、O1的直线交⊙O1于点A、D,则由已知,直线OO1:是圆与反比例函数图象的对称轴,当反比例函数的图象与⊙O1直径AD相交时(点A、D除外),则反比例函数的图象与⊙O1有两个交点.
过点A作AB⊥轴交轴于点B,过O1作O1C⊥轴于点C,OO1=O1Csin45o=,OA=,所以OB=AB=sin45o=,
因此点A的坐标是A,将点A的坐标 代入,解得:.
同理可求得点D的坐标为D,
将点D的坐标代入,解得:
所以当反比例函数的图象与⊙O1有两个交点时,的取值范围是:
15.(2010云南昭通)如图9,已知直线l的解析式为y=-x+6,它与x轴、y轴分别相交于A、B两点,平行于直线l的直线n从原点出发,沿x轴正方向以每秒1个单位长度的速度运动,运动时间为t秒,运动过程中始终保持n∥l,直线n与x轴,y轴分别相交于C、D两点,线段CD的中点为P,以P为圆心,以CD为直径在CD上方作半圆,半圆面积为S,当直线n与直线l重合时,运动结束.
(1)求A、B两点的坐标;
(2)求S与t的函数关系式及自变量t的取值范围;
(3)直线n在运动过程中,
①当t为何值时,半圆与直线l相切?
②是否存在这样的t值,使得半圆面积S=?若存在,求出t值.若不存在,说明理由.
【答案】解:(1)∵y=-x+6,
令y=0,得0=-x+6, x=6.∴A(6,0).
令x=0,得y=6, ∴B(0,6). ……………………2分
(2)∵OA=OB=6,
∴ △AOB是等腰直角三角形.
∵n∥l,
∴∠CDO=∠BAO=45°,
∴ △COD为等腰直角三角形,
OD=OC=t.
CD=
∴.
,
∴. …………………… 8分
(3)①分别过点D、P作DE⊥AB于点E,PF⊥AB于点F.
AD=OA-OD=6-t,
在Rt△ADE中,sin∠EAD=,
DE=,
∴PF= DE=.
当PF=PD时,半圆与l相切.
即,
t=3.
当t=3时,半圆与l相切. ……………………………………11分
②存在.∵.
.
若,则,
,
,
.
∴存在,使得.…………………………14分
16.(2010辽宁大连)如图10,△ABC内接于⊙O的直径,点D在AB的延长线上,
(1)判断DC是否为⊙O的切线,并说明理由;
(2)证明:△AOC≌△DBC
【答案】
17.(2010贵州遵义)如图,在⊿ABC,∠C= 90 °,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC、BC相切于点D、E.
(1)当AC=2时,求⊙O的半径;
(2)设AC=χ,⊙O的半径为y,求y与χ的函数关系式。
【答案】【答案】解法一:连接OD、OE、OC……………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE…………………………………2分
∵S△ABC=S△AOC+S△BOC
∴AC×BC=AC×OD+BC×OE ……………………3分
∵AC+BC=8,AC =2,∴BC=6
∴×2×6=×2×OD+×2×OE ……………………4分
而OD=OE,∴OD=,即⊙O的半径为 ………………5分
解法二:连接OD、OE ………………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE ……………………………2分
∴∠C=90°,∴OECD为正方形
∴OD=OE=EC=CD=t ………………………3分
而△AOD∽△ABC,∴ ………………………4分
∵AC+BC=8,AC =2,∴BC=6,AD=2-t
∴,r=,即⊙O的半径为………………………5分
(2)(7分)连接OD、OE、OC ……………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE=y ………………………2分
S△ABC=S△AOC+S△BOC
∴AC×BC=AC×OD+BC×OE ……………………3分
∵AC+BC=8,AC =x,∴BC=8-x ………………………………4分
x(8-x)=xy+(8-x)y …………………………5分
化简:8x-x2=xy+8y-xy………………………………………6分
即:y=-x2+x ………………………………………………7分
解法二:连接OD、OE ………………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE ………………………2分
∴∠C=90°,∴OECD为正方形
∴OD=OE=EC=CD=y ………………………………3分
由OD∥BC,∴△AOD∽△ABC,
(或者:OD∥AC,∴△OBE∽△ABC)
∴.
∵AC+BC==8,AC=x,
∴BC=8-x,AD=AC-CD=x-y.
∴.
化简得:xy=(x-y)(8-x),
xy=8x-x2-8y+xy.
所以.
解法三:连接OD、OE.
∵D,E是切点,
∴OD⊥AC,OE⊥BC,OD=OE.
∵∠C=90°,∴OECD是正方形.
∴OD=OE=EC=CD=y.
由OD∥BC得:△AOD∽△ABC,
∴,即 ①.
由OE∥AC得:△BOE∽△BAC,
∴,即 ②.
①+②得:,
即.
∴.
18.(2010广东深圳)如图10,以点M(—1,0)为圆心的圆与轴、轴分别交于点A、B、C、D,直线与⊙M相切于点H,交轴于点E,求轴于点F。
(1)请直接写出OE、⊙M的半径r、CH的长;(3分)
(2)如图11,弦HQ交轴于点P,且DP:PH=3:2,求cos∠QHC的值;(3分)
(3)如图12,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交轴于点N。是否存在一个常数,始终满足MN·MK,如果存在,请求出的值;如果不存在,请说明理由。(3分)
【答案】【答案】
(1)、如图①,OE=5,,CH=2
(2)、如图②,连接QC、QD,则,
易知,故,
,,由于,
;
(3)、如图③,连接AK,AM,延长AM,
与圆交于点G,连接TG,则
,
由于,故,;
而,故
在和中,;
故;
;
即:
故存在常数,始终满足
常数
19.(2010广西柳州)如图12,AB为⊙O直径,且弦CD⊥AB于E,过点B的切线与AD的延长线交于点F.
(1)若M是AD的中点,连接ME并延长ME交BC于N.求证:MN⊥BC.
(2)若cos∠C=,DF=3,求⊙O的半径.
【答案】(1)(方法一)
连接AC.
∵ AB为⊙O的直径,且AB⊥CD于E,
由垂径定理:点E是CD的中点. …………1分
又∵ M是AD的中点,
∴ ME是△DAC的中位线.………………2分
∴ MN∥AC.………………………………3分
∵ AB为⊙O的直径,∴ ∠ACB=90°, ………………………………………4分
∴ ∠MNB=90°,即MN⊥BC …………………………………………………5分
(方法二)
∵ AB⊥CD,∴ ∠AED=∠BEC=90° …………………………………………1分
M是AD的中点,∴ ME=AM,即有∠MEA=∠A ……………………………2分
又∵ ∠MEA=∠BEN,由∠A与∠C同对知∠C=∠A
∴ ∠C=∠BEN ……………………………………………………………………3分
又∵ ∠C+∠CBE=90°
∴ ∠CBE+∠BEN=90° ……………………………………………………………4分
∴ ∠BNE=90°,即MN⊥BC …………………………………………………5分
(方法三)
∵ AB⊥CD,∴ ∠AED=90° ……………………………………………………1分
由于M是AD的中点,∴ ME=MD,即有∠MED=∠EDM
又∵ ∠CBE与∠EDA同对
∴ ∠CBE=∠EDA …………………………………………………………………2分
又∵ ∠MED=∠NEC
∴ ∠NEC=∠CBE ………………………………………………………………3分
又∵ ∠C+∠CBE=90°
∴ ∠NEC+∠C=90° ……………………………………………………………4分
即有∠CNE=90°,∴ MN⊥BC …………………………………………………5分
(2)连接BD
∵ ∠BCD与∠BAF同对 ∴ ∠C=∠A
∴ cos∠A=cos∠C= ……………………6分
∵ BF为⊙O的切线 ∴ ∠ABF=90°
在Rt△ABF中,cos∠A=
设AB=4x,则AF=5x,由勾股定理得:BF=3x ……7分
又∵ AB为⊙O的直径,
∴ BD⊥AD
∴ △ABF∽△BDF
∴ ………………………………………………………………………8分
即
……………………………………………………………………………9分
∴ 直径AB=4x=4×
则⊙O的半径为 ………………………………………………………………10分
20.(2010辽宁本溪)已知:如图,在△ABC中,∠A=45°,以AB为直径的⊙O交AC于点D,且AD=DC,CO的延长线交⊙O于点E,过点E作弦EF⊥AB,垂足为点G.
(1)求证:BC是⊙O的切线;
(2)若AB=2,求EF的长.
【答案】
21.(2010辽宁沈阳)如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD。
(1)求证:∠CDE=2∠B;
(2)若BD:AB=,求⊙O的半径及DF的长。
【答案】(1)证明:连接OD………………………1分
∵直线CD与⊙O相切于点D
∴OD⊥CD
∴∠CDO=90°
∴∠CDE+∠ODE=90°……………………2分
又∵DF⊥AB
∴∠DEO=∠DEC=90°
∴∠EOD+∠ODE=90°
∴∠CDE=∠EOD……………………3分
又∵∠EOD=2∠B,∴∠CDE=2∠B……………………4分
(2)解:连接AD
∵AB是⊙O的直径
∴∠ADB=90°……………………5分
∵BD:AB=
∴在直角三角形ADB中,cosB==
∴∠B=30°……………………64分
∴∠AOD=2∠B =60°
又∵∠CDO=90°
∴∠C=30°……………………7分
∵在直角三角形CDO中,CD=10
∴OD=10tan30°=
即⊙O的半径为……………………8分
在直角三角形CDE中,CD=10, ∠=30°
∴DE=CDsin30°=5……………………9分
∵弦DF⊥直径AB于点E
∴DE=EF=DF
∴DF=2DE=10……………………10分
22.(2010 福建莆田)如图,A、B是上的两点,∠AOB=,点D为劣弧 的中点。
(1) 求证:四边形AOBD是菱形;
(2) 延长线段BO至点P,交于另一点C,且BP=3OB,求证;AP是 的切线。
【答案】
23.(2010天门、潜江、仙桃)如图,Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.
(1)求证:;
(2)若BD=3,DE=4,求AE的长.
【答案】(1)设圆心为O,连接OC,则因为∠BCA=90°,所以AB是直径,OB=OC,∴∠OCB=∠OBC,∵∠DBC=∠ABC,∴∠OCB=∠DBC,∴BD∥OC,∴△EOC∽△EBD,∴,即.
(2)在Rt△BDE中,BE==5,因为△EOC∽△EBD,所以,即,r=,所以AE=5-=.
24.(2010广东肇庆)如图7,AB是⊙O的直径,AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP、AE.
求证:
(1)AF//BE;
(2)△ACP∽△FCA;
(3)CP=AE
【答案】证明:(1)∵AB是直径,
∴∠BPA=90°。
∵PF是直径,
∴∠PAF=90°。
∴∠BPA+∠PAF=180°。
∴AF//BE。
(2)∵AC切⊙O于点A,
∴∠CAP=∠AFC。
又∵∠C是公共角,
∴△ACP∽△FCA。
(3)∵AF//BE,
∴∠BPF=∠AFC。
又∵∠CPE=∠BPF,
∴∠CPE=∠AFC。
∵∠CAP=∠AFC。
∴∠CPE=∠CAP。
∴△CPE∽△CAP。
∴=。
∵AB是直径,
∴∠BPA=90°。
∴△AEP∽△BAP。
∴=。
又∵AB=AC,
∴==。
∴CP=AE.
25.(2010云南曲靖)如图,⊙O的直径AB=12,的长为2,D在OC的延长线上,且CD=OC.
(1)求∠A的度数;
(2)求证:DB是⊙O的切线.
(参考公式:弧长公式l=,其中l是弧长,r是半径,n是圆心角度数)
【答案】(1)解:设∠BOC=n0,
据弧长公式,得
n=600.
据圆周角定理,得∠A=.
(2)证明:连接BC,
∵OB=OC,∠BOC=600,
∴△BOC是等边三角形. ∴∠OBC=∠OCB=600,OC=BC=OB
∵OC=CD,
∴BC=CD
∴. ……8分
∴
∴AB⊥BD.
∴DB是⊙O的切线.
26.(2010四川广安)如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
(1) 求证:PC是⊙O的切线;
(2) 点D在劣弧AC什么位置时,才能使,为什么
(3) 在(2)的条件下,若OH=1,AH=2,求弦AC的长.
【答案】(1)连结OC,OC=OA,∴∠OCA=∠OAC,∵PC=PF∴∠PCF=∠PFC,∵∠AFH+∠OAC=90°,∠AFH=∠PFC,∴∠PCF+∠OCA=90°,∴PC是⊙O的切线;
(2)当点D在劣弧AC的中点时有,连结AE、DC,则CD=AD,∠DCA=∠DAC,又∠DCA=∠AED,∴△ADF∽△ADE,∴∴;
(3) 连结OD, OH=1,AH=2,则OA=3,所以DH=,DE=,AD=,由得AF=DF=,又△AHF∽△ABC,∴即,AC的长为。
27.(2010广东湛江) 如图,在△ABC中,以AB为直径的⊙O交BC于点P,PD⊥AC于点D,且PD与⊙O相切.
(1)求证:AB=AC;
(2)若BC=6,AB=4,求CD的值.
【答案】解:(1)证明:连接PO,
因为PD与⊙O相切.所以∠DPO=90°.
因为PD⊥AC,所以∠PDC=∠DPO=90°.
所以OP//OB.
所以∠C=∠OPB.
因为OP=OB,
因为∠OPB=∠B,所以∠C=∠B.所以AB=AC.
(2)解:连接AP,
因为AB是⊙O的直径,所以∠APB=90°.
因为AB=AC,所以∠B=∠C,BP=PC=BC=×6=3.
因为PD⊥AC,所以∠PDC=∠APB=90°.
所以△PDC∽△APB.所以.即.所以CD=.
28.(2010内蒙呼和浩特)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.动点O在边CA上移动,且⊙O的半径为2.
(1)若圆心O与点C重合,则⊙O与直线AB有怎样的位置关系?
(2)当OC等于多少时,⊙O与直线AB相切?
【答案】22.解:(1)作CM⊥AB,垂足为M
在Rt△ABC中,AB===5………………………1分
∵AC·BC=AB·CM
∴CM=………………………2分
∵>2
∴⊙O与直线AB相离………………………3分
(2)如图,设⊙O与AB相切,切点为N,连结ON
则ON⊥AB ∴ON∥CM
∴△AON∽△ACM………………………5分
∴= 设OC=x,则AO=3-x
∴= EQ \f( 2 , ) ∴x=0.5
∴当CO=0.5时,⊙O与直线AB相切………………………7分
29.(2010内蒙赤峰)如图,AB是⊙O的直径,BC是一条弦,连结OC并延长OC至P点,并使PC=BC,∠BOC = 60o
(1)求证:PB是⊙O的切线。
(2)若⊙O的半径长为1,且AB、PB的长是一元二次方程x2+bx+c=0的两个根,求b、c的值。
【答案】(1)证明:在△BOC中,∵OB=OC,∠BOC=60°,
∴∠OBC=∠OCB=∠BOC=60°。 ………………………………………………………2分
又∵PC=BC,∴∠CBP=∠CPB =∠OCB=30°。……………………………………4分
∴∠OBP=∠OBC+∠CBP
=60°+30°=90°,
∴PB⊥AB。
又∵AB是直径,
∴PB是⊙O的切线。……………………………………………………………………6分
(2)∵OB=1, ∴AB=2。
在Rt△POB中,PB= OB·tan60°=………………………………………8分
由题意知x1=2,x2=。∴x1+x2=2+,x1·x2=2。
∴b=,c=2。………………………………………………………………10分
(或将x=2及x=分别代入x2+bx+c=0得
解得结果为不扣分)
30.(2010广西百色)如图1,是⊙的直径,,垂足为,交⊙于点.
(1)用尺规作图:过点作,垂足为(保留作图痕迹,不写作法和证明);
(2)在(1)的条件下,求证:∽;
(3)若点是的中点(如图2),求的值.
【答案】(1)如图 ……………………………2′
(2)证明:∵是⊙直径
∴∠=∠=
∴∠+∠= …………1′
又∵⊥
∴∠=∠=
∴∠+∠= ………………1′
∴∠=∠ ………………1′
∴∽ …………………1′
(3)解:∵∠=,是的中点
∴ 垂直平分 …………………1′
∴ ………………1′
设则
∴= …………1′
∴== ……1′
2
3
1
(第8题)
B
E
D
O
G
C
F
A
(第8题)
B
E
D
O
G
C
F
A
7题图
O
E
D
C
B
A
7题图
O
E
D
C
B
A
H
H
H
M
A
C
P
B
N
O
M
A
C
P
B
N
O
D
P
O
C
B
A
第2题
图②
D
P
O
C
B
A
图①
P
O
C
B
A
O
A
D
P
B
C
D
A
B
C
O
M
N
(第14题(1)图)
(第14题备用图)
(第14题备用图)
C
D
B
图10
A
O
F
图①
图②
F
F
图③
1
OA
A
BA
CA
DA
EA
MA
NA
F
图12
OA
A
BA
CA
DA
EA
MA
NA
F
OA
A
BA
CA
DA
EA
MA
NA
F
A
E
F
G
O
B
C
D
O
C
A
B
P
E
O
F
C
B
O
D
图1
A
图2
A
B
C
D
O
A
B
C
D
O
O
E
F
G
B
D
L
A
图11
第 1 页 共 30 页
解答题
1.(2010 广东汕头)如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.
(1)求∠POA的度数;
(2)计算弦AB的长.
【答案】解:(1)∵PA与⊙O相切于A点
∴OA⊥AP
在Rt△OAP中,由OA=2,OP=4得
∴
∴.
(2)∵弦AB⊥OP,
∴,
∵
∴
∴
∴.
2.(2010 天津)已知是⊙的直径,是⊙的切线,是切点,与⊙交于点.
(Ⅰ)如图①,若,,求的长(结果保留根号);
(Ⅱ)如图②,若为的中点,求证直线是⊙的切线.
【答案】解:(Ⅰ)∵ 是⊙的直径,是切线,
∴ .
在Rt△中,,,
∴ .
由勾股定理,得. ..................5分
(Ⅱ)如图,连接、,
∵ 是⊙的直径,
∴ ,有.
在Rt△中,为的中点,
∴ .
∴ .
又 ∵,
∴.
∵ ,
∴ .
即 .
∴ 直线是⊙的切线.
3.(2010 内蒙古包头)如图,已知是的直径,点在上,过点的直线与的延长线交于点,,.
(1)求证:是的切线;
(2)求证:;
(3)点是的中点,交于点,若,求的值.
【答案】解:(1),
又,
.
又是的直径,
,
,即,
而是的半径,
是的切线.
(2),
,
又,
.
(3)连接,
点是的中点,,,
而,,而,
,,,
又是的直径,,
.
,.
4.(2010广西桂林)如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,
FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.[]
【答案】证明(1)连结OF
∵FH是⊙O的切线
∴OF⊥FH
∵FH∥BC ,
∴OF垂直平分BC
∴
∴AF平分∠BAC
(2)证明:由(1)及题设条件可知
∠1=∠2,∠4=∠3,∠5=∠2
∴∠1+∠4=∠2+∠3
∴∠1+∠4=∠5+∠3
∠FDB=∠FBD
∴BF=FD
(3)解: 在△BFE和△AFB中
∵∠5=∠2=∠1,∠F=∠F
∴△BFE∽△AFB
∴,
∴
∴
∴
∴AD==
5.(2010 广西玉林、防城港)(8分)如图8,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45,过点C的直线与⊙O、MN分别交于A、D两点,过C作CE⊥BD于点E。
(1)求证:CE是⊙O的切线;
(2)若∠D=30,BD=2+2,求⊙O的半径r。
【答案】(1)证明:连接OB,OC,MN是⊙O的切线,所以OB⊥MN,又CE⊥MN,MN∥OB,又∠CBN=45,OB=OC,所以∠OBC=∠OCB=∠CBN=∠BCE,所以有 OB=OC=CE=BE 四边形OBEC是正方形,所以OC⊥CE,故CE是⊙O的切线。
(2)因BE=CE,BD=BE+DE,设CE=x,∠D=30,所以CD=2x,DE=x,故有:x+x=2+2 x=2 故圆的半径为2。
6. (2010四川攀枝花)如图11,已知AB是⊙O的直径,直线L与⊙O相切于点C,弧AC=弧AD,CD交AB于E,BF⊥直线L,垂足为F,BF交⊙O于G.
(1)图中哪条线段与AE相等?试证明你的结论。
(2)若sin∠CBF=, AE=4, 求AB的值。
【答案】(1)证明:连结CG,AC 则∠CGF=∠BAC
∵弧AC=弧AD,AB是⊙O的直径
∴AB⊥CD, 又BF⊥直线L, ∴∠FCG=∠CBF
而∠ACE=∠ABC, ∴∠CBF=∠ABC, ∴AC=CG
∴Rt△ACE≌Rt△GCF, ∴AE=GF
(2)∵sin∠CBF= ∴tan∠CBF=tan∠FCG== FG=AE=4,
∴FC=8 由(1)得CE=FC=8
∵CE=AE×EB, ∴8 =4×EB, ∴EB=16 ∴AB=AE+EB=4+16=20
7.(2010 山东荷泽)(本题满分12分)如图,△OAB中,OA=OB,∠A=30°,⊙O经过AB的中点E分别交OA、OB于C、D两点,连接CD.
⑴求证:AB是⊙O的切线.
⑵求证:CD∥AB.
⑶若CD=,求扇形OCED的面积.
【答案】⑴证明:连接OE,∵OA=OB,E是BC的中点,∴OE⊥AB,∴AB是⊙O的切线。
⑵在△OAB,△OCD中,∠COD=∠AOB,OC=OD,OA=OB,∴∠OCD=∠OAB,
∴CD∥AB
⑶∵CD∥AB,∠A=30°,OE⊥AB,CD=,
∴∠OCD=30°,OE⊥CD,CF=,∠COD=120°,OC==4,
∴S扇形OCED==
8.(2010 湖北咸宁)如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若,求CD的长.
【答案】解:(1)直线FC与⊙O相切.……1分
理由如下:
连接.
∵, ∴……2分
由翻折得,,.
∴. ∴OC∥AF.
∴.
∴直线FC与⊙O相切.……4分
(2)在Rt△OCG中,,
∴.……6分
在Rt△OCE中,.……8分
∵直径AB垂直于弦CD,
∴.……9分
9.(2010 广西钦州市)如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
【答案】解:(1)解法一: 解法二:
∵AB为⊙O的直径, ∵AB为⊙O的直径,∠B=30°,
∴∠ACB=90°.……1分 ∴AC=AB=1,BC=AB cos30°=…2分
∵在Rt△ABC中,∠B=30°,AB=2, ∵弦CD⊥直径AB于点M,
∴BC=AB cos30°=2×.…2分 ∴CD=2CM,AB×CM=AC×BC……4分
∵弦CD⊥直径AB,∠B=30°, ∴CD=2CM=2×
∴ CM=BC=.……4分 =2×=……5分
CD=2CM=.……5分 (其它解法请酌情给分)
(2)证明:∵AE切⊙O于点A,AB为⊙O的直径,
∴∠BAE=90°,∠ACE=∠ACB=90°, 6分
∴∠ACE=∠BAE=90°. 7分
又∵∠E=∠E,
∴Rt△ECA∽Rt△EAB. 8分
∴. 9分
∴AE2=EB EC. 10分
10.(2010鄂尔多斯)如图,AB为⊙O的直径,劣弧,BD∥CE,连接AE并延长交BD于D。
求证:(1)BD是⊙O的切线
(2)
【答案】证明:(1)∵
∴∠1=∠2, AC=AE
∴AB⊥CE
∵CE∥BD ∴AB⊥BD
∴BD是⊙O的切线
(2)连接CB
∵AB是⊙O的切线 ∴∠ACB=90°
∵∠ABD=90°∴∠ACB=∠ABD
∵∠1=∠2∴△ACB∽△ABD
∴ ∴
(证法二,连接BE,证明略)
11.(2010新疆维吾尔自治区新疆建设兵团)如图是一个量角器和一个含30°角的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OE。
(1)求证:DE∥CF;
(2)当OE=2时,若以O、B、F为顶点的三角形与△ABC相似,求OB的长。
(3)若OE=2,移动三角形ABC且使AB边始终与半圆O相切,直角顶点B在直径DE的延长线上移动,求出点B移动的最大距离。
【答案】
解:(1)连结OF
∵AB切半圆O于 F点
∴OF⊥AB
∴∠OFB=∠ABC=90°
∴OF∥BC
∵BC=OE=OF
∴四边形OFCB为平行四边形
∴CF∥OB
即DE∥CF
(2)在Rt△ABC中,∠A=30° BC=OE=2
∴AC=4 AB=
∵△OFB∽△ABC ∴
(3)在Rt△ABC中,BC=OE=2 ∠A=30° 则AC=4
当AB与半圆O相切于E点时,B点与E点重合,BE=0
当AB与半圆O相切于A点时,△OAB≌△CBA OB=AC=4
BE=OB-OE=4-2=2
即点B在直径DE的延长线上移动的最大距离为2.
12.(2010广西梧州)如图,⊙O的直径AC=13,弦BC=12,过点A作直线MN,使∠BAM=∠AOB,
(1)求证:MN是⊙O的切线。
(2)延长CB交MN于点D,求AD的长。
【答案】
(1)证明:∵∠BAM=∠AOB(已知),∠BCA=∠AOB(同弧所对圆周角是圆心角的一半),∴∠BAM=∠BCA(等量代换),
∵∠CBA=90°(直径所对圆周角是直角)∴∠BCA +∠CAB=90°,
∴∠BAM+∠CAB=90°,即:∠CAM=90°∴MN是⊙O的切线。
(2)在Rt△ABC中,AC=13,BC=12,根据勾股定理得:AB=5
∵∠BCA=∠ACD,∠CBA=∠CAD =90°, ∴△DAB∽△CAB,
∴,即:,∴AD=。
13.(2010广西南宁)如图11-①,为⊙的直径,与⊙相切于点,与
⊙相切于点,点为延长线上一点,且.
(1)求证:为⊙的切线;
(2)连接,的延长线与的延长线交于点
(如图11-②所示) .若,求线段和的长.
图11-① 图11-②
【答案】(1)连接 1分
∵
∴
∴ 2分
又∵与⊙相切于点
∴ 3分
∴
∴为⊙的切线 4分
(2)过点作于点,
∵分别切⊙于点
∴ 5分
设为,则,
在中,
解得: 6分
∵ ∴
∵ ∴
∵ ∴
∴ 7分
∴
∴ 8分
解法一:连接,
∴
∴ 9分
在中,
10分
解法二:∵
∴ 9分
∴,,解得 10分14.(2010广东茂名)已知⊙O1的半径为R,周长为C.
(1)在⊙O1内任意作三条弦,其长分别是、、.求证:++< C; (3分)
(2)如图,在直角坐标系O中,设⊙O1的圆心为O1.
①当直线:与⊙O1相切时,求的值;(2分)
②当反比例函数的图象与⊙O1有两个交点时,
求的取值范围. (3分)
:
【答案】(1)证明:,,.++,
因此,++< C.
(2)解:①如图,根据题意可知⊙O1与轴、轴分别相切,设直线与⊙O1相切于点M,则O1M⊥l,过点O1作直线NH⊥轴,与交于点N,与轴交于点H,又∵直线与轴、轴分别交于点E(,0)、F(0,),∴OE=OF=,∴∠NEO=45o,∴∠ENO1=45o,在Rt△O1MN中,O1N=O1Msin45o=,
∴点N的坐标为N(R,),
把点N坐标代入得:,解得:,
②如图,设经过点O、O1的直线交⊙O1于点A、D,则由已知,直线OO1:是圆与反比例函数图象的对称轴,当反比例函数的图象与⊙O1直径AD相交时(点A、D除外),则反比例函数的图象与⊙O1有两个交点.
过点A作AB⊥轴交轴于点B,过O1作O1C⊥轴于点C,OO1=O1Csin45o=,OA=,所以OB=AB=sin45o=,
因此点A的坐标是A,将点A的坐标 代入,解得:.
同理可求得点D的坐标为D,
将点D的坐标代入,解得:
所以当反比例函数的图象与⊙O1有两个交点时,的取值范围是:
15.(2010云南昭通)如图9,已知直线l的解析式为y=-x+6,它与x轴、y轴分别相交于A、B两点,平行于直线l的直线n从原点出发,沿x轴正方向以每秒1个单位长度的速度运动,运动时间为t秒,运动过程中始终保持n∥l,直线n与x轴,y轴分别相交于C、D两点,线段CD的中点为P,以P为圆心,以CD为直径在CD上方作半圆,半圆面积为S,当直线n与直线l重合时,运动结束.
(1)求A、B两点的坐标;
(2)求S与t的函数关系式及自变量t的取值范围;
(3)直线n在运动过程中,
①当t为何值时,半圆与直线l相切?
②是否存在这样的t值,使得半圆面积S=?若存在,求出t值.若不存在,说明理由.
【答案】解:(1)∵y=-x+6,
令y=0,得0=-x+6, x=6.∴A(6,0).
令x=0,得y=6, ∴B(0,6). ……………………2分
(2)∵OA=OB=6,
∴ △AOB是等腰直角三角形.
∵n∥l,
∴∠CDO=∠BAO=45°,
∴ △COD为等腰直角三角形,
OD=OC=t.
CD=
∴.
,
∴. …………………… 8分
(3)①分别过点D、P作DE⊥AB于点E,PF⊥AB于点F.
AD=OA-OD=6-t,
在Rt△ADE中,sin∠EAD=,
DE=,
∴PF= DE=.
当PF=PD时,半圆与l相切.
即,
t=3.
当t=3时,半圆与l相切. ……………………………………11分
②存在.∵.
.
若,则,
,
,
.
∴存在,使得.…………………………14分
16.(2010辽宁大连)如图10,△ABC内接于⊙O的直径,点D在AB的延长线上,
(1)判断DC是否为⊙O的切线,并说明理由;
(2)证明:△AOC≌△DBC
【答案】
17.(2010贵州遵义)如图,在⊿ABC,∠C= 90 °,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC、BC相切于点D、E.
(1)当AC=2时,求⊙O的半径;
(2)设AC=χ,⊙O的半径为y,求y与χ的函数关系式。
【答案】【答案】解法一:连接OD、OE、OC……………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE…………………………………2分
∵S△ABC=S△AOC+S△BOC
∴AC×BC=AC×OD+BC×OE ……………………3分
∵AC+BC=8,AC =2,∴BC=6
∴×2×6=×2×OD+×2×OE ……………………4分
而OD=OE,∴OD=,即⊙O的半径为 ………………5分
解法二:连接OD、OE ………………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE ……………………………2分
∴∠C=90°,∴OECD为正方形
∴OD=OE=EC=CD=t ………………………3分
而△AOD∽△ABC,∴ ………………………4分
∵AC+BC=8,AC =2,∴BC=6,AD=2-t
∴,r=,即⊙O的半径为………………………5分
(2)(7分)连接OD、OE、OC ……………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE=y ………………………2分
S△ABC=S△AOC+S△BOC
∴AC×BC=AC×OD+BC×OE ……………………3分
∵AC+BC=8,AC =x,∴BC=8-x ………………………………4分
x(8-x)=xy+(8-x)y …………………………5分
化简:8x-x2=xy+8y-xy………………………………………6分
即:y=-x2+x ………………………………………………7分
解法二:连接OD、OE ………………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE ………………………2分
∴∠C=90°,∴OECD为正方形
∴OD=OE=EC=CD=y ………………………………3分
由OD∥BC,∴△AOD∽△ABC,
(或者:OD∥AC,∴△OBE∽△ABC)
∴.
∵AC+BC==8,AC=x,
∴BC=8-x,AD=AC-CD=x-y.
∴.
化简得:xy=(x-y)(8-x),
xy=8x-x2-8y+xy.
所以.
解法三:连接OD、OE.
∵D,E是切点,
∴OD⊥AC,OE⊥BC,OD=OE.
∵∠C=90°,∴OECD是正方形.
∴OD=OE=EC=CD=y.
由OD∥BC得:△AOD∽△ABC,
∴,即 ①.
由OE∥AC得:△BOE∽△BAC,
∴,即 ②.
①+②得:,
即.
∴.
18.(2010广东深圳)如图10,以点M(—1,0)为圆心的圆与轴、轴分别交于点A、B、C、D,直线与⊙M相切于点H,交轴于点E,求轴于点F。
(1)请直接写出OE、⊙M的半径r、CH的长;(3分)
(2)如图11,弦HQ交轴于点P,且DP:PH=3:2,求cos∠QHC的值;(3分)
(3)如图12,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交轴于点N。是否存在一个常数,始终满足MN·MK,如果存在,请求出的值;如果不存在,请说明理由。(3分)
【答案】【答案】
(1)、如图①,OE=5,,CH=2
(2)、如图②,连接QC、QD,则,
易知,故,
,,由于,
;
(3)、如图③,连接AK,AM,延长AM,
与圆交于点G,连接TG,则
,
由于,故,;
而,故
在和中,;
故;
;
即:
故存在常数,始终满足
常数
19.(2010广西柳州)如图12,AB为⊙O直径,且弦CD⊥AB于E,过点B的切线与AD的延长线交于点F.
(1)若M是AD的中点,连接ME并延长ME交BC于N.求证:MN⊥BC.
(2)若cos∠C=,DF=3,求⊙O的半径.
【答案】(1)(方法一)
连接AC.
∵ AB为⊙O的直径,且AB⊥CD于E,
由垂径定理:点E是CD的中点. …………1分
又∵ M是AD的中点,
∴ ME是△DAC的中位线.………………2分
∴ MN∥AC.………………………………3分
∵ AB为⊙O的直径,∴ ∠ACB=90°, ………………………………………4分
∴ ∠MNB=90°,即MN⊥BC …………………………………………………5分
(方法二)
∵ AB⊥CD,∴ ∠AED=∠BEC=90° …………………………………………1分
M是AD的中点,∴ ME=AM,即有∠MEA=∠A ……………………………2分
又∵ ∠MEA=∠BEN,由∠A与∠C同对知∠C=∠A
∴ ∠C=∠BEN ……………………………………………………………………3分
又∵ ∠C+∠CBE=90°
∴ ∠CBE+∠BEN=90° ……………………………………………………………4分
∴ ∠BNE=90°,即MN⊥BC …………………………………………………5分
(方法三)
∵ AB⊥CD,∴ ∠AED=90° ……………………………………………………1分
由于M是AD的中点,∴ ME=MD,即有∠MED=∠EDM
又∵ ∠CBE与∠EDA同对
∴ ∠CBE=∠EDA …………………………………………………………………2分
又∵ ∠MED=∠NEC
∴ ∠NEC=∠CBE ………………………………………………………………3分
又∵ ∠C+∠CBE=90°
∴ ∠NEC+∠C=90° ……………………………………………………………4分
即有∠CNE=90°,∴ MN⊥BC …………………………………………………5分
(2)连接BD
∵ ∠BCD与∠BAF同对 ∴ ∠C=∠A
∴ cos∠A=cos∠C= ……………………6分
∵ BF为⊙O的切线 ∴ ∠ABF=90°
在Rt△ABF中,cos∠A=
设AB=4x,则AF=5x,由勾股定理得:BF=3x ……7分
又∵ AB为⊙O的直径,
∴ BD⊥AD
∴ △ABF∽△BDF
∴ ………………………………………………………………………8分
即
……………………………………………………………………………9分
∴ 直径AB=4x=4×
则⊙O的半径为 ………………………………………………………………10分
20.(2010辽宁本溪)已知:如图,在△ABC中,∠A=45°,以AB为直径的⊙O交AC于点D,且AD=DC,CO的延长线交⊙O于点E,过点E作弦EF⊥AB,垂足为点G.
(1)求证:BC是⊙O的切线;
(2)若AB=2,求EF的长.
【答案】
21.(2010辽宁沈阳)如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD。
(1)求证:∠CDE=2∠B;
(2)若BD:AB=,求⊙O的半径及DF的长。
【答案】(1)证明:连接OD………………………1分
∵直线CD与⊙O相切于点D
∴OD⊥CD
∴∠CDO=90°
∴∠CDE+∠ODE=90°……………………2分
又∵DF⊥AB
∴∠DEO=∠DEC=90°
∴∠EOD+∠ODE=90°
∴∠CDE=∠EOD……………………3分
又∵∠EOD=2∠B,∴∠CDE=2∠B……………………4分
(2)解:连接AD
∵AB是⊙O的直径
∴∠ADB=90°……………………5分
∵BD:AB=
∴在直角三角形ADB中,cosB==
∴∠B=30°……………………64分
∴∠AOD=2∠B =60°
又∵∠CDO=90°
∴∠C=30°……………………7分
∵在直角三角形CDO中,CD=10
∴OD=10tan30°=
即⊙O的半径为……………………8分
在直角三角形CDE中,CD=10, ∠=30°
∴DE=CDsin30°=5……………………9分
∵弦DF⊥直径AB于点E
∴DE=EF=DF
∴DF=2DE=10……………………10分
22.(2010 福建莆田)如图,A、B是上的两点,∠AOB=,点D为劣弧 的中点。
(1) 求证:四边形AOBD是菱形;
(2) 延长线段BO至点P,交于另一点C,且BP=3OB,求证;AP是 的切线。
【答案】
23.(2010天门、潜江、仙桃)如图,Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.
(1)求证:;
(2)若BD=3,DE=4,求AE的长.
【答案】(1)设圆心为O,连接OC,则因为∠BCA=90°,所以AB是直径,OB=OC,∴∠OCB=∠OBC,∵∠DBC=∠ABC,∴∠OCB=∠DBC,∴BD∥OC,∴△EOC∽△EBD,∴,即.
(2)在Rt△BDE中,BE==5,因为△EOC∽△EBD,所以,即,r=,所以AE=5-=.
24.(2010广东肇庆)如图7,AB是⊙O的直径,AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP、AE.
求证:
(1)AF//BE;
(2)△ACP∽△FCA;
(3)CP=AE
【答案】证明:(1)∵AB是直径,
∴∠BPA=90°。
∵PF是直径,
∴∠PAF=90°。
∴∠BPA+∠PAF=180°。
∴AF//BE。
(2)∵AC切⊙O于点A,
∴∠CAP=∠AFC。
又∵∠C是公共角,
∴△ACP∽△FCA。
(3)∵AF//BE,
∴∠BPF=∠AFC。
又∵∠CPE=∠BPF,
∴∠CPE=∠AFC。
∵∠CAP=∠AFC。
∴∠CPE=∠CAP。
∴△CPE∽△CAP。
∴=。
∵AB是直径,
∴∠BPA=90°。
∴△AEP∽△BAP。
∴=。
又∵AB=AC,
∴==。
∴CP=AE.
25.(2010云南曲靖)如图,⊙O的直径AB=12,的长为2,D在OC的延长线上,且CD=OC.
(1)求∠A的度数;
(2)求证:DB是⊙O的切线.
(参考公式:弧长公式l=,其中l是弧长,r是半径,n是圆心角度数)
【答案】(1)解:设∠BOC=n0,
据弧长公式,得
n=600.
据圆周角定理,得∠A=.
(2)证明:连接BC,
∵OB=OC,∠BOC=600,
∴△BOC是等边三角形. ∴∠OBC=∠OCB=600,OC=BC=OB
∵OC=CD,
∴BC=CD
∴. ……8分
∴
∴AB⊥BD.
∴DB是⊙O的切线.
26.(2010四川广安)如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
(1) 求证:PC是⊙O的切线;
(2) 点D在劣弧AC什么位置时,才能使,为什么
(3) 在(2)的条件下,若OH=1,AH=2,求弦AC的长.
【答案】(1)连结OC,OC=OA,∴∠OCA=∠OAC,∵PC=PF∴∠PCF=∠PFC,∵∠AFH+∠OAC=90°,∠AFH=∠PFC,∴∠PCF+∠OCA=90°,∴PC是⊙O的切线;
(2)当点D在劣弧AC的中点时有,连结AE、DC,则CD=AD,∠DCA=∠DAC,又∠DCA=∠AED,∴△ADF∽△ADE,∴∴;
(3) 连结OD, OH=1,AH=2,则OA=3,所以DH=,DE=,AD=,由得AF=DF=,又△AHF∽△ABC,∴即,AC的长为。
27.(2010广东湛江) 如图,在△ABC中,以AB为直径的⊙O交BC于点P,PD⊥AC于点D,且PD与⊙O相切.
(1)求证:AB=AC;
(2)若BC=6,AB=4,求CD的值.
【答案】解:(1)证明:连接PO,
因为PD与⊙O相切.所以∠DPO=90°.
因为PD⊥AC,所以∠PDC=∠DPO=90°.
所以OP//OB.
所以∠C=∠OPB.
因为OP=OB,
因为∠OPB=∠B,所以∠C=∠B.所以AB=AC.
(2)解:连接AP,
因为AB是⊙O的直径,所以∠APB=90°.
因为AB=AC,所以∠B=∠C,BP=PC=BC=×6=3.
因为PD⊥AC,所以∠PDC=∠APB=90°.
所以△PDC∽△APB.所以.即.所以CD=.
28.(2010内蒙呼和浩特)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.动点O在边CA上移动,且⊙O的半径为2.
(1)若圆心O与点C重合,则⊙O与直线AB有怎样的位置关系?
(2)当OC等于多少时,⊙O与直线AB相切?
【答案】22.解:(1)作CM⊥AB,垂足为M
在Rt△ABC中,AB===5………………………1分
∵AC·BC=AB·CM
∴CM=………………………2分
∵>2
∴⊙O与直线AB相离………………………3分
(2)如图,设⊙O与AB相切,切点为N,连结ON
则ON⊥AB ∴ON∥CM
∴△AON∽△ACM………………………5分
∴= 设OC=x,则AO=3-x
∴= EQ \f( 2 , ) ∴x=0.5
∴当CO=0.5时,⊙O与直线AB相切………………………7分
29.(2010内蒙赤峰)如图,AB是⊙O的直径,BC是一条弦,连结OC并延长OC至P点,并使PC=BC,∠BOC = 60o
(1)求证:PB是⊙O的切线。
(2)若⊙O的半径长为1,且AB、PB的长是一元二次方程x2+bx+c=0的两个根,求b、c的值。
【答案】(1)证明:在△BOC中,∵OB=OC,∠BOC=60°,
∴∠OBC=∠OCB=∠BOC=60°。 ………………………………………………………2分
又∵PC=BC,∴∠CBP=∠CPB =∠OCB=30°。……………………………………4分
∴∠OBP=∠OBC+∠CBP
=60°+30°=90°,
∴PB⊥AB。
又∵AB是直径,
∴PB是⊙O的切线。……………………………………………………………………6分
(2)∵OB=1, ∴AB=2。
在Rt△POB中,PB= OB·tan60°=………………………………………8分
由题意知x1=2,x2=。∴x1+x2=2+,x1·x2=2。
∴b=,c=2。………………………………………………………………10分
(或将x=2及x=分别代入x2+bx+c=0得
解得结果为不扣分)
30.(2010广西百色)如图1,是⊙的直径,,垂足为,交⊙于点.
(1)用尺规作图:过点作,垂足为(保留作图痕迹,不写作法和证明);
(2)在(1)的条件下,求证:∽;
(3)若点是的中点(如图2),求的值.
【答案】(1)如图 ……………………………2′
(2)证明:∵是⊙直径
∴∠=∠=
∴∠+∠= …………1′
又∵⊥
∴∠=∠=
∴∠+∠= ………………1′
∴∠=∠ ………………1′
∴∽ …………………1′
(3)解:∵∠=,是的中点
∴ 垂直平分 …………………1′
∴ ………………1′
设则
∴= …………1′
∴== ……1′
2
3
1
(第8题)
B
E
D
O
G
C
F
A
(第8题)
B
E
D
O
G
C
F
A
7题图
O
E
D
C
B
A
7题图
O
E
D
C
B
A
H
H
H
M
A
C
P
B
N
O
M
A
C
P
B
N
O
D
P
O
C
B
A
第2题
图②
D
P
O
C
B
A
图①
P
O
C
B
A
O
A
D
P
B
C
D
A
B
C
O
M
N
(第14题(1)图)
(第14题备用图)
(第14题备用图)
C
D
B
图10
A
O
F
图①
图②
F
F
图③
1
OA
A
BA
CA
DA
EA
MA
NA
F
图12
OA
A
BA
CA
DA
EA
MA
NA
F
OA
A
BA
CA
DA
EA
MA
NA
F
A
E
F
G
O
B
C
D
O
C
A
B
P
E
O
F
C
B
O
D
图1
A
图2
A
B
C
D
O
A
B
C
D
O
O
E
F
G
B
D
L
A
图11
第 1 页 共 30 页
同课章节目录
