1.1 探索勾股定理(2)(北师大8上)
文档属性
| 名称 | 1.1 探索勾股定理(2)(北师大8上) | 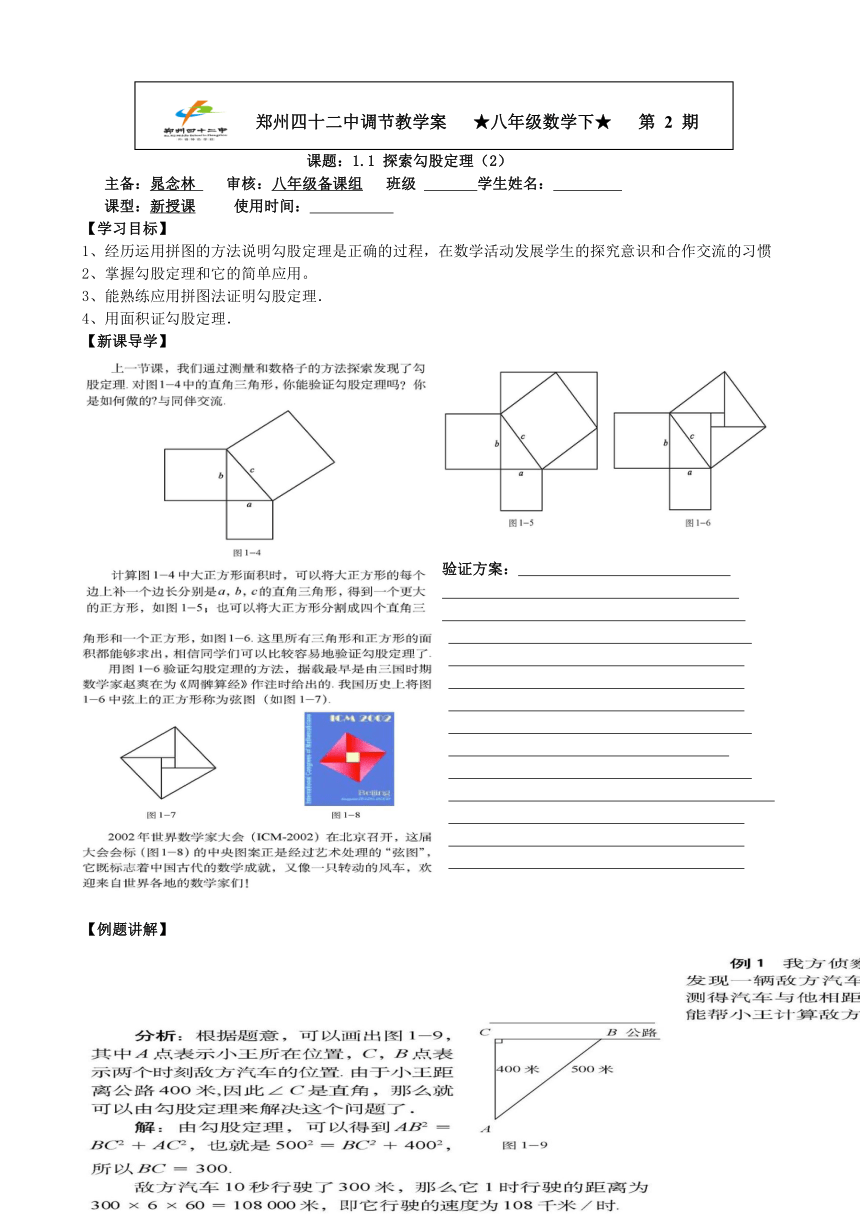 | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-19 11:20:00 | ||
图片预览


文档简介
课题:1.1 探索勾股定理(2)
主备:晁念林 审核:八年级备课组 班级 学生姓名:
课型:新授课 使用时间:
【学习目标】
1、经历运用拼图的方法说明勾股定理是正确的过程,在数学活动发展学生的探究意识和合作交流的习惯
2、掌握勾股定理和它的简单应用。
3、能熟练应用拼图法证明勾股定理.
4、用面积证勾股定理.
【新课导学】
验证方案:
【例题讲解】
例2、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000 米处,过了 20 秒,飞机距离这个男孩头顶5000米,飞机每时飞行多少千米?
分析:根据题意,可以先画出符合题意的图形。如右图,图中△ABC的∠C=90°,AC = 4000米,AB=5000 米欲求飞机每时飞行多少千米,就要知道20 秒时间里飞行的路程,即图中的CB的长,由于△ ABC的斜边AB =5000米,AC= 4000 米,这样BC就可以通过勾股定理得出,这里一定要注意单位的换算。
解:由勾股定理得
即 BC=3千米
飞机 20秒飞行3 千米.那么它 l 小时飞行的距离为:
(千米/时)
答:飞机每小时飞行 540千米。
【自我检测】
2、在△ABC中,∠C=900,,BC=60cm,CA=80cm,一只蜗牛从C点出发,以每分20cm的速度沿CA-AB-BC的路径再回到C点,需要______分的时间.
3、如图,四边形是正方形,垂直于,且=3,=4,阴影部分的面积是______
4、如图,要从电线杆离地面8m处向地面拉一条长10m的电缆,求地面电缆固定点A到电线杆底部B的距离.
【形成性检测】:
1、如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲
到达点B200m,结果他在水中实际游了520m,求该河流的宽度为_________。
2、小明把一根70cm长的木棒放到一个长、宽、高分别为30cm、40cm、50cm的木箱中,他能放进去吗?答:_______________(填“能”、或“不能”)
3、如图,∠OAB=∠OBC=∠OCD=90°, AB=BC=CD=1,OA=2,则OD2=____________.
4、直角三角形两直角边长分别为6cm和8cm,则连接这两条直角边中点的线段长为 ( )
(A) 10cm (B) 3cm (C) 4cm (D) 5cm
5、如图,在水塔O的东北方向处有一抽水站,在水塔的东南方向处有一建筑工地,在间建一条直水管,则水管的长为( )
(A) (B) (C) (D)
6、如图,在边长为的正方形中挖掉一个边长为的小正方形,余下的部分拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式。则这个等式是( )
(A)
(B)
(C)
(D)
7、如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b.利用这个图试说明勾股定理
【课堂小结】
1、 本节课你的收获是:
2、
3、 本节课你遇到的困难是:
4、
3、你是怎样解决这些困难的:
【今日作业】
1、如图,已知直角三角形ABC的两直角边AC,BC的长分别为4cm,3cm,求斜边AB上的高CD的长.
3、一游泳池长48cm,小方和小朱进行游泳比赛,从同一处出发,小方平均速度为3m/秒,小朱为3.1m/秒.但小朱一心想快,不看方向沿斜线游,而小方直游,俩人到达终点的位置相距14m.按各人的平均速度计算,谁先到达终点,为什么?
【学习心得】
郑州四十二中调节教学案 ★八年级数学下★ 第 2 期
第7题图
C
主备:晁念林 审核:八年级备课组 班级 学生姓名:
课型:新授课 使用时间:
【学习目标】
1、经历运用拼图的方法说明勾股定理是正确的过程,在数学活动发展学生的探究意识和合作交流的习惯
2、掌握勾股定理和它的简单应用。
3、能熟练应用拼图法证明勾股定理.
4、用面积证勾股定理.
【新课导学】
验证方案:
【例题讲解】
例2、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000 米处,过了 20 秒,飞机距离这个男孩头顶5000米,飞机每时飞行多少千米?
分析:根据题意,可以先画出符合题意的图形。如右图,图中△ABC的∠C=90°,AC = 4000米,AB=5000 米欲求飞机每时飞行多少千米,就要知道20 秒时间里飞行的路程,即图中的CB的长,由于△ ABC的斜边AB =5000米,AC= 4000 米,这样BC就可以通过勾股定理得出,这里一定要注意单位的换算。
解:由勾股定理得
即 BC=3千米
飞机 20秒飞行3 千米.那么它 l 小时飞行的距离为:
(千米/时)
答:飞机每小时飞行 540千米。
【自我检测】
2、在△ABC中,∠C=900,,BC=60cm,CA=80cm,一只蜗牛从C点出发,以每分20cm的速度沿CA-AB-BC的路径再回到C点,需要______分的时间.
3、如图,四边形是正方形,垂直于,且=3,=4,阴影部分的面积是______
4、如图,要从电线杆离地面8m处向地面拉一条长10m的电缆,求地面电缆固定点A到电线杆底部B的距离.
【形成性检测】:
1、如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲
到达点B200m,结果他在水中实际游了520m,求该河流的宽度为_________。
2、小明把一根70cm长的木棒放到一个长、宽、高分别为30cm、40cm、50cm的木箱中,他能放进去吗?答:_______________(填“能”、或“不能”)
3、如图,∠OAB=∠OBC=∠OCD=90°, AB=BC=CD=1,OA=2,则OD2=____________.
4、直角三角形两直角边长分别为6cm和8cm,则连接这两条直角边中点的线段长为 ( )
(A) 10cm (B) 3cm (C) 4cm (D) 5cm
5、如图,在水塔O的东北方向处有一抽水站,在水塔的东南方向处有一建筑工地,在间建一条直水管,则水管的长为( )
(A) (B) (C) (D)
6、如图,在边长为的正方形中挖掉一个边长为的小正方形,余下的部分拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式。则这个等式是( )
(A)
(B)
(C)
(D)
7、如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b.利用这个图试说明勾股定理
【课堂小结】
1、 本节课你的收获是:
2、
3、 本节课你遇到的困难是:
4、
3、你是怎样解决这些困难的:
【今日作业】
1、如图,已知直角三角形ABC的两直角边AC,BC的长分别为4cm,3cm,求斜边AB上的高CD的长.
3、一游泳池长48cm,小方和小朱进行游泳比赛,从同一处出发,小方平均速度为3m/秒,小朱为3.1m/秒.但小朱一心想快,不看方向沿斜线游,而小方直游,俩人到达终点的位置相距14m.按各人的平均速度计算,谁先到达终点,为什么?
【学习心得】
郑州四十二中调节教学案 ★八年级数学下★ 第 2 期
第7题图
C
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
