新课标A版必修1函数的奇偶性
图片预览





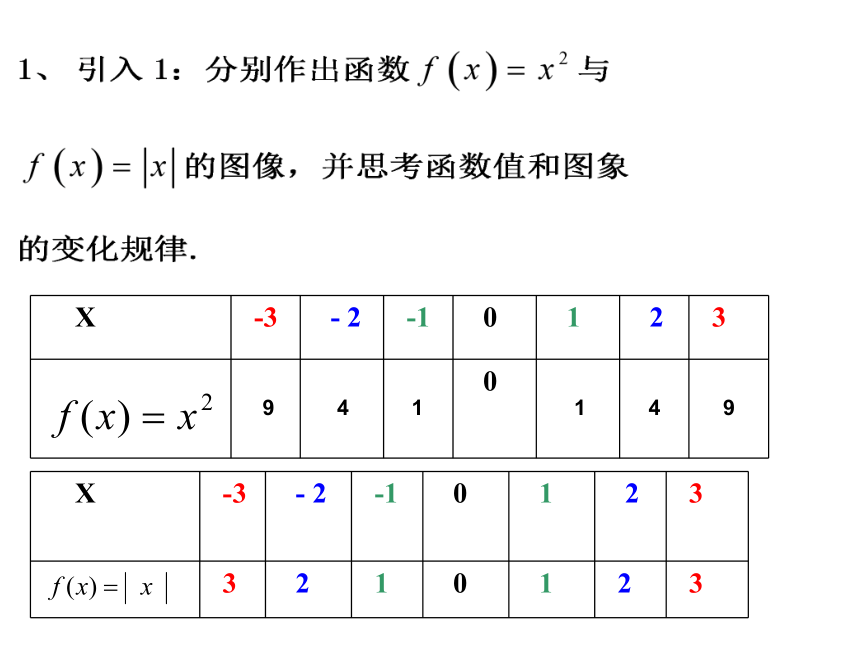

文档简介
课件17张PPT。复习:
(一)复合函数单调性2.3.2 函数的奇偶性 1 1 4 4 9 9 1 1 2 -2 3-3 4、奇函数定义:一般地,如果对于函数f (x)的
定义域内任意一个x,都有f (-x)=-f (x),
那么函数f (x)就叫做奇函数(odd fun_ction).结论:(1)一般函数的奇偶性有四种:奇函数、偶函数、既奇且偶函数、非奇非偶函数,一个函数是奇函数或是偶函数叫这个函数具有奇偶性,
显然函数的奇偶性是相对于函数的整个定义或二言,而非相对于某个区间。(2)若f (x)是奇函数或偶函数,则对于定义域D上的任意一个x,
都有-x∈D,这就是定义域必须是关于原点对称的.若函数的定
义域不是关于原点对称的,则可判断该函数既不是奇函数又不是
偶函数.定理:奇函数、偶函数的图象的对称性
①奇函数的图象关于原点对称,反之,
若一个函数的图象关于原点对称,则这个函数是奇函数.
②偶函数的图象关于y轴对称,反之,
若一个函数的图象关于y轴对称,则这个函数是偶函数.练习:P36 2作业本:1.3.2
课外作业:成材之路:P 35 1.3.2 ; 背面1.3.2;P44 A:10 ; B:6
(一)复合函数单调性2.3.2 函数的奇偶性 1 1 4 4 9 9 1 1 2 -2 3-3 4、奇函数定义:一般地,如果对于函数f (x)的
定义域内任意一个x,都有f (-x)=-f (x),
那么函数f (x)就叫做奇函数(odd fun_ction).结论:(1)一般函数的奇偶性有四种:奇函数、偶函数、既奇且偶函数、非奇非偶函数,一个函数是奇函数或是偶函数叫这个函数具有奇偶性,
显然函数的奇偶性是相对于函数的整个定义或二言,而非相对于某个区间。(2)若f (x)是奇函数或偶函数,则对于定义域D上的任意一个x,
都有-x∈D,这就是定义域必须是关于原点对称的.若函数的定
义域不是关于原点对称的,则可判断该函数既不是奇函数又不是
偶函数.定理:奇函数、偶函数的图象的对称性
①奇函数的图象关于原点对称,反之,
若一个函数的图象关于原点对称,则这个函数是奇函数.
②偶函数的图象关于y轴对称,反之,
若一个函数的图象关于y轴对称,则这个函数是偶函数.练习:P36 2作业本:1.3.2
课外作业:成材之路:P 35 1.3.2 ; 背面1.3.2;P44 A:10 ; B:6
