(北师大版必修4)数学:1.1周期现象与周期函数(同步练习)
文档属性
| 名称 | (北师大版必修4)数学:1.1周期现象与周期函数(同步练习) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-19 00:00:00 | ||
图片预览



文档简介
第一章 三角函数练习 同步练习(一)
选择题
1.若=1,则对任意正整数n,的取值为( )21世纪教育网
A.1 ?B.区间(0,1) C.2:3 D.不能确定
2.已知,则的图象是下图中的( )
3.下列各对函数值符号相同是的( )
A., B.,
C., D.,
4.下列四个不等式中,,错误的个数是( )
A.0 B.1 C.2 D.3
5.若,且<<,则的值的等于( )
A. B. C.- D.
6.函数在下列区间上是增函数的是( )
A.[-,] B.[-,] C. D.[-,]
7.函数的图象可以看成是把函数的图象做以下平移得到( )
A.左平移 B.右平移 C.左平移 D.右平移
8. 等于( )
A.0 B.1 C.-1 D.
9.按照下列方式排列,周期是_________,第100个位置是_________.
10.试举出在日常生活中5个周期现象的例子.
11.若与的单调性相反,则在第_________象限。
12.是以4π为周期的函数,当时,,则.
13.函数的定义域是________.
14.已知角的终边在函数是图像上,则.
15.已知,则….
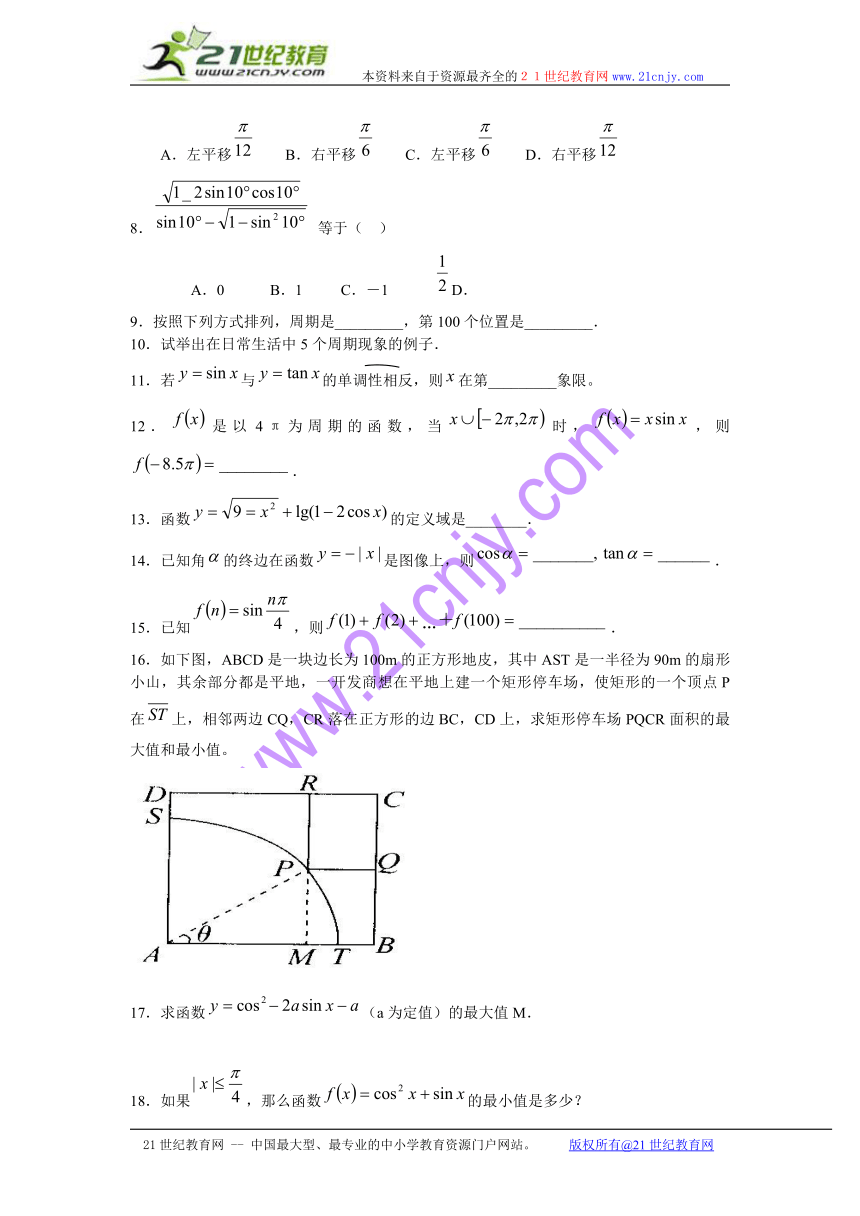
16.如下图,ABCD是一块边长为100m的正方形地皮,其中AST是一半径为90m的扇形小山,其余部分都是平地,一开发商想在平地上建一个矩形停车场,使矩形的一个顶点P在上,相邻两边CQ,CR落在正方形的边BC,CD上,求矩形停车场PQCR面积的最大值和最小值。
17.求函数(a为定值)的最大值M.
18.如果,那么函数的最小值是多少?
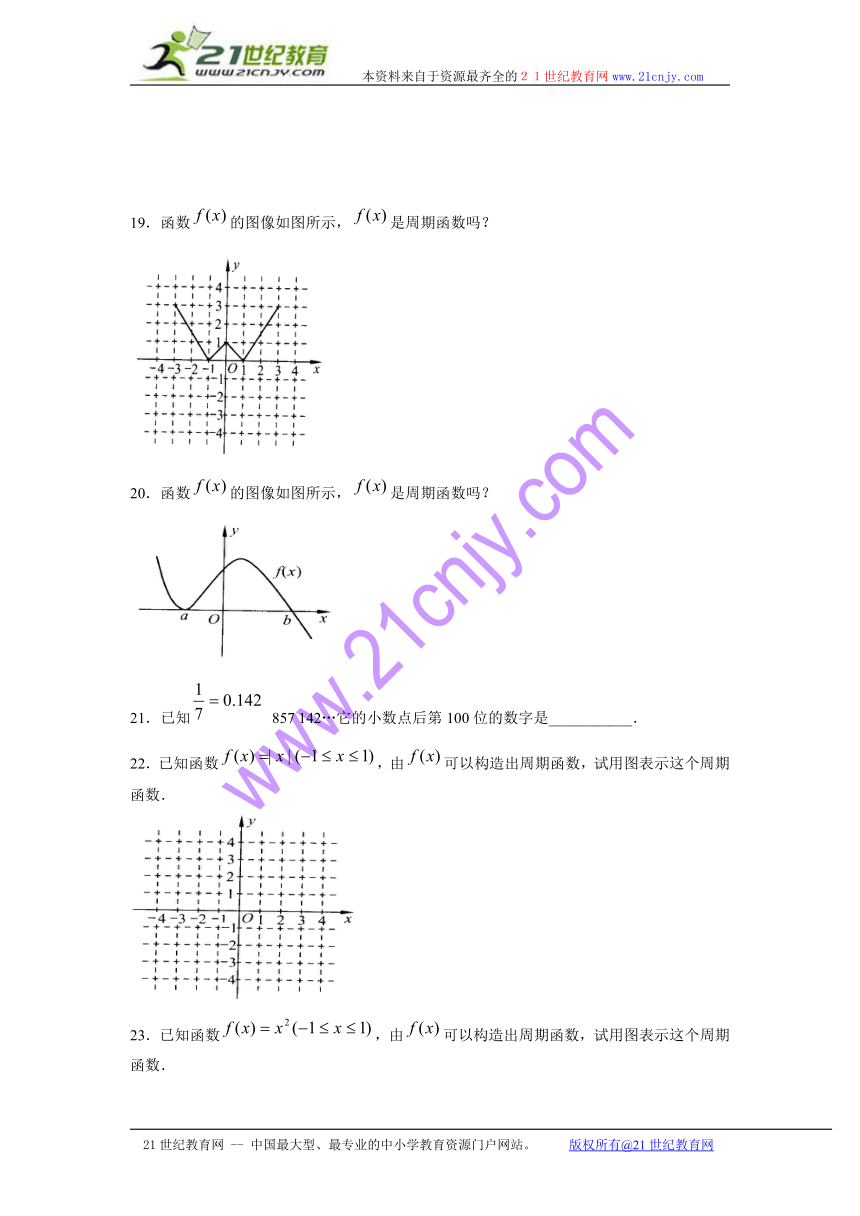
19.函数的图像如图所示,是周期函数吗?
20.函数的图像如图所示,是周期函数吗?
21.已知 857 142…它的小数点后第100位的数字是___________.
22.已知函数,由可以构造出周期函数,试用图表示这个周期函数.
23.已知函数,由可以构造出周期函数,试用图表示这个周期函数.
24.证明是非周期函数.
25.终边在轴上的角的集合是_____________.
26.与-终边相同的角的集合是____________.
27.在~范围内,与角-18'终边相同的角是___________.
28.写出与下列各角终边相同的角的集合,并把集合中适合不等式-的元素写出来.
(1); (2); (3)-15'
29.第一象限的角的集合S是_____________.
30.如果是锐角,试说明所在的象限.
31.如果角与角的终边在同一条直线上,试问角与角有什么关系?
32.30'化为弧度制是___________.
33.-化成角度是___________.
34.扇形的中心角为,弧长为,则其内切圆的半径________.
35.把下列各角化成0~的角加上的形式,并指出它们是哪个象限的角.
(1) (2)-2
36.与-终边相同的最小正角是________.
37.求下列各式的值:
(1) (2) (3)
38.半径为20m的车轮为4rad/s的速度旋转,求轮上一点经过10 s所转过的弧长.
39.已知角终边经过点P(4,-5),则=_________.
40.求下列正弦值:
(1); (2); (3).
41.为什么?21世纪教育网
42、若角的终边落在直线上,求的值.
43、已知点P(a,2)是角终边上一点,且=,求a的值.
44、用定义证明:.
45.函数的图像与直线有_________交点.
46.在同一坐标系中画出下面两个函数的图像,其中.
(1); (2)
47.计算:.
48.化简:.
49. 函数与函数的图像有_____交点.
50.如果,那么是第__________象限的角.
51.根据函数的图像,写出使成立的的取值集合.
52.函数的单调递增区间是___________.
53.函数的定义域是__________.
54.求函数的最大值和最小值,并写出使函数最大值和最小值时的自变量 的集合.
21世纪教育网
55.比价下列各组数的大小:
(1)与; (2)与.
56.函数的定义域是_________.
57.判断下列函数的奇偶性:
(1); (2);
(3); (4).
58.研究方程的根的个数.
答案:
1、A 2、C 3、B 4、A 5、C
6、B 7、A 8、C
9、
10、
11、二或第三 12、
19、不是 20、不是
21、8
22、如图
23、如图
24、
25、
26、
27、
28、
29、
30、
31、
32、 33、-450° 34、3
35、
36、
37、(1) (2) (3)
38、
39、
40、(1) (2) (3)
41、
42、
43、[来源:21世纪教育网]
44、
45、一个
46、略
47、
48、
49、一 50、三,四
51、
52、
[来源:21世纪教育网]
53、R
54、
55、
56、
57、
58、
59、
选择题
1.若=1,则对任意正整数n,的取值为( )21世纪教育网
A.1 ?B.区间(0,1) C.2:3 D.不能确定
2.已知,则的图象是下图中的( )
3.下列各对函数值符号相同是的( )
A., B.,
C., D.,
4.下列四个不等式中,,错误的个数是( )
A.0 B.1 C.2 D.3
5.若,且<<,则的值的等于( )
A. B. C.- D.
6.函数在下列区间上是增函数的是( )
A.[-,] B.[-,] C. D.[-,]
7.函数的图象可以看成是把函数的图象做以下平移得到( )
A.左平移 B.右平移 C.左平移 D.右平移
8. 等于( )
A.0 B.1 C.-1 D.
9.按照下列方式排列,周期是_________,第100个位置是_________.
10.试举出在日常生活中5个周期现象的例子.
11.若与的单调性相反,则在第_________象限。
12.是以4π为周期的函数,当时,,则.
13.函数的定义域是________.
14.已知角的终边在函数是图像上,则.
15.已知,则….
16.如下图,ABCD是一块边长为100m的正方形地皮,其中AST是一半径为90m的扇形小山,其余部分都是平地,一开发商想在平地上建一个矩形停车场,使矩形的一个顶点P在上,相邻两边CQ,CR落在正方形的边BC,CD上,求矩形停车场PQCR面积的最大值和最小值。
17.求函数(a为定值)的最大值M.
18.如果,那么函数的最小值是多少?
19.函数的图像如图所示,是周期函数吗?
20.函数的图像如图所示,是周期函数吗?
21.已知 857 142…它的小数点后第100位的数字是___________.
22.已知函数,由可以构造出周期函数,试用图表示这个周期函数.
23.已知函数,由可以构造出周期函数,试用图表示这个周期函数.
24.证明是非周期函数.
25.终边在轴上的角的集合是_____________.
26.与-终边相同的角的集合是____________.
27.在~范围内,与角-18'终边相同的角是___________.
28.写出与下列各角终边相同的角的集合,并把集合中适合不等式-的元素写出来.
(1); (2); (3)-15'
29.第一象限的角的集合S是_____________.
30.如果是锐角,试说明所在的象限.
31.如果角与角的终边在同一条直线上,试问角与角有什么关系?
32.30'化为弧度制是___________.
33.-化成角度是___________.
34.扇形的中心角为,弧长为,则其内切圆的半径________.
35.把下列各角化成0~的角加上的形式,并指出它们是哪个象限的角.
(1) (2)-2
36.与-终边相同的最小正角是________.
37.求下列各式的值:
(1) (2) (3)
38.半径为20m的车轮为4rad/s的速度旋转,求轮上一点经过10 s所转过的弧长.
39.已知角终边经过点P(4,-5),则=_________.
40.求下列正弦值:
(1); (2); (3).
41.为什么?21世纪教育网
42、若角的终边落在直线上,求的值.
43、已知点P(a,2)是角终边上一点,且=,求a的值.
44、用定义证明:.
45.函数的图像与直线有_________交点.
46.在同一坐标系中画出下面两个函数的图像,其中.
(1); (2)
47.计算:.
48.化简:.
49. 函数与函数的图像有_____交点.
50.如果,那么是第__________象限的角.
51.根据函数的图像,写出使成立的的取值集合.
52.函数的单调递增区间是___________.
53.函数的定义域是__________.
54.求函数的最大值和最小值,并写出使函数最大值和最小值时的自变量 的集合.
21世纪教育网
55.比价下列各组数的大小:
(1)与; (2)与.
56.函数的定义域是_________.
57.判断下列函数的奇偶性:
(1); (2);
(3); (4).
58.研究方程的根的个数.
答案:
1、A 2、C 3、B 4、A 5、C
6、B 7、A 8、C
9、
10、
11、二或第三 12、
19、不是 20、不是
21、8
22、如图
23、如图
24、
25、
26、
27、
28、
29、
30、
31、
32、 33、-450° 34、3
35、
36、
37、(1) (2) (3)
38、
39、
40、(1) (2) (3)
41、
42、
43、[来源:21世纪教育网]
44、
45、一个
46、略
47、
48、
49、一 50、三,四
51、
52、
[来源:21世纪教育网]
53、R
54、
55、
56、
57、
58、
59、
