28.2 解直角三角形(第1课时)
文档属性
| 名称 | 28.2 解直角三角形(第1课时) |  | |
| 格式 | rar | ||
| 文件大小 | 383.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-20 12:32:00 | ||
图片预览





文档简介
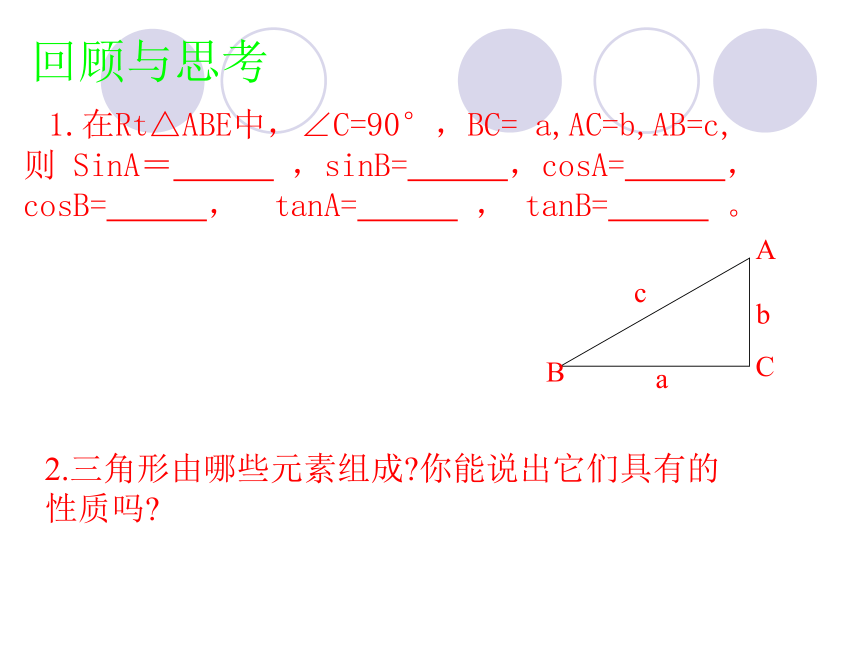
课件15张PPT。28.2 解直角三角形(第1课时)回顾与思考1.在Rt△ABE中,∠C=90°,BC= a,AC=b,AB=c,则 SinA= ,sinB= ,cosA= , cosB= , tanA= , tanB= 。
2.三角形由哪些元素组成?你能说出它们具有的性质吗?解直角三角形问题: 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角a一般要满足50°≤a≤75°.现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角a等于多少(精确到1°)?这时人是否能够安全使用这个梯子?想一想问题(1)可以归结为:在Rt △ABC中,已知∠A=75°,斜边AB=6,求∠A的对边BC的长. 问题(1)当梯子与地面所成的角a为75°时,梯子顶端与地面的距离是使用这个梯子所能攀到的最大高度.对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的角a的问题,可以归结为:在Rt△ABC中,已知AC=2.4,斜边AB=6,求锐角a的度数在图中的Rt△ABC中,
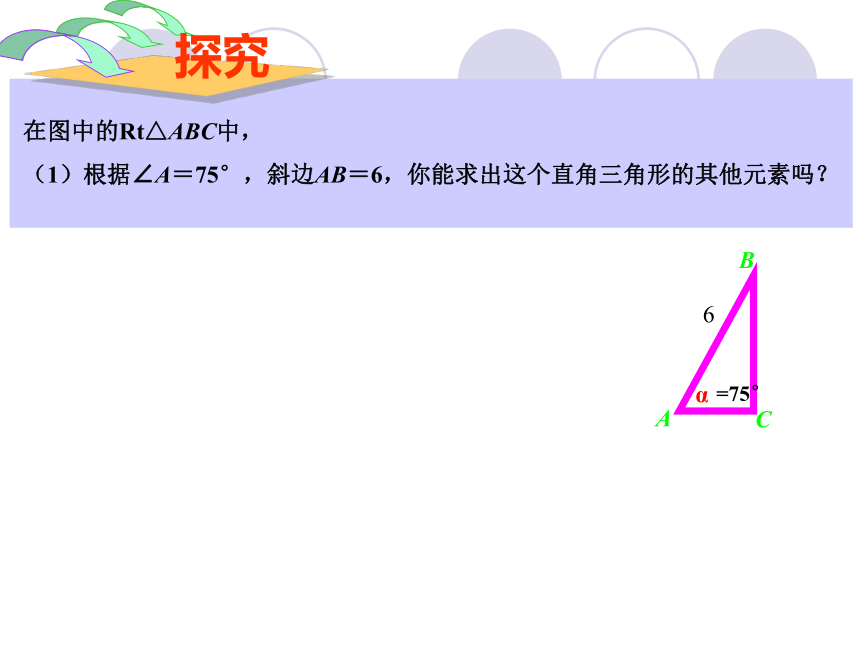
(1)根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?6=75°在图中的Rt△ABC中,
(2)根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?62.4解直角三角形:在直角三角形中,由已知元素求未知元素的过程.什么是解直角三角形(2)两锐角之间的关系∠A+∠B=90°(3)边角之间的关系(1)三边之间的关系 (勾股定理)在解直角三角形的过程中,一般要用到下面一些关系:
如何解直角三角形你还有其他方法求出c吗?
如何解直角三角形 根据以上条件可以求出塔身中心线与垂直中心线的夹角.你愿意试着计算一下吗?解决有关比萨斜塔倾斜的问题. 在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 30 , b = 20 ;练习 (2) ∠B=72°,c = 14.名言: 聪明在于学习,天才在于积累。……所谓天才,实际上是依靠学习。_____华罗庚
2.三角形由哪些元素组成?你能说出它们具有的性质吗?解直角三角形问题: 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角a一般要满足50°≤a≤75°.现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角a等于多少(精确到1°)?这时人是否能够安全使用这个梯子?想一想问题(1)可以归结为:在Rt △ABC中,已知∠A=75°,斜边AB=6,求∠A的对边BC的长. 问题(1)当梯子与地面所成的角a为75°时,梯子顶端与地面的距离是使用这个梯子所能攀到的最大高度.对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的角a的问题,可以归结为:在Rt△ABC中,已知AC=2.4,斜边AB=6,求锐角a的度数在图中的Rt△ABC中,
(1)根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?6=75°在图中的Rt△ABC中,
(2)根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?62.4解直角三角形:在直角三角形中,由已知元素求未知元素的过程.什么是解直角三角形(2)两锐角之间的关系∠A+∠B=90°(3)边角之间的关系(1)三边之间的关系 (勾股定理)在解直角三角形的过程中,一般要用到下面一些关系:
如何解直角三角形你还有其他方法求出c吗?
如何解直角三角形 根据以上条件可以求出塔身中心线与垂直中心线的夹角.你愿意试着计算一下吗?解决有关比萨斜塔倾斜的问题. 在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 30 , b = 20 ;练习 (2) ∠B=72°,c = 14.名言: 聪明在于学习,天才在于积累。……所谓天才,实际上是依靠学习。_____华罗庚
