(沪教版高二上)数学:第九章 矩阵和行列式初步(章综合)
文档属性
| 名称 | (沪教版高二上)数学:第九章 矩阵和行列式初步(章综合) |

|
|
| 格式 | rar | ||
| 文件大小 | 414.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-20 09:03:00 | ||
图片预览










文档简介
课件39张PPT。第二章 矩阵复习课 主要内容
典型例题
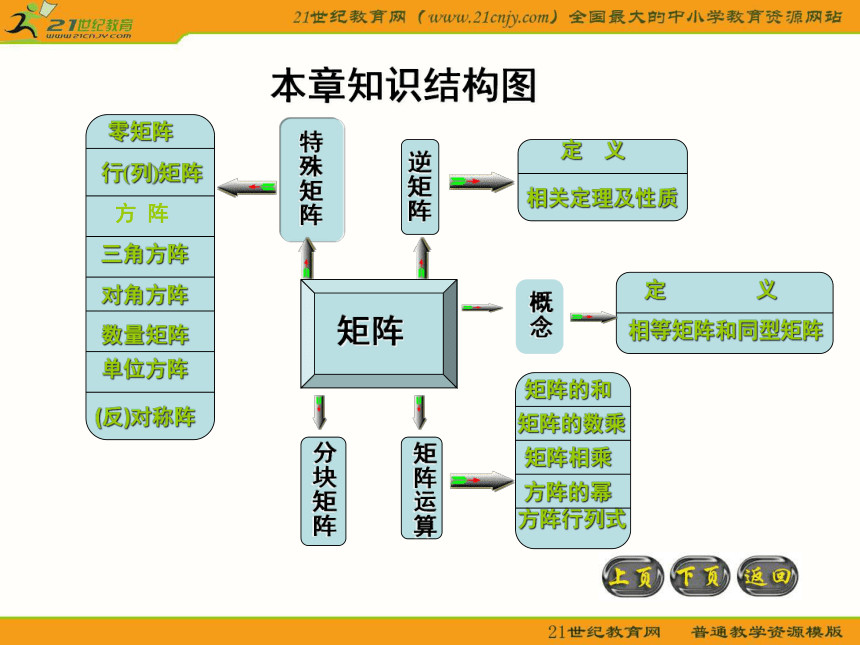
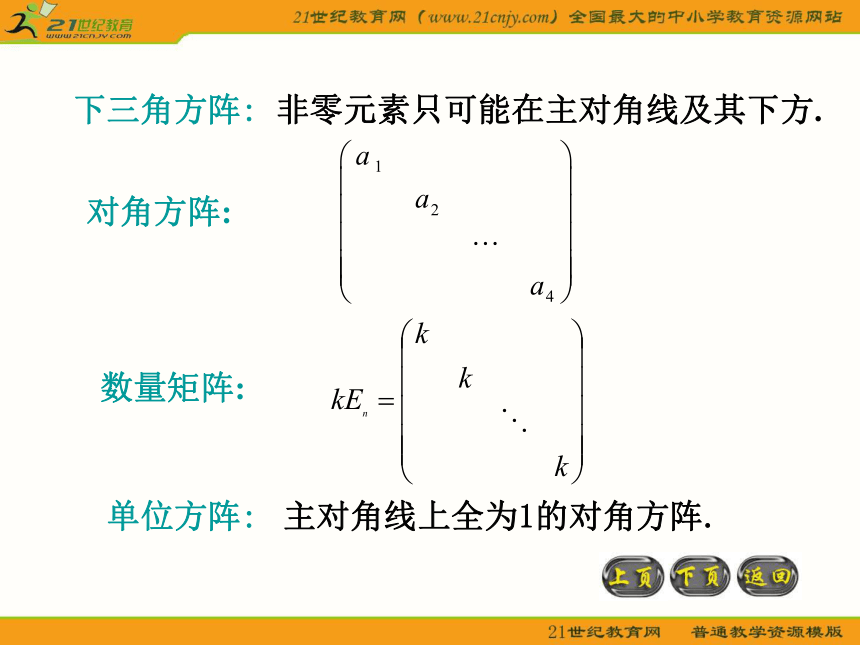
自测题本章知识结构图1 矩阵的定义由 个数排成的 行 列的数表称为矩阵的第i行j列的元素.元素为实数的称为实矩阵,元素为复数的称为复矩阵.2. 几种特殊矩阵元素全为零的 矩阵,记为:O或零矩阵:行矩阵:只有一行的矩阵。 列矩阵:只有一列的矩阵。 方阵:行数列数皆相等的矩阵。上三角方阵: 非零元素只可能在主对角线及其上方。 下三角方阵: 非零元素只可能在主对角线及其下方.对角方阵:数量矩阵:单位方阵: 主对角线上全为1的对角方阵. 3. 矩阵的运算同型矩阵:行数和列数均相等的矩阵.如果两个矩阵 是同型矩阵,且各对应元素也相同,即则称矩阵 相等,记作两个 矩阵 的和矩阵的和:矩阵相等:定义为矩阵的数乘:定义为矩阵的线性运算的运算规律:矩阵相乘:矩阵乘法的运算规律(其中 为数);n阶方阵的幂:若A是 阶矩阵,定义 为A的 次幂, 为正整数,易证转置矩阵:转置矩阵的运算性质对称阵:设 为 阶方阵,如果满足 ,即.则 称为对称阵.反对称阵:伴随方阵:余子式,称方阵为方阵 的伴随方阵.4. 方阵的行列式由 阶方阵 的各元素按原位置排列构成的行列式,叫做方阵 的行列式,记作 或运算性质5. 逆矩阵对于 阶矩阵 ,如果存在 阶矩阵 ,使得则称 为可逆矩阵, 是 的逆方阵。定义 可逆相关定理及性质6. 分块矩阵矩阵的分块,主要目的在于简化运算及便于论证.分块矩阵的运算规则与普通矩阵的运算规则相似.典 型 例 题 一、矩阵的运算
二、有关逆矩阵的运算及证明
三、矩阵方程及其求解方法一、矩阵的运算矩阵运算有其特殊性,若能灵活地运用矩阵的运算性质及运算规律,可极大地提高运算效率.例1注:对一般的 阶方阵 ,我们常常用归纳的方
法求 .例2解:例3若 阶实对称阵 满足 ,证明证: 为对称阵,故有 ,因此有比较 两端的 元素由于 为实数,故 即二、有关逆矩阵的运算及证明1. 利用定义求逆阵利用定义求 阶方阵 逆阵,即找或猜或凑一个 阶方阵 ,使 或 ,从而 .例4例42. 利用伴随矩阵 求逆阵例5注:对2阶数字方阵求逆一般,都用 来做,既简便又迅速,但对3阶及其以上的数字方阵一般不使用 求其逆阵,因为若用 去做,计算工作量太大且容易出错,而是利用下章所介绍的初等变换法.3. 利用分块矩阵求逆阵例6从而4. 利用定义证明某一矩阵 为矩阵 的逆阵例7注:1. 矩阵的逆阵是线性代数中非常重要的一个内容,主要包括:①证明矩阵 可逆;②求逆阵;③证明矩阵 是矩2. 证明矩阵 A 可逆,可利用 A 的行列式不为零或找一个矩阵 B,使 AB=E 或 BA=E 等方法;对数字矩阵,若求其逆阵,一般用 A*(如2阶矩阵)或初等变换(3阶及3阶以上的方阵)的方法来做,有时也利用分块矩阵来做.对抽象的矩阵 A,若求其逆,一般是用定义或 A*来做;证明矩阵 B 是矩阵 A 的逆阵,只需验证 AB=E 或 BA=E 即可. 阵 的逆阵.三. 矩阵方程及其求解方法矩阵方程解例8以及 及 ,再求 及 就麻烦多了. 因此,在求解矩阵方程时,一定要注意先化简方程.例9注:此题若不先化简给出的矩阵方程,而直接求 第二章 自测题一、填空题(8分/题)3) 已知 二. 证明题 (26分)自测题答案1) 3, 1/3, 9, , -1/3; 2) 4;3) 0;一.三.
典型例题
自测题本章知识结构图1 矩阵的定义由 个数排成的 行 列的数表称为矩阵的第i行j列的元素.元素为实数的称为实矩阵,元素为复数的称为复矩阵.2. 几种特殊矩阵元素全为零的 矩阵,记为:O或零矩阵:行矩阵:只有一行的矩阵。 列矩阵:只有一列的矩阵。 方阵:行数列数皆相等的矩阵。上三角方阵: 非零元素只可能在主对角线及其上方。 下三角方阵: 非零元素只可能在主对角线及其下方.对角方阵:数量矩阵:单位方阵: 主对角线上全为1的对角方阵. 3. 矩阵的运算同型矩阵:行数和列数均相等的矩阵.如果两个矩阵 是同型矩阵,且各对应元素也相同,即则称矩阵 相等,记作两个 矩阵 的和矩阵的和:矩阵相等:定义为矩阵的数乘:定义为矩阵的线性运算的运算规律:矩阵相乘:矩阵乘法的运算规律(其中 为数);n阶方阵的幂:若A是 阶矩阵,定义 为A的 次幂, 为正整数,易证转置矩阵:转置矩阵的运算性质对称阵:设 为 阶方阵,如果满足 ,即.则 称为对称阵.反对称阵:伴随方阵:余子式,称方阵为方阵 的伴随方阵.4. 方阵的行列式由 阶方阵 的各元素按原位置排列构成的行列式,叫做方阵 的行列式,记作 或运算性质5. 逆矩阵对于 阶矩阵 ,如果存在 阶矩阵 ,使得则称 为可逆矩阵, 是 的逆方阵。定义 可逆相关定理及性质6. 分块矩阵矩阵的分块,主要目的在于简化运算及便于论证.分块矩阵的运算规则与普通矩阵的运算规则相似.典 型 例 题 一、矩阵的运算
二、有关逆矩阵的运算及证明
三、矩阵方程及其求解方法一、矩阵的运算矩阵运算有其特殊性,若能灵活地运用矩阵的运算性质及运算规律,可极大地提高运算效率.例1注:对一般的 阶方阵 ,我们常常用归纳的方
法求 .例2解:例3若 阶实对称阵 满足 ,证明证: 为对称阵,故有 ,因此有比较 两端的 元素由于 为实数,故 即二、有关逆矩阵的运算及证明1. 利用定义求逆阵利用定义求 阶方阵 逆阵,即找或猜或凑一个 阶方阵 ,使 或 ,从而 .例4例42. 利用伴随矩阵 求逆阵例5注:对2阶数字方阵求逆一般,都用 来做,既简便又迅速,但对3阶及其以上的数字方阵一般不使用 求其逆阵,因为若用 去做,计算工作量太大且容易出错,而是利用下章所介绍的初等变换法.3. 利用分块矩阵求逆阵例6从而4. 利用定义证明某一矩阵 为矩阵 的逆阵例7注:1. 矩阵的逆阵是线性代数中非常重要的一个内容,主要包括:①证明矩阵 可逆;②求逆阵;③证明矩阵 是矩2. 证明矩阵 A 可逆,可利用 A 的行列式不为零或找一个矩阵 B,使 AB=E 或 BA=E 等方法;对数字矩阵,若求其逆阵,一般用 A*(如2阶矩阵)或初等变换(3阶及3阶以上的方阵)的方法来做,有时也利用分块矩阵来做.对抽象的矩阵 A,若求其逆,一般是用定义或 A*来做;证明矩阵 B 是矩阵 A 的逆阵,只需验证 AB=E 或 BA=E 即可. 阵 的逆阵.三. 矩阵方程及其求解方法矩阵方程解例8以及 及 ,再求 及 就麻烦多了. 因此,在求解矩阵方程时,一定要注意先化简方程.例9注:此题若不先化简给出的矩阵方程,而直接求 第二章 自测题一、填空题(8分/题)3) 已知 二. 证明题 (26分)自测题答案1) 3, 1/3, 9, , -1/3; 2) 4;3) 0;一.三.
