直线和圆的位置关系
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
静海实验中学导学案
年级:九年级 学科:数学 主备:杨成霞 审核:九年级数学组
课题:20.2.2直线和圆的位置关系(2) 课型:新课 授课时间:2010——2011(一)第四周
【学习重点】:
直线的判定和性质.
【学习难点】
直线的判定和性质的应用.
【导学过程】
一、知识回顾:
请用“ ”写出直线和圆的位置关系
二、探究新知
(一)切线的判定
1.思考:如图在⊙O中经过半径OA的外端点A做直线l⊥OA,则圆心O到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系
距离是:
位置关系是: ,理由:
2.切线的判定定理:
.
例1 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证直线AB是⊙O的切线.
4.练习:
(1)过圆外一点P画圆的切线.
(2)过圆上一点Q画圆的切线.
(3)如图,AB是⊙O的直径,,AT=AB.求证:AT是⊙O的切线.
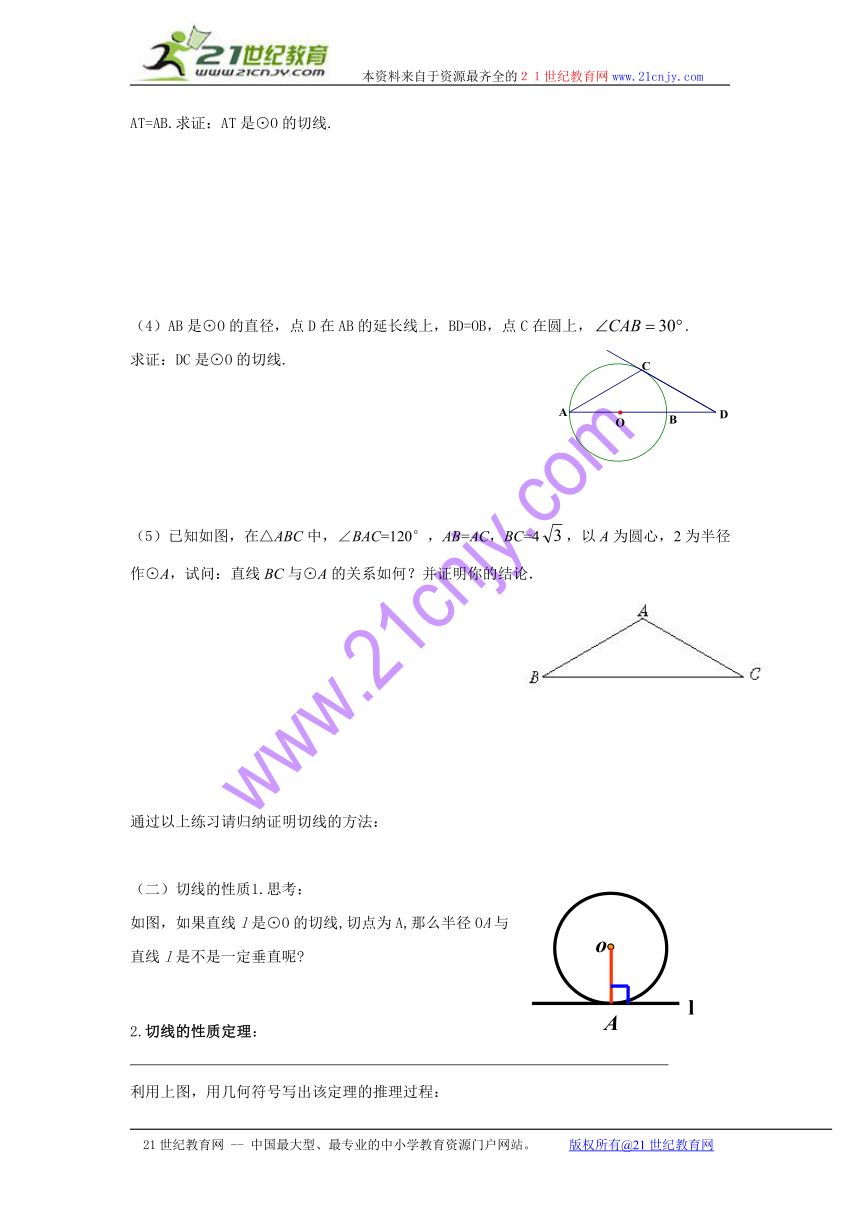
(4)AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,.
求证:DC是⊙O的切线.
(5)已知如图,在△ABC中,∠BAC=120°,AB=AC,BC=4,以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的关系如何?并证明你的结论.
通过以上练习请归纳证明切线的方法:
(二)切线的性质
1.思考:
如图,如果直线l是⊙O的切线,切点为A,那么半径OA与
直线l是不是一定垂直呢
2.切线的性质定理:
利用上图,用几何符号写出该定理的推理过程:
例2 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
3.练习:
(1)如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的
切线,C为切点. 求证:C是AB的中点.
(2)如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延
长线交于点C,且AD=DC,求∠ABD的度数.
自我检测:
1.若AB是⊙O的弦,直线CD切⊙O于点E且CD∥AB,则与的大小关系是______.
2.两个同心圆的半径分别为3 cm和4 cm ,大圆的弦BC与小圆相切,则BC=______ cm.
3.在直径为8 cm的圆外有一点P,点P到圆上的点的最短距离为4 cm,则过点P的圆切线长为______ cm.
4.下列四个命题正确的是:
①与圆有公共点的直线是切线;②垂直于圆的半径的直线是切线;③到圆心的距离等于半径的直线是切线;④过圆直径的端点,垂直于此直径的直线是切线
A.①② B.②③ C.③④ D.①④
5.已知OA平分∠BOC,P是OA上任意一点,如果以P为圆心的圆与OC相离,那么OP与OB的位置关系是
A.相离 B.相切 C.相交 D.不能确定
6.已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.
7.如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E.
求证:CD与小圆相切.
A
l
o
A
l
o
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
静海实验中学导学案
年级:九年级 学科:数学 主备:杨成霞 审核:九年级数学组
课题:20.2.2直线和圆的位置关系(2) 课型:新课 授课时间:2010——2011(一)第四周
【学习重点】:
直线的判定和性质.
【学习难点】
直线的判定和性质的应用.
【导学过程】
一、知识回顾:
请用“ ”写出直线和圆的位置关系
二、探究新知
(一)切线的判定
1.思考:如图在⊙O中经过半径OA的外端点A做直线l⊥OA,则圆心O到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系
距离是:
位置关系是: ,理由:
2.切线的判定定理:
.
例1 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证直线AB是⊙O的切线.
4.练习:
(1)过圆外一点P画圆的切线.
(2)过圆上一点Q画圆的切线.
(3)如图,AB是⊙O的直径,,AT=AB.求证:AT是⊙O的切线.
(4)AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,.
求证:DC是⊙O的切线.
(5)已知如图,在△ABC中,∠BAC=120°,AB=AC,BC=4,以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的关系如何?并证明你的结论.
通过以上练习请归纳证明切线的方法:
(二)切线的性质
1.思考:
如图,如果直线l是⊙O的切线,切点为A,那么半径OA与
直线l是不是一定垂直呢
2.切线的性质定理:
利用上图,用几何符号写出该定理的推理过程:
例2 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
3.练习:
(1)如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的
切线,C为切点. 求证:C是AB的中点.
(2)如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延
长线交于点C,且AD=DC,求∠ABD的度数.
自我检测:
1.若AB是⊙O的弦,直线CD切⊙O于点E且CD∥AB,则与的大小关系是______.
2.两个同心圆的半径分别为3 cm和4 cm ,大圆的弦BC与小圆相切,则BC=______ cm.
3.在直径为8 cm的圆外有一点P,点P到圆上的点的最短距离为4 cm,则过点P的圆切线长为______ cm.
4.下列四个命题正确的是:
①与圆有公共点的直线是切线;②垂直于圆的半径的直线是切线;③到圆心的距离等于半径的直线是切线;④过圆直径的端点,垂直于此直径的直线是切线
A.①② B.②③ C.③④ D.①④
5.已知OA平分∠BOC,P是OA上任意一点,如果以P为圆心的圆与OC相离,那么OP与OB的位置关系是
A.相离 B.相切 C.相交 D.不能确定
6.已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.
7.如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E.
求证:CD与小圆相切.
A
l
o
A
l
o
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
