轴对称(第2、3课时)
图片预览


文档简介
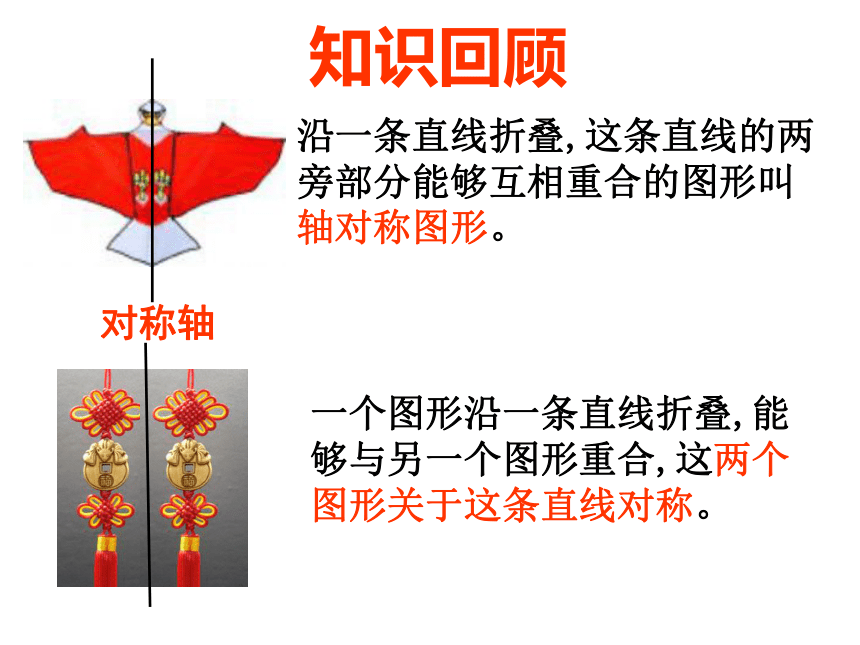
课件23张PPT。12.1轴对称(2)知识回顾 沿一条直线折叠,这条直线的两
旁部分能够互相重合的图形叫
轴对称图形。一个图形沿一条直线折叠,能
够与另一个图形重合,这两个
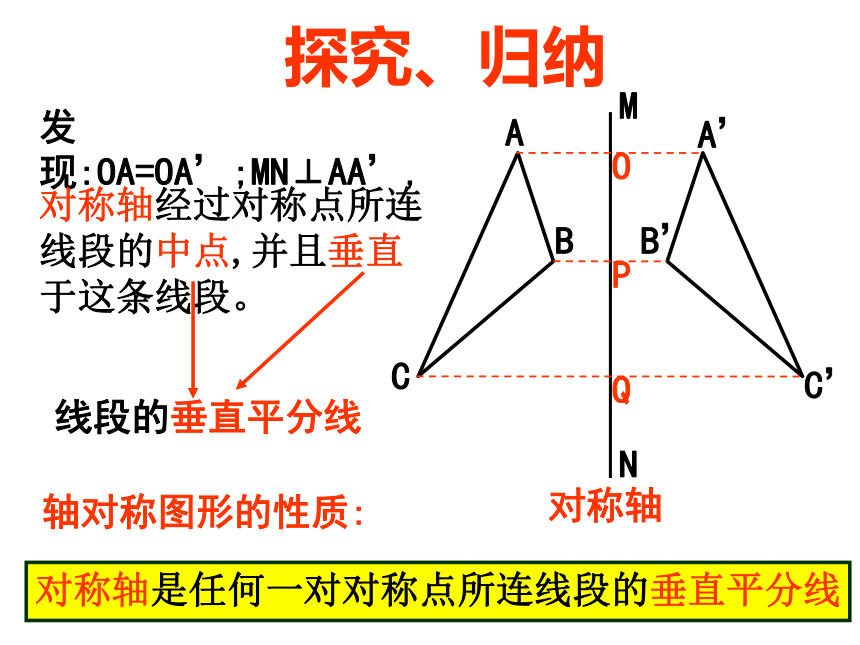
图形关于这条直线对称。对称轴探究、归纳发现:OA=OA’;MN⊥AA’,OPQ对称轴经过对称点所连
线段的中点,并且垂直
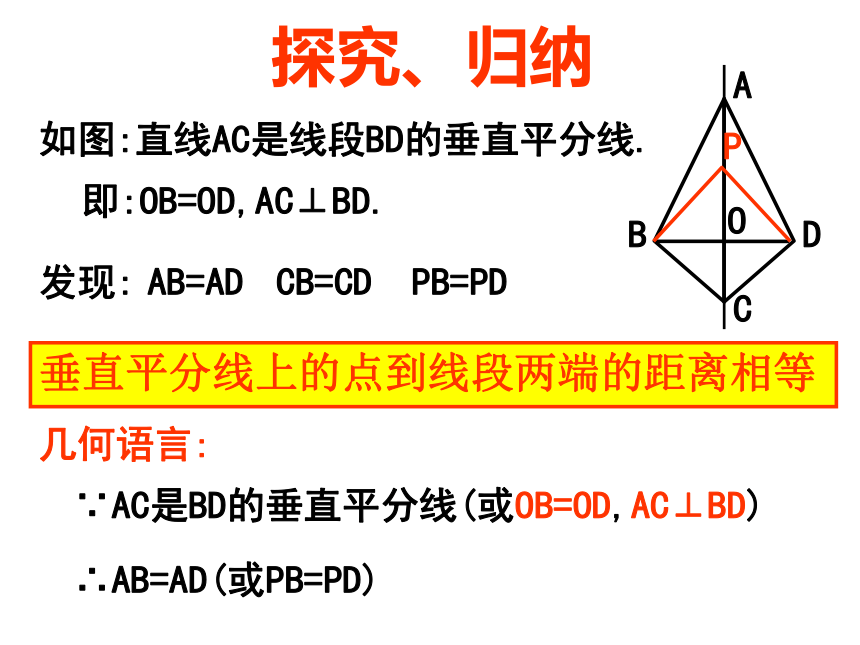
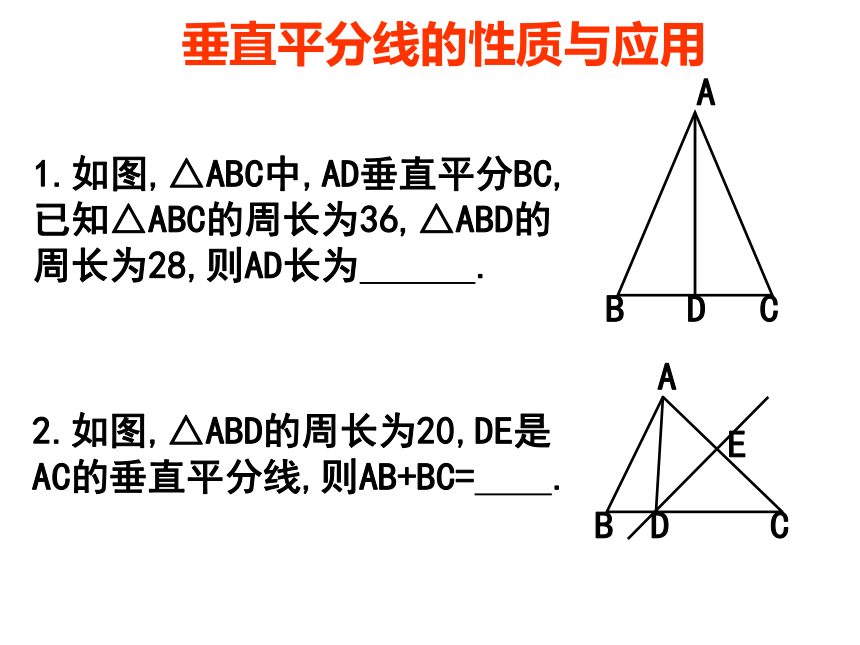
于这条线段。轴对称图形的性质:对称轴是任何一对对称点所连线段的垂直平分线探究、归纳如图:直线AC是线段BD的垂直平分线.垂直平分线上的点到线段两端的距离相等即:OB=OD,AC⊥BD.发现:AB=ADCB=CDPPB=PD几何语言:∵AC是BD的垂直平分线(或OB=OD,AC⊥BD)∴AB=AD(或PB=PD)垂直平分线的性质与应用1.如图,△ABC中,AD垂直平分BC,
已知△ABC的周长为36,△ABD的
周长为28,则AD长为 .2.如图,△ABD的周长为20,DE是
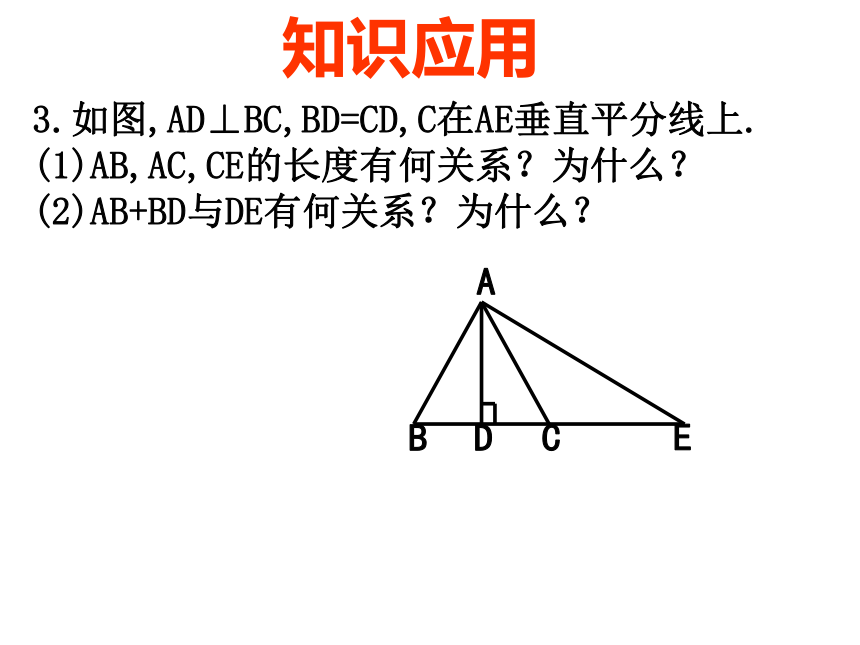
AC的垂直平分线,则AB+BC= .3.如图,AD⊥BC,BD=CD,C在AE垂直平分线上.
(1)AB,AC,CE的长度有何关系?为什么?
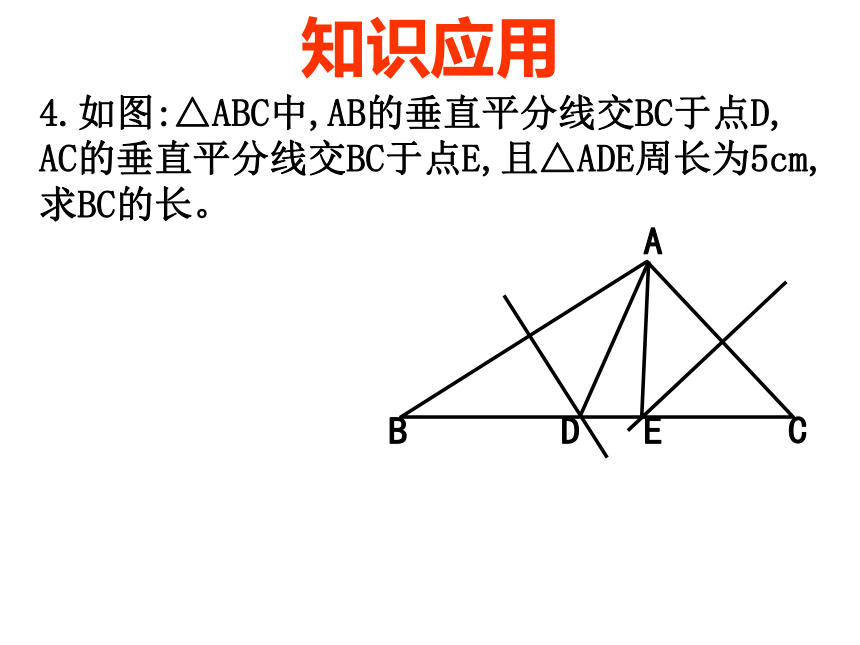
(2)AB+BD与DE有何关系?为什么?知识应用知识应用4.如图:△ABC中,AB的垂直平分线交BC于点D,
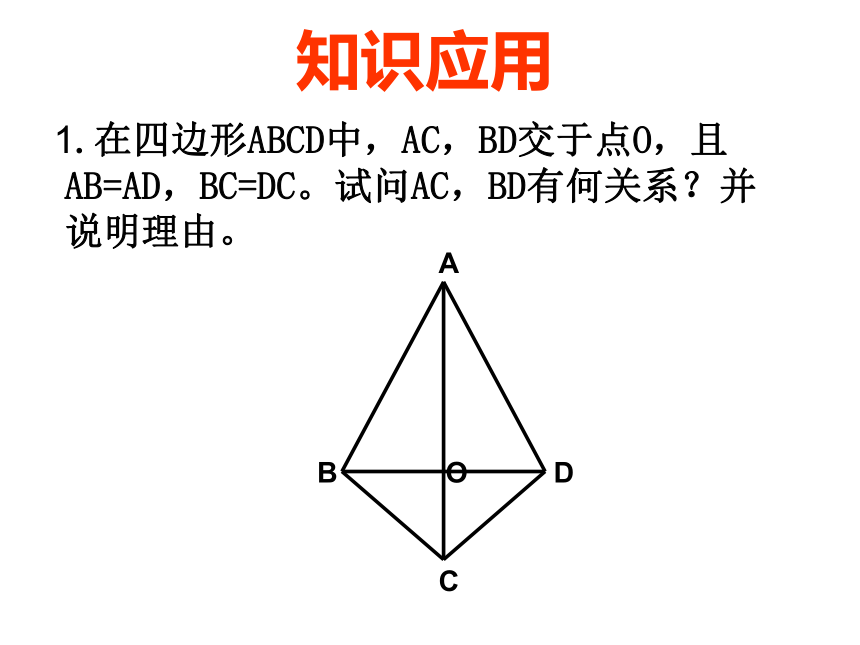
AC的垂直平分线交BC于点E,且△ADE周长为5cm, 求BC的长。探究、归纳已知如图:在⊿PAB中,PA=PB,那么点P在线段AB的垂直平分线上吗?ABP到线段两端的距离相等的点在线段的垂直平分线上几何语言:∵PA=PB∴点P在AB的垂直平分线上∴PO是AB的垂直平分线O证明:过点P作⊿PAB的中线 1.在四边形ABCD中,AC,BD交于点O,且AB=AD,BC=DC。试问AC,BD有何关系?并说明理由。知识应用DABCO2.在⊿ABC中,PD,PE分别是AB,AC的垂直平分线,并相交于点P,求证:点P也在BC的垂直平分线上。知识应用PDEABC垂直平分线的性质与应用3.下列说法错误的是( )
A.点D,E在线段AB垂直平分线上,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是AB的垂直平分线D12.1轴对称(3)知识回顾发现:OA=OA’;MN⊥AA’,OPQ对称轴经过对称点所连
线段的中点,并且垂直
于这条线段.轴对称图形的性质:对称轴是任何一对对称点所连线段的垂直平分线.知识回顾如图:直线AC是线段BD的垂直平分线.垂直平分线上的点到线段两端的距离相等即:OB=OD,AC⊥BD.发现:AB=ADCB=CDPPB=PD几何语言:∵AC是BD的垂直平分线(或OB=OD,AC⊥BD)∴AB=AD(或PB=PD)知识回顾AOBP到线段两端的距离相等的
点在线段的垂直平分线上几何语言:∵PA=PB∴点P在AB的垂直平分线上∴PO是AB的垂直平分线知识应用1.如图:AB=AE,BC=ED,点A在CD的垂直平分线上.
求证:∠B=∠E.变式.如图:AB=AE,BC=ED,∠B=∠E,
且点F是CD的中点.
求证:AF⊥CD.F知识应用3.如图:奶牛养殖场外有一条街道MN,现欲在街道上建一个牛奶供应站O,使其到两个村庄P,Q
的距离相等.MNPQO垂直平分线的性质与应用周长专题3.如图,△ABC中,AB的垂直平分
线交AC于点E,△ABC和△BEC的
周长分别为24和14,则AB= .分段,变换AB+CE+BE=14AB+CE+AE=14AB+BC+CE+AE=24AB=10垂直平分线的性质与应用周长专题4.如图,△ABC中,AB的垂直平分
线交AC于点D,若AC=5,BC=4,
则△BCD的周长= .分段,变换BC+CD+BD=4+CD+AD=4+AC=95.如图,AB比AC长2cm,DE垂直平分BC,△ACD周长为14cm,
则AB= ,AC= .AD+CD+AC=14AB+AC=14AB-AC=2垂直平分线的性质与应用周长专题分段,变换6.如图,△ABC中,∠C=90o,AC=BC,AD平分∠BAC,
DE⊥AB,若AB=12cm,则△BDE的周长是 .引申到角平分线上垂直平分线与角平分线1.如图,A,B,C三个村庄之间有三条公路,现在要
建一个小型菜场P.使得它到三条公路的距离相等使得它到三个村庄的距离相等垂直平分线与角平分线2.电信部门要建一个电视信号塔P,要求到两条公
路的距离相等,同时到两个村庄的距离也相等.垂直平分线与角平分线3.如图,EF⊥AB于点F,EG⊥AC于点G.(1)已知:AE平分∠BAC,DE垂直平分BC.
求证:BF=CG.(2)已知:DE垂直平分BC,BF=CG.
求证:AE平分∠BAC.(3)已知:AE平分∠BAC,
BF=CG,BD=CD.
求证:DE⊥BC.
旁部分能够互相重合的图形叫
轴对称图形。一个图形沿一条直线折叠,能
够与另一个图形重合,这两个
图形关于这条直线对称。对称轴探究、归纳发现:OA=OA’;MN⊥AA’,OPQ对称轴经过对称点所连
线段的中点,并且垂直
于这条线段。轴对称图形的性质:对称轴是任何一对对称点所连线段的垂直平分线探究、归纳如图:直线AC是线段BD的垂直平分线.垂直平分线上的点到线段两端的距离相等即:OB=OD,AC⊥BD.发现:AB=ADCB=CDPPB=PD几何语言:∵AC是BD的垂直平分线(或OB=OD,AC⊥BD)∴AB=AD(或PB=PD)垂直平分线的性质与应用1.如图,△ABC中,AD垂直平分BC,
已知△ABC的周长为36,△ABD的
周长为28,则AD长为 .2.如图,△ABD的周长为20,DE是
AC的垂直平分线,则AB+BC= .3.如图,AD⊥BC,BD=CD,C在AE垂直平分线上.
(1)AB,AC,CE的长度有何关系?为什么?
(2)AB+BD与DE有何关系?为什么?知识应用知识应用4.如图:△ABC中,AB的垂直平分线交BC于点D,
AC的垂直平分线交BC于点E,且△ADE周长为5cm, 求BC的长。探究、归纳已知如图:在⊿PAB中,PA=PB,那么点P在线段AB的垂直平分线上吗?ABP到线段两端的距离相等的点在线段的垂直平分线上几何语言:∵PA=PB∴点P在AB的垂直平分线上∴PO是AB的垂直平分线O证明:过点P作⊿PAB的中线 1.在四边形ABCD中,AC,BD交于点O,且AB=AD,BC=DC。试问AC,BD有何关系?并说明理由。知识应用DABCO2.在⊿ABC中,PD,PE分别是AB,AC的垂直平分线,并相交于点P,求证:点P也在BC的垂直平分线上。知识应用PDEABC垂直平分线的性质与应用3.下列说法错误的是( )
A.点D,E在线段AB垂直平分线上,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是AB的垂直平分线D12.1轴对称(3)知识回顾发现:OA=OA’;MN⊥AA’,OPQ对称轴经过对称点所连
线段的中点,并且垂直
于这条线段.轴对称图形的性质:对称轴是任何一对对称点所连线段的垂直平分线.知识回顾如图:直线AC是线段BD的垂直平分线.垂直平分线上的点到线段两端的距离相等即:OB=OD,AC⊥BD.发现:AB=ADCB=CDPPB=PD几何语言:∵AC是BD的垂直平分线(或OB=OD,AC⊥BD)∴AB=AD(或PB=PD)知识回顾AOBP到线段两端的距离相等的
点在线段的垂直平分线上几何语言:∵PA=PB∴点P在AB的垂直平分线上∴PO是AB的垂直平分线知识应用1.如图:AB=AE,BC=ED,点A在CD的垂直平分线上.
求证:∠B=∠E.变式.如图:AB=AE,BC=ED,∠B=∠E,
且点F是CD的中点.
求证:AF⊥CD.F知识应用3.如图:奶牛养殖场外有一条街道MN,现欲在街道上建一个牛奶供应站O,使其到两个村庄P,Q
的距离相等.MNPQO垂直平分线的性质与应用周长专题3.如图,△ABC中,AB的垂直平分
线交AC于点E,△ABC和△BEC的
周长分别为24和14,则AB= .分段,变换AB+CE+BE=14AB+CE+AE=14AB+BC+CE+AE=24AB=10垂直平分线的性质与应用周长专题4.如图,△ABC中,AB的垂直平分
线交AC于点D,若AC=5,BC=4,
则△BCD的周长= .分段,变换BC+CD+BD=4+CD+AD=4+AC=95.如图,AB比AC长2cm,DE垂直平分BC,△ACD周长为14cm,
则AB= ,AC= .AD+CD+AC=14AB+AC=14AB-AC=2垂直平分线的性质与应用周长专题分段,变换6.如图,△ABC中,∠C=90o,AC=BC,AD平分∠BAC,
DE⊥AB,若AB=12cm,则△BDE的周长是 .引申到角平分线上垂直平分线与角平分线1.如图,A,B,C三个村庄之间有三条公路,现在要
建一个小型菜场P.使得它到三条公路的距离相等使得它到三个村庄的距离相等垂直平分线与角平分线2.电信部门要建一个电视信号塔P,要求到两条公
路的距离相等,同时到两个村庄的距离也相等.垂直平分线与角平分线3.如图,EF⊥AB于点F,EG⊥AC于点G.(1)已知:AE平分∠BAC,DE垂直平分BC.
求证:BF=CG.(2)已知:DE垂直平分BC,BF=CG.
求证:AE平分∠BAC.(3)已知:AE平分∠BAC,
BF=CG,BD=CD.
求证:DE⊥BC.
