11.2 三角形全等的判定学案
文档属性
| 名称 | 11.2 三角形全等的判定学案 |
|
|
| 格式 | rar | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 00:00:00 | ||
图片预览

文档简介
姓名 学习改变命运 思考造就未来 十堰外国语学校 初中数学(人教版)学案 八年级(上) 2009年9月3日
11.2 三角形全等的判定
【学习目标】
1. 掌握全等三角形的判定方法“SAS” .
2. 能灵活运用“SAS”解决线段或角相等.
3. 熟练掌握尺规作图“已知两边及其夹角求作三角形”.
【学习重点】
全等三角形的判定方法“SAS”.
【自学检测】
课本:P15-17习题11.2
3. 4.
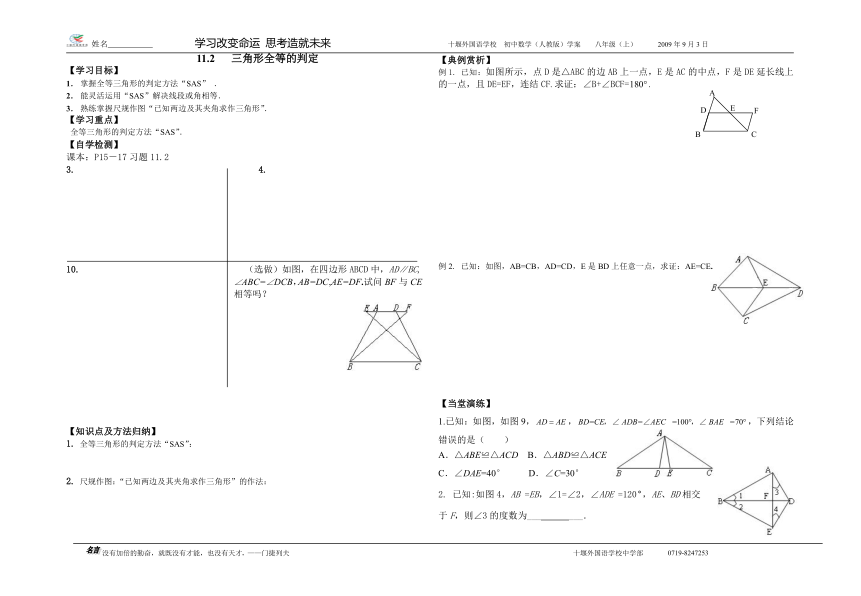
10. (选做)如图,在四边形ABCD中,AD∥BC,
∠ABC=∠DCB,AB=DC,AE=DF.试问BF与CE 相等吗?
【知识点及方法归纳】
1. 全等三角形的判定方法“SAS”:
2. 尺规作图:“已知两边及其夹角求作三角形”的作法:
【典例赏析】
例1. 已知:如图所示,点D是△ABC的边AB上一点,E是AC的中点,F是DE延长线上的一点,且DE=EF,连结CF.求证:∠B+∠BCF=.
例2. 已知:如图,AB=CB,AD=CD,E是BD上任意一点,求证:AE=CE.
【当堂演练】
1.已知:如图,如图9,,,下列结论错误的是( )
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠DAE=40° D.∠C=30°
2. 已知:如图4,AB =EB,∠1=∠2,∠ADE =120°,AE、BD相交
于F,则∠3的度数为___ ___.
【课后巩固】
1.如图, AD是的中线,E,F分别是AD和AD延长线上的点,且,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.地基在同一水平面上,高度相同的两幢楼上分别住着甲、乙两位同学,有一天,甲对乙说:“从我住的这幢楼的底部到你住的那幢楼的顶部的直线距离,等于从你住的那幢楼的底部到我住的这幢楼的顶部的直线距离.”你认为甲的话正确吗?答: .
3.如图,△DAC和△EBC均是等边三角形,AE、BD分别与
CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;
②CM=CN;③AC=DN.其中正确结论的个数是 .
4.如图,AB=AC,AD=AE,求证:BE=CD.
5.如图,AB=AC,AD=AE, ∠1=∠2.求证:∠B=∠C.
【拓展延伸】
1.因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺.请你设计一种方案,粗略测出A、B两杆之间的距离.
2.如图所示,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
3.我们知“有两边和其中一边的对角对应相等的两个三角形不一定全等”.现在把条件略做变动会怎样呢?
(1)有两边和其中一边的对角(该角为锐角)对应相等的两个三角形全等吗?
(2)有两边和其中一边的对角(该角为直角)对应相等的两个三角形全等吗?
(3)有两边和其中一边的对角(该角为钝角)对应相等的两个三角形全等吗?
E
F
C
F
E
B
C
D
A
B
D
A
D
P
E
C
B
A
没有加倍的勤奋,就既没有才能,也没有天才. ——门捷列夫 十堰外国语学校中学部 0719-8247253
11.2 三角形全等的判定
【学习目标】
1. 掌握全等三角形的判定方法“SAS” .
2. 能灵活运用“SAS”解决线段或角相等.
3. 熟练掌握尺规作图“已知两边及其夹角求作三角形”.
【学习重点】
全等三角形的判定方法“SAS”.
【自学检测】
课本:P15-17习题11.2
3. 4.
10. (选做)如图,在四边形ABCD中,AD∥BC,
∠ABC=∠DCB,AB=DC,AE=DF.试问BF与CE 相等吗?
【知识点及方法归纳】
1. 全等三角形的判定方法“SAS”:
2. 尺规作图:“已知两边及其夹角求作三角形”的作法:
【典例赏析】
例1. 已知:如图所示,点D是△ABC的边AB上一点,E是AC的中点,F是DE延长线上的一点,且DE=EF,连结CF.求证:∠B+∠BCF=.
例2. 已知:如图,AB=CB,AD=CD,E是BD上任意一点,求证:AE=CE.
【当堂演练】
1.已知:如图,如图9,,,下列结论错误的是( )
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠DAE=40° D.∠C=30°
2. 已知:如图4,AB =EB,∠1=∠2,∠ADE =120°,AE、BD相交
于F,则∠3的度数为___ ___.
【课后巩固】
1.如图, AD是的中线,E,F分别是AD和AD延长线上的点,且,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.地基在同一水平面上,高度相同的两幢楼上分别住着甲、乙两位同学,有一天,甲对乙说:“从我住的这幢楼的底部到你住的那幢楼的顶部的直线距离,等于从你住的那幢楼的底部到我住的这幢楼的顶部的直线距离.”你认为甲的话正确吗?答: .
3.如图,△DAC和△EBC均是等边三角形,AE、BD分别与
CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;
②CM=CN;③AC=DN.其中正确结论的个数是 .
4.如图,AB=AC,AD=AE,求证:BE=CD.
5.如图,AB=AC,AD=AE, ∠1=∠2.求证:∠B=∠C.
【拓展延伸】
1.因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺.请你设计一种方案,粗略测出A、B两杆之间的距离.
2.如图所示,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
3.我们知“有两边和其中一边的对角对应相等的两个三角形不一定全等”.现在把条件略做变动会怎样呢?
(1)有两边和其中一边的对角(该角为锐角)对应相等的两个三角形全等吗?
(2)有两边和其中一边的对角(该角为直角)对应相等的两个三角形全等吗?
(3)有两边和其中一边的对角(该角为钝角)对应相等的两个三角形全等吗?
E
F
C
F
E
B
C
D
A
B
D
A
D
P
E
C
B
A
没有加倍的勤奋,就既没有才能,也没有天才. ——门捷列夫 十堰外国语学校中学部 0719-8247253
